Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-12
第3章 3D空間の基礎
$§$3-12 行列によるスケール
本節では3D空間内の点、あるいはオブジェクトに対してスケール変換(拡大縮小変換)を実行することについて見ていくが、まず始めにスケールに関しての重要な取り決めについて述べておかなければならない。
2D空間の章では触れてこなかったが、この講義ではスケールに関して次の取り決めに従っている。
(1) 非一様スケール(各軸の倍率が異なるスケール)を実行する場合は、変換の合成において一番初めに実行し、それ以降では非一様スケールは実行しないものとする
(2) 倍率が$0$以下のスケール(倍率が$0$あるいはマイナスの値をとるスケール)は実行しない
ただし、一様スケール(各軸の倍率が同じスケール ; 倍率はプラスの値)については、変換の合成における順番はどこでもよく、何度使っても構わない。
\begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\0 &0 &s_z &0 \\0 &0 &0 &1 \end{pmatrix}例えば、3D空間の点$(a, b, c)$を、x軸方向に$s_x$倍、y軸方向に$s_y$倍、z軸方向に$s_z$倍させる計算は次のように行われる。\[\begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\0 &0 &s_z &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}a \\b \\c \\1 \end{pmatrix}=\begin{pmatrix}s_{x}a \\s_{y}b \\s_{z}c \\1\end{pmatrix}\]すなわち、x座標を$s_x$倍、y座標を$s_y$倍、z座標を$s_z$倍させた結果になる。
このように、3D空間上のスケール行列を作成するためには、x軸方向の倍率$s_x$、y軸方向の倍率$s_y$、z軸方向の倍率$s_z$ の3つのデータを指定する必要がある (プログラムにおいて使用してきたVector3構造体は3つの数値を保持できるので、スケール行列を作成する際にはVector3インスタンスが1つあればよい)。
では実際に、3D空間内のいくつかの点に対してスケールを実行しよう。
まず、点$R=(4, 3, 2)$を各軸方向に$2$倍拡大する。各軸方向に$2$倍の拡大を実行するスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}4 \\3 \\2 \\1\end{pmatrix}=\begin{pmatrix}2 &0 &0 &0 \\0 &2 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}4 \\3 \\2 \\1\end{pmatrix}=\begin{pmatrix}8 \\6 \\4 \\1\end{pmatrix}\]
図1、図2はスケール実行前、実行後における点$R$である。各軸方向に$2$倍拡大されるので、実行後の点$R$のx座標、y座標、z座標はいずれも$2$倍の値になっている。
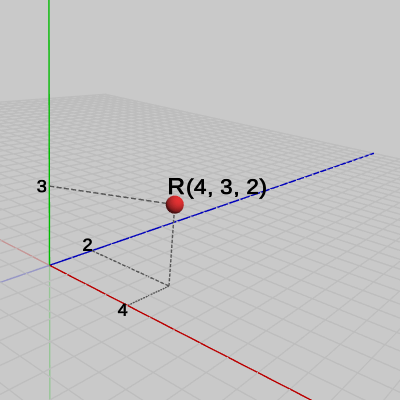
図1 スケール実行前の点R(4, 3, 2) 
図2 スケール実行後の点R(8, 6, 4)
次に、点$G=(3, 3, -8)$をy軸方向にのみ$3$倍拡大する。この場合のスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}3 \\3 \\-8 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &0 \\0 &3 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}3 \\3 \\-8 \\1\end{pmatrix}=\begin{pmatrix}3 \\9 \\-8 \\1\end{pmatrix}\]
図3、図4はスケール実行前、実行後における点$G$である。y軸方向にのみ$3$倍拡大されるので、実行後の点$G$のy座標のみが$3$倍の値になっている。
図3 スケール実行前の点G(3, 3, -8) 
図4 スケール実行後の点G(3, 9, -8)
次に、点$B=(-8, 5, -4)$をx軸方向に$0.5$倍縮小、z軸方向に$1.5$倍拡大する。この場合のスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}-8 \\5 \\-4 \\1\end{pmatrix}=\begin{pmatrix}0.5 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1.5 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}-8 \\5 \\-4 \\1\end{pmatrix}=\begin{pmatrix}-4 \\5 \\-6 \\1\end{pmatrix}\]
図5、図6はスケール実行前、実行後における点$B$である。x軸方向に$0.5$倍縮小、z軸方向に$1.5$倍拡大されるので、実行後の点$B$のx座標は$0.5$倍された値になり、z座標は$1.5$倍された値になっている。
図5 スケール実行前の点B(-8, 5, -4) 
図6 スケール実行後の点B(-4, 5, -6)
点$P=(a, b, c)$をx軸方向に$s_x$倍するということは、原点から点$P$までのx軸方向の距離を$s_x$倍するということである。同様に、点$P$をy軸方向に$s_y$倍、z軸方向に$s_z$倍するということは、原点から点$P$までのy軸方向の距離を$s_y$倍し、原点から点$P$までのz軸方向の距離を$s_z$倍するということである。
図7 点P(a, b, c) 
図8 スケール実行後の点P(sxa, syb, szc)
例えば、図7における点$P$の座標は$(a, b, c)$であるが、これは原点から点$P$までの距離がx軸方向に$a$、y軸方向に$b$、z軸方向に$c$であることを意味する。したがって、x軸方向に$s_x$倍すると、原点から点$P$までのx軸方向の距離が$s_x$倍され、点$P$のx座標は$s_{x}a$となる。同様に、y軸方向に$s_y$倍すると、原点から点$P$までのy軸方向の距離が$s_y$倍され、点$P$のy座標は$s_{y}b$となり、z軸方向に$s_z$倍すると、原点から点$P$までのz軸方向の距離が$s_z$倍され、点$P$のz座標は$s_{z}c$となる (図8)。
図9 Cube 初期状態 図9は一辺の長さが$2$の立方体オブジェクトCubeである。図は Cubeの初期状態であり、その中心が原点に位置している。
Cubeの8個の頂点のうち3つの頂点$v_1$、$v_2$、$v_3$には座標が表示されており、それぞれ $v_1(1,\ 1, -1)$、$v_2(1,\ 1,\ 1)$、$v_3(-1,\ 1, -1)$ である。
ここでは、Cubeに対して以下の3つのスケール行列$S_1$、$S_2$、$S_3$ を実行するが、それぞれの内容は次のとおり。
$S_1$ : x軸、y軸、z軸方向に$3$倍拡大。
$S_2$ : y軸方向にのみ$4$倍拡大。
$S_3$ : x軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小、z軸方向に$3$倍拡大。
オブジェクトに対して実行するスケール行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
また、次のように引数を1つだけ指定することもできる。
実際のプログラムを以下に示す。
以下の図10、図11、図12は初期状態の Cubeにスケール行列$S_1$、$S_2$、$S_3$を実行したときの結果である。
オブジェクトにスケール行列を実行するということは、オブジェクトを構成するすべての頂点のそれぞれにスケール行列を実行することになる。Cubeの場合は8個の頂点で構成されているので、その8個すべての頂点にスケール行列が実行される。
例えば、スケール実行前の3つの頂点$v_1$、$v_2$、$v_3$の座標は $v_1(1,\ 1, -1)$、$v_2(1,\ 1,\ 1)$、$v_3(-1,\ 1, -1)$ であった。スケール実行後においては、$v_1$、$v_2$、$v_3$の座標はそれぞれの軸方向の倍率が掛けられた値になっている (すなわち、原点から各頂点までのx軸方向、y軸方向、z軸方向の距離が指定の倍率分 拡大あるいは縮小された結果になっている)。
それらの行列は次のような形であった (以下の回転行列の各成分$r_{ij}$は3-11節の任意軸回転行列の各成分)。
実際、2つの$4\times4$行列$A$、$B$があり、それらの第4行目が「$0\ 0\ 0\ 1$」であるとする。その積を$C$とすれば、
となり、$C$の第4行目は確かに「$0\ 0\ 0\ 1$」になっている。この$C$に対して、さらに 第4行目が「$0\ 0\ 0\ 1$」である$4\times4$行列を掛けることは上と同様の計算を繰り返すことに等しく、やはり その積の第4行目は「$0\ 0\ 0\ 1$」である。つまり、第4行目が「$0\ 0\ 0\ 1$」である$4\times4$行列を何度掛けても、その積の第4行目は「$0\ 0\ 0\ 1$」なのである。
これは、上に示した3種類の変換行列をどのような順序で何度掛けても、その積の第4行目は「$0\ 0\ 0\ 1$」であることを意味している。
では、本節の内容に関するプログラムを作成する。
$S_1$ : x軸、y軸、z軸方向に$3$倍拡大。
$S_2$ : y軸方向にのみ$4$倍拡大。
$S_3$ : x軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小、z軸方向に$3$倍拡大。
[Code1] (実行結果 図10、図11、図12)
これは上で扱ったプログラムと同じものであり、それぞれの実行結果は図10、図11、図12である。
[Code2] (実行結果 図13)
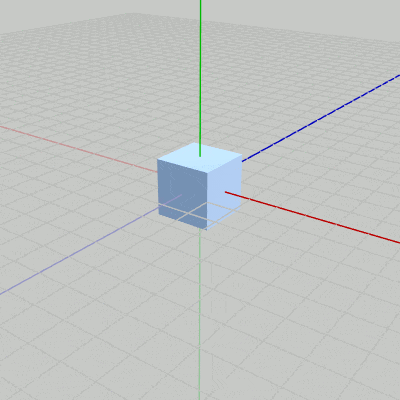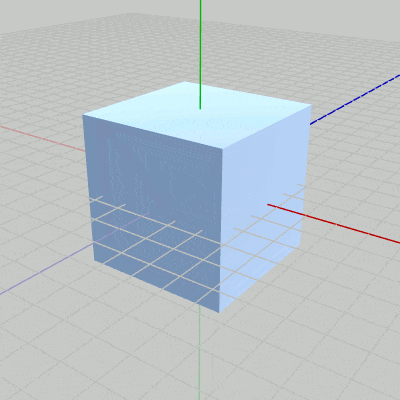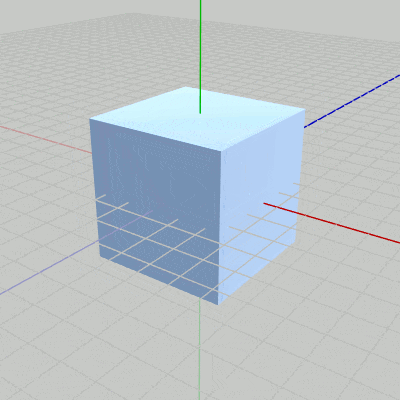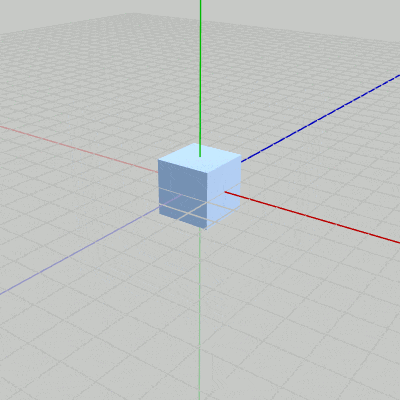
図13 Code2 実行結果 このプログラムは1-10節のCode5とほとんど同じである。
1行目から5行目は単振動による倍率の計算である (単振動に関する解説も1-10節を参照)。5行目で算出される scale は、プログラム実行中に$1$から$3$の間を往復する。この scale倍の拡大を行うスケール行列Sを毎フレーム Cubeに実行することによって、Cubeは実行結果(図13)に見られるような拡大縮小を繰り返すことになる。
2D空間の章では触れてこなかったが、この講義ではスケールに関して次の取り決めに従っている。
(1) 非一様スケール(各軸の倍率が異なるスケール)を実行する場合は、変換の合成において一番初めに実行し、それ以降では非一様スケールは実行しないものとする
(2) 倍率が$0$以下のスケール(倍率が$0$あるいはマイナスの値をとるスケール)は実行しない
ただし、一様スケール(各軸の倍率が同じスケール ; 倍率はプラスの値)については、変換の合成における順番はどこでもよく、何度使っても構わない。
A) 点のスケール
3D空間において、x軸方向に$s_x$倍、y軸方向に$s_y$倍、z軸方向に$s_z$倍のスケールを実行するスケール行列(Scale Matrix)は次のように$3\times3$行列で表される。\begin{pmatrix}s_x &0 &0 \\0 &s_y &0 \\0 &0 &s_z\end{pmatrix}しかし、回転行列の場合もそうであったように、実際に使用する場合には同次座標に対応させるために1次元拡張した次の$4\times4$行列の形のものを使用する。\begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\0 &0 &s_z &0 \\0 &0 &0 &1 \end{pmatrix}例えば、3D空間の点$(a, b, c)$を、x軸方向に$s_x$倍、y軸方向に$s_y$倍、z軸方向に$s_z$倍させる計算は次のように行われる。\[\begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\0 &0 &s_z &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}a \\b \\c \\1 \end{pmatrix}=\begin{pmatrix}s_{x}a \\s_{y}b \\s_{z}c \\1\end{pmatrix}\]すなわち、x座標を$s_x$倍、y座標を$s_y$倍、z座標を$s_z$倍させた結果になる。
このように、3D空間上のスケール行列を作成するためには、x軸方向の倍率$s_x$、y軸方向の倍率$s_y$、z軸方向の倍率$s_z$ の3つのデータを指定する必要がある (プログラムにおいて使用してきたVector3構造体は3つの数値を保持できるので、スケール行列を作成する際にはVector3インスタンスが1つあればよい)。
では実際に、3D空間内のいくつかの点に対してスケールを実行しよう。
まず、点$R=(4, 3, 2)$を各軸方向に$2$倍拡大する。各軸方向に$2$倍の拡大を実行するスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}4 \\3 \\2 \\1\end{pmatrix}=\begin{pmatrix}2 &0 &0 &0 \\0 &2 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}4 \\3 \\2 \\1\end{pmatrix}=\begin{pmatrix}8 \\6 \\4 \\1\end{pmatrix}\]
図1、図2はスケール実行前、実行後における点$R$である。各軸方向に$2$倍拡大されるので、実行後の点$R$のx座標、y座標、z座標はいずれも$2$倍の値になっている。
次に、点$G=(3, 3, -8)$をy軸方向にのみ$3$倍拡大する。この場合のスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}3 \\3 \\-8 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &0 \\0 &3 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}3 \\3 \\-8 \\1\end{pmatrix}=\begin{pmatrix}3 \\9 \\-8 \\1\end{pmatrix}\]
図3、図4はスケール実行前、実行後における点$G$である。y軸方向にのみ$3$倍拡大されるので、実行後の点$G$のy座標のみが$3$倍の値になっている。
次に、点$B=(-8, 5, -4)$をx軸方向に$0.5$倍縮小、z軸方向に$1.5$倍拡大する。この場合のスケール行列を$S$とすれば、スケール実行後の点の座標は次のように求められる。\[S \begin{pmatrix}-8 \\5 \\-4 \\1\end{pmatrix}=\begin{pmatrix}0.5 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1.5 &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}-8 \\5 \\-4 \\1\end{pmatrix}=\begin{pmatrix}-4 \\5 \\-6 \\1\end{pmatrix}\]
図5、図6はスケール実行前、実行後における点$B$である。x軸方向に$0.5$倍縮小、z軸方向に$1.5$倍拡大されるので、実行後の点$B$のx座標は$0.5$倍された値になり、z座標は$1.5$倍された値になっている。
点$P=(a, b, c)$をx軸方向に$s_x$倍するということは、原点から点$P$までのx軸方向の距離を$s_x$倍するということである。同様に、点$P$をy軸方向に$s_y$倍、z軸方向に$s_z$倍するということは、原点から点$P$までのy軸方向の距離を$s_y$倍し、原点から点$P$までのz軸方向の距離を$s_z$倍するということである。
例えば、図7における点$P$の座標は$(a, b, c)$であるが、これは原点から点$P$までの距離がx軸方向に$a$、y軸方向に$b$、z軸方向に$c$であることを意味する。したがって、x軸方向に$s_x$倍すると、原点から点$P$までのx軸方向の距離が$s_x$倍され、点$P$のx座標は$s_{x}a$となる。同様に、y軸方向に$s_y$倍すると、原点から点$P$までのy軸方向の距離が$s_y$倍され、点$P$のy座標は$s_{y}b$となり、z軸方向に$s_z$倍すると、原点から点$P$までのz軸方向の距離が$s_z$倍され、点$P$のz座標は$s_{z}c$となる (図8)。
B) オブジェクトにスケール行列を実行する
Cubeの8個の頂点のうち3つの頂点$v_1$、$v_2$、$v_3$には座標が表示されており、それぞれ $v_1(1,\ 1, -1)$、$v_2(1,\ 1,\ 1)$、$v_3(-1,\ 1, -1)$ である。
ここでは、Cubeに対して以下の3つのスケール行列$S_1$、$S_2$、$S_3$ を実行するが、それぞれの内容は次のとおり。
$S_1$ : x軸、y軸、z軸方向に$3$倍拡大。
$S_2$ : y軸方向にのみ$4$倍拡大。
$S_3$ : x軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小、z軸方向に$3$倍拡大。
\[S_1 =\begin{pmatrix}3 &0 &0 &0 \\0 &3 &0 &0 \\0 &0 &3 &0 \\0 &0 &0 &1 \end{pmatrix}\qquad S_2 =\begin{pmatrix}1 &0 &0 &0 \\0 &4 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix}\qquad S_3 =\begin{pmatrix}2 &0 &0 &0 \\0 &0.5 &0 &0 \\0 &0 &3 &0 \\0 &0 &0 &1 \end{pmatrix}\]
オブジェクトに対して実行するスケール行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
TH3DMath.GetScale4x4(float sx, float sy, float sz)
: 3D空間においてx軸方向に$s_x$倍、y軸方向に$s_y$倍、z軸方向に$s_z$倍の拡大縮小を実行するスケール行列を取得するための TH3DMathクラスの staticメソッドで、戻り値は Matrix4x4型のインスタンス。また、次のように引数を1つだけ指定することもできる。
TH3DMath.GetScale4x4(float s)
: この場合には、x軸方向、y軸方向、z軸方向の倍率はともに$s$倍となる。実際のプログラムを以下に示す。
Matrix4x4 S1 = TH3DMath.GetScale4x4(3.0f); //Matrix4x4 S2 = TH3DMath.GetScale4x4(1.0f, 4.0f, 1.0f); //Matrix4x4 S3 = TH3DMath.GetScale4x4(2.0f, 0.5f, 3.0f); Cube.SetMatrix(S1);
以下の図10、図11、図12は初期状態の Cubeにスケール行列$S_1$、$S_2$、$S_3$を実行したときの結果である。
-
図10 S1(x軸方向、y軸方向、z軸方向に3倍拡大)を実行した場合 -
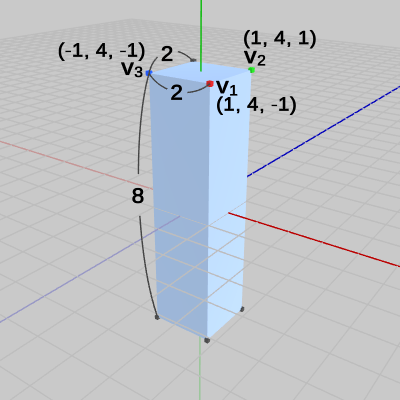図11 S2(y軸方向に4倍拡大)を実行した場合 -
図12 S3(x軸方向に2倍拡大、y軸方向に0.5倍縮小、z軸方向に3倍拡大)を実行した場合
オブジェクトにスケール行列を実行するということは、オブジェクトを構成するすべての頂点のそれぞれにスケール行列を実行することになる。Cubeの場合は8個の頂点で構成されているので、その8個すべての頂点にスケール行列が実行される。
例えば、スケール実行前の3つの頂点$v_1$、$v_2$、$v_3$の座標は $v_1(1,\ 1, -1)$、$v_2(1,\ 1,\ 1)$、$v_3(-1,\ 1, -1)$ であった。スケール実行後においては、$v_1$、$v_2$、$v_3$の座標はそれぞれの軸方向の倍率が掛けられた値になっている (すなわち、原点から各頂点までのx軸方向、y軸方向、z軸方向の距離が指定の倍率分 拡大あるいは縮小された結果になっている)。
C) 補足
3-9節から本節までに3種類の変換行列、すなわち 平行移動行列、回転行列、スケール行列について簡単に解説した。それらの行列は次のような形であった (以下の回転行列の各成分$r_{ij}$は3-11節の任意軸回転行列の各成分)。
\[\begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\qquad\begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix}\qquad\begin{pmatrix}s_x &0 &0 &0\\0 &s_y &0 &0\\0 &0 &s_z &0\\0 &0 &0 &1\end{pmatrix}\]
行列の各成分を見ればわかるように、この3種類の変換行列の第4行目はいずれも「$0\ 0\ 0\ 1$」である。第4行目が「$0\ 0\ 0\ 1$」である$4\times4$行列同士を掛けた場合、その積の第4行目も「$0\ 0\ 0\ 1$」となる。実際、2つの$4\times4$行列$A$、$B$があり、それらの第4行目が「$0\ 0\ 0\ 1$」であるとする。その積を$C$とすれば、
\begin{align*}BA &= \begin{pmatrix}b_{11} &b_{12} &b_{13} &b_{14} \\b_{21} &b_{22} &b_{23} &b_{24} \\b_{31} &b_{32} &b_{33} &b_{34} \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}a_{11} &a_{12} &a_{13} &a_{14} \\a_{21} &a_{22} &a_{23} &a_{24} \\a_{31} &a_{32} &a_{33} &a_{34} \\0 &0 &0 &1 \end{pmatrix} \\\\&= \begin{pmatrix}c_{11} &c_{12} &c_{13} &c_{14} \\c_{21} &c_{22} &c_{23} &c_{24} \\c_{31} &c_{32} &c_{33} &c_{34} \\0\cdot a_{11} + 0\cdot a_{21} + 0\cdot a_{31} + 1\cdot 0 &0\cdot a_{12} + 0\cdot a_{22} + 0\cdot a_{32} + 1\cdot 0 &0\cdot a_{13} + 0\cdot a_{23} + 0\cdot a_{33} + 1\cdot 0 &0\cdot a_{14} + 0\cdot a_{24} + 0\cdot a_{34} + 1\cdot 1 \end{pmatrix} \\\\&= \begin{pmatrix}c_{11} &c_{12} &c_{13} &c_{14} \\c_{21} &c_{22} &c_{23} &c_{24} \\c_{31} &c_{32} &c_{33} &c_{34} \\0 &0 &0 &1 \end{pmatrix}= C\end{align*}
となり、$C$の第4行目は確かに「$0\ 0\ 0\ 1$」になっている。この$C$に対して、さらに 第4行目が「$0\ 0\ 0\ 1$」である$4\times4$行列を掛けることは上と同様の計算を繰り返すことに等しく、やはり その積の第4行目は「$0\ 0\ 0\ 1$」である。つまり、第4行目が「$0\ 0\ 0\ 1$」である$4\times4$行列を何度掛けても、その積の第4行目は「$0\ 0\ 0\ 1$」なのである。
これは、上に示した3種類の変換行列をどのような順序で何度掛けても、その積の第4行目は「$0\ 0\ 0\ 1$」であることを意味している。
では、本節の内容に関するプログラムを作成する。
# Code1
第1のプログラムは Cubeに対して以下の3つのスケール行列を実行するものである。$S_1$ : x軸、y軸、z軸方向に$3$倍拡大。
$S_2$ : y軸方向にのみ$4$倍拡大。
$S_3$ : x軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小、z軸方向に$3$倍拡大。
[Code1] (実行結果 図10、図11、図12)
Matrix4x4 S1 = TH3DMath.GetScale4x4(3.0f); //Matrix4x4 S2 = TH3DMath.GetScale4x4(1.0f, 4.0f, 1.0f); //Matrix4x4 S3 = TH3DMath.GetScale4x4(2.0f, 0.5f, 3.0f); Cube.SetMatrix(S1);
これは上で扱ったプログラムと同じものであり、それぞれの実行結果は図10、図11、図12である。
# Code2
次のプログラムは Cubeを倍率$1$倍から$3$倍の間で拡大縮小させるものである。[Code2] (実行結果 図13)
i_shm += 2; float min = 1.0f; float max = 3.0f; float A = max - min; float scale = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f) + min; Matrix4x4 S = TH3DMath.GetScale4x4(scale); Cube.SetMatrix(S);
1行目から5行目は単振動による倍率の計算である (単振動に関する解説も1-10節を参照)。5行目で算出される scale は、プログラム実行中に$1$から$3$の間を往復する。この scale倍の拡大を行うスケール行列Sを毎フレーム Cubeに実行することによって、Cubeは実行結果(図13)に見られるような拡大縮小を繰り返すことになる。
© 2020-2024 Redpoll's 60 (All rights reserved)