Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-10
第3章 3D空間の基礎
$§$3-10 回転行列 1
2D空間においては、回転行列は角度だけを指定すればよかった。3D空間における回転行列では、角度の他に回転軸というものを指定する必要がある。
本節では3D空間の回転行列のうちx軸、y軸、z軸といった基本的な軸周りの回転を扱う。
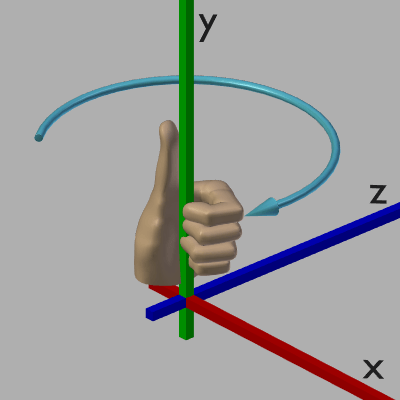
図4 左手系における回転 3-3節「左手系と右手系」においても述べたが、左手系における回転は図4に示されるように、左手の親指を回転軸とみなした場合、残りの指の曲がっている方向が回転のプラス方向(注1)として扱われる(図4ではy軸が回転軸になっている ; x軸、y軸、z軸が回転軸である場合は特に指示がなければ軸の方向は $(1, 0, 0)$、$(0, 1, 0)$、$(0, 0, 1)$である。$(-1, 0, 0)$、$(0, -1, 0)$、$(0, 0, -1)$ではない)。
図1、図3が示すx軸、z軸周りの回転の場合でも、左手の親指を回転軸であるx軸、z軸に合わせれば残りの指の曲がっている方向は、図における水色の回転ベクトルの方向と一致する。
(注1 「回転のプラス方向」とは回転角度を増加させたときに進む方向である。回転角度を減少させれば反対の方向に進む)
3D空間における回転行列(Rotation Matrix)は $3\times3$行列で表すことができる。
x軸、y軸、z軸を回転軸として$\theta$だけ回転させる行列は以下のように表される(左からx軸周り、y軸周り、z軸周りの回転行列)。
例えば、図5の点$P$を図に示される回転軸(淡い赤色のベクトル)の周りで回転させる場合について見ていこう。
点$P$から回転軸へ垂線を下ろし、その足を点$Q$とする(図6 ; ある点から直線へ垂線を下ろすことについては3-4節参照)。このとき点$P$は、垂線の長さを半径とする点$Q$中心の円周上を回転することになる(図7)。回転軸は、図7の円周を含む平面の法線ベクトルになっている。
これが3D空間における回転である。
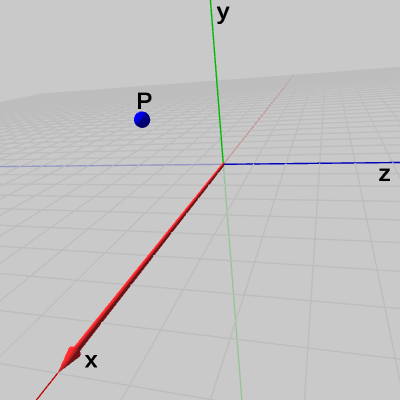
図8 点P 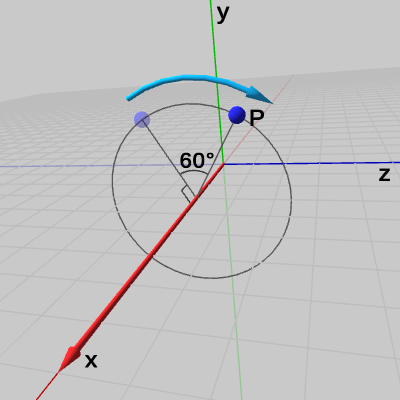
図9 x軸を回転軸として60°回転
両者とも初期状態での位置であり、図10のオブジェクトSignboard1はオブジェクトの底面の中心が原点に置かれており、図11のオブジェクトSignboard2は初期状態でのオブジェクトの底面の中心が$(2,\ 0,\ 1)$に置かれている。
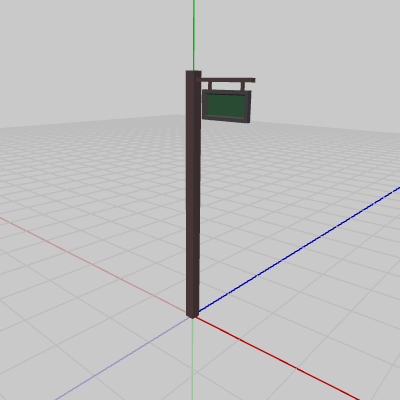
図10 Signboard1 初期状態 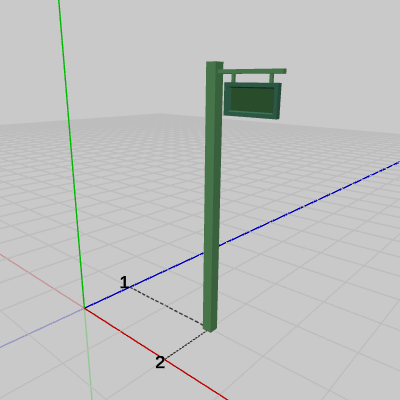
図11 Signboard2 初期状態(底面の中心が原点ではなく(2, 0, 1))
(3D空間での)回転行列を取得するにあたっては、カスタムライブラリーの次のメソッドを使用する。
axisを回転軸として角度degだけ回転させる行列を取得する (戻り値は Matrix4x4型)。
次のプログラムは、y軸を回転軸とする回転行列を取得し、オブジェクトに実行する処理である。回転角度を表すインスタンス変数i_degRotは毎フレーム$1$°ずつ増加するので、オブジェクトも毎フレーム$1$°ずつ回転する。
回転軸に指定されているVector3.upは、Unityに標準で用意されている定数で$(0, 1, 0)$、すなわちy軸のプラス方向を表す。
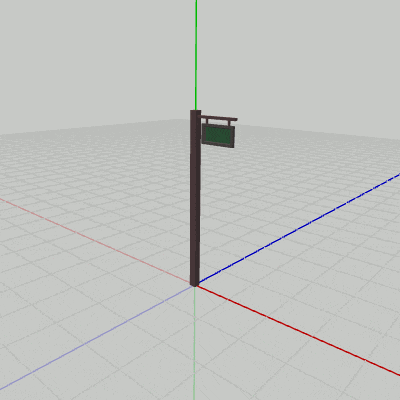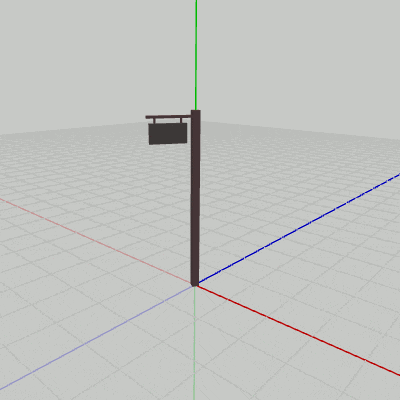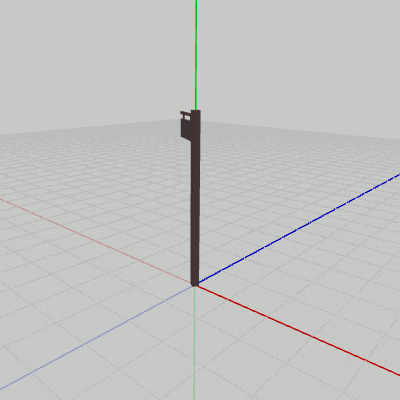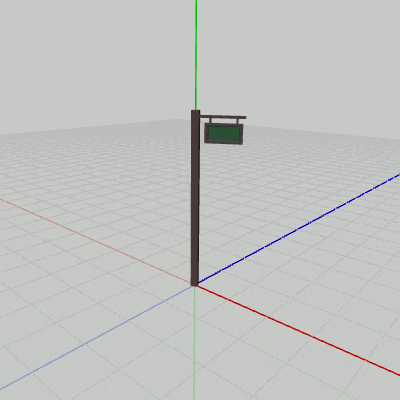
図12 Signboard1の回転 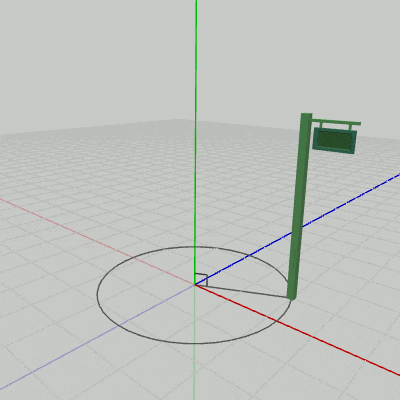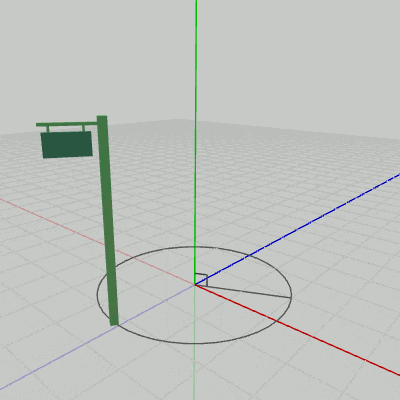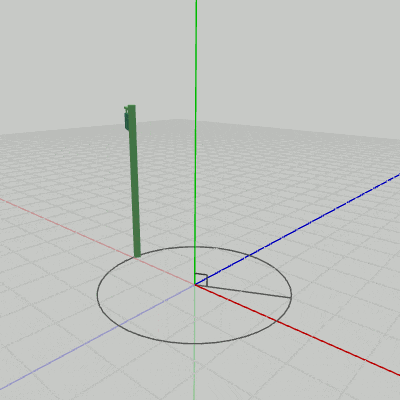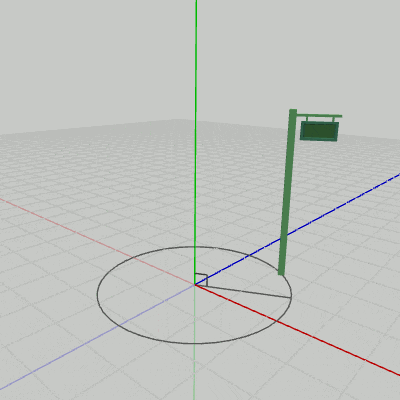
図13 Signboard2の回転
Signboard1は(初期状態において)オブジェクト自体に、回転軸であるy軸が貫通しているので、このプログラムを実行すると図12のような結果になる。Signboard2の場合は、初期状態の位置が回転軸であるy軸から離れた位置にあるため、y軸周りの回転では図13のような結果になる。Signboard2は初期状態では底面の中心が$(2, 0, 1)$に置かれていたが、そのために$(2, 0, 1)$からy軸へ下ろした垂線を半径とする円周上をSignboard2は回転することになる。
オブジェクトを回転させることは、より正確にいえばそのオブジェクトを構成する全頂点を回転させているのである。図13に示される円周はより正確には、「Signboard2の底面の中心」のy軸周りの回転軌道であるが、オブジェクトの全頂点がそれぞれこういったy軸周りの回転軌道を回っているのである。
2D空間においても、1-6節や2-1節において類似の解説をしたが、3D空間においてオブジェクトを回転させる場合にも回転対象のオブジェクトが初期状態においてどのような位置、あるいは向きになっているのかという情報は重要である。それらの情報を元にして回転軸を決定することができるのである。
本節で述べたことから明らかであるが、一点だけ回転の方向について補足しておこう。
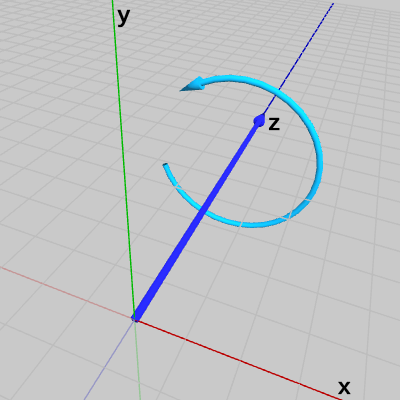
図3はz軸周りのプラス方向の回転(回転角度を増加させる回転)を示したものだが、図を見る限りでは このz軸周りの回転は反時計回りの回転である。ここで注意すべきことは、だからといってz軸周りの(プラス方向の)回転が常に反時計周りであるわけではないということである。回転の方向が時計回りであるか反時計周りであるかは、その回転を見る位置によって異なる。
例えば 図14は、球体が原点を中心とする半径$3$の円周上をz軸周りに回転している様子である (回転軸はz軸であり、この円周は$(3, 0, 0)$を通り、XY平面上にある)。球体の回転角度は毎フレーム 増加するように設定してある。
図から明らかなように、球体はこの円周上を反時計周りに回転しているが、それはz軸のマイナス側からこの回転を見ているためである。
実際、この回転をz軸プラス側から見たときの様子が図15であるが、この図を見れば回転が時計回りに行われていることが分かるだろう (z軸プラス側から見たときには、x軸プラス側は左側に位置し、z軸プラス側は奥ではなく手前に来る)。
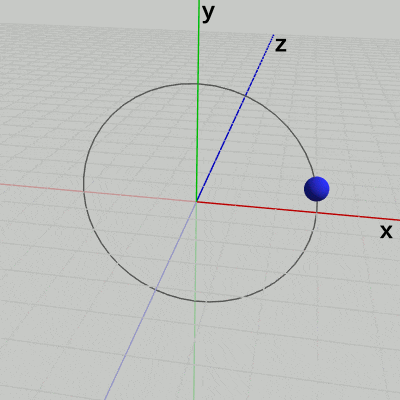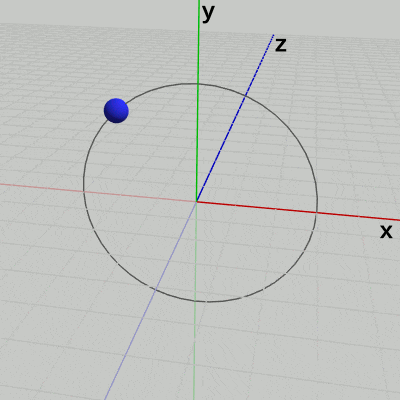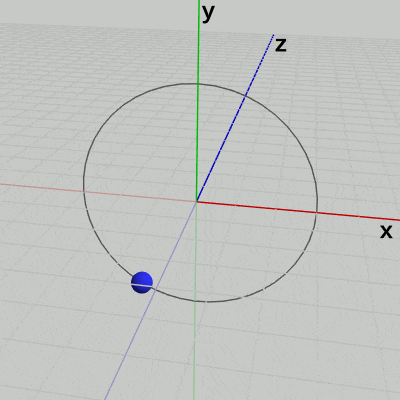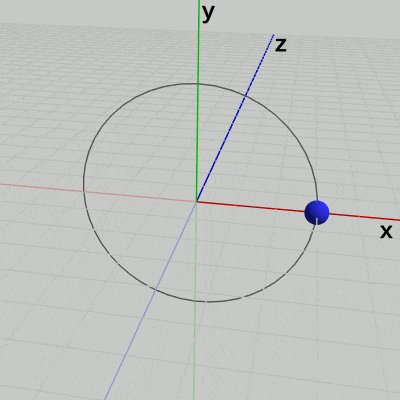
図14 z軸マイナス側から回転を見たときの様子 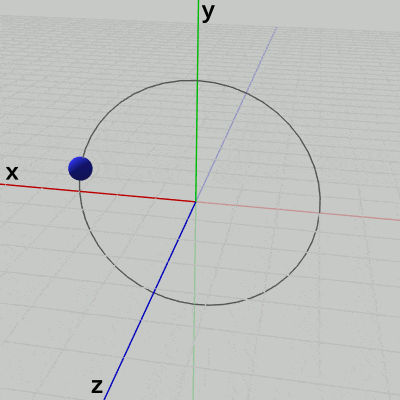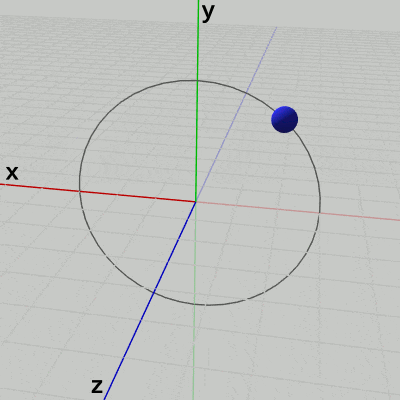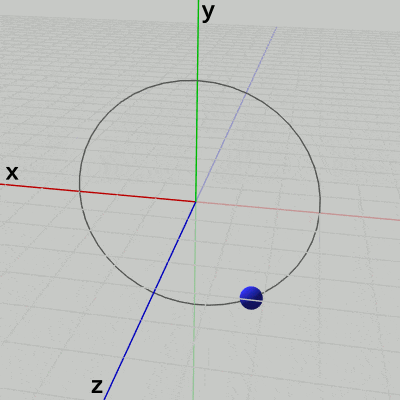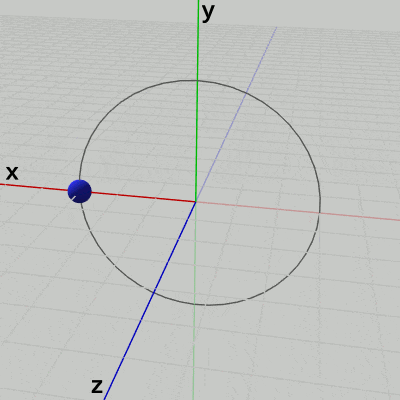
図15 z軸プラス側から回転を見たときの様子
回転の方向が時計回りであるか反時計周りであるかは、その回転を見る位置によって異なるが、回転の方向自体は上で述べたように左手系においては、左手の親指を回転軸とみなした場合、残りの指の曲がっている方向が回転のプラス方向である。「残りの指の曲がっている方向」についても、人差し指の側から曲がり方を見るのか、小指の側から曲がり方を見るかで、「曲がっている方向」が時計回りになったり反時計周りになったりするが、これは「回転を見る位置によって回転方向が異なる」ことを示す最も簡単な例である。
第1章、第2章で扱った2D空間は具体的にはXY平面であったが、図14を見れば2D空間におけるプラス方向の回転が反時計周りであった理由がわかるであろう。XY平面における回転は、具体的にはXY平面上にある2Dオブジェクトをz軸周りに回転させているのである (左手系における2D空間とは、XY平面をz軸のマイナス側から見ているのである)。
では、本節で扱った内容に関するプログラムを以下に示す。
[Code1] (実行結果 図16)
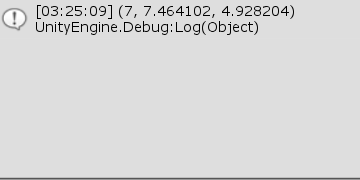
図16 Code1 実行結果 3行目の P1 が、点$P = (7, 8, -4)$をx軸周りに$60$°回転させた点であり、実行結果(図16)に示されるようにその位値は小数第2位までを四捨五入して表示すると $(7,\ 7.46,\ 4.93)$ である。
2行目の Vector3.right はVector3構造体の定数でありx軸プラス方向$(1, 0, 0)$を表している。
また、y軸、z軸についても同様の定数が用意されている。それぞれの値は以下のとおり。
Vector3.up : y軸プラス方向 $(0, 1, 0)$
Vector3.forward : z軸プラス方向 $(0, 0, 1)$
[Code2] (実行結果 図12、図13)
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図12、図13)。
また、同じ図17にある青いベクトルはXZ平面上に置かれており、z軸に平行である。Ball(の中心)から青いベクトルに垂線を下ろし、その足を点 $M$ とする (図18)。
ここでは、青いベクトルを回転軸としてBallを点 $M$ の周りに $90^\circ$ 回転させることについて考えてみよう (図19)。
上の解説で述べたように、行列(あるいはQuaternion)が表す3D空間の回転とは、原点を通る軸の周りの回転である。ここで回転軸としている青いベクトルは原点を通る軸ではない。青いベクトルは z軸に平行であるが、上図のBallに z軸周りの $90^\circ$ の回転を行っても、Ballは青いベクトルの周りに $90^\circ$ 回転するわけではない (図17の位置から z軸周りに $90^\circ$ 回転した位置に移動する)。
青いベクトルを回転軸とする回転は次のような手順で行えばよい。
図20は最初の状態であり、Ballの位置は $P$、回転中心の位置は $M$ である。
この状態から、Ball及び回転軸である青いベクトルを原点まで移動させる。具体的には、回転中心の位置が点 $M$ から原点に来るように移動させる (図21 ; 図21における回転中心の位置は原点)。
この移動によって青いベクトルは z軸に重なることになる (つまり、原点を通る軸になっている)。ここでBallを青いベクトルの周りに $90^\circ$ 回転させるが、青いベクトルは z軸に重なっているので、この回転は z軸周りの $90^\circ$ の回転と同じである (図21)。
最後に、Ball及び青いベクトルを元の位置まで戻せば、Ballは青いベクトルを回転軸として点 $M$ の周りを $90^\circ$ 回転した位置に移動している (図22)。
次のプログラムは今述べてきたことを実装したものである。
[Code3] (実行結果 図22)
今回の処理は初期化ブロックに記述されているので、プログラム実行後 1回だけ実行される。
Ballは開始時点ですでに回転前の位置 $P$ に置かれている。したがって、3行目の GetWorldPosition() によって wp にセットされる値は上図の $P$ の座標である。
5行目では wp - M を $90^\circ$ 回転させたときの位置を計算している (ここで使われている M は図中の $M$ の位置を表すVector3型の定数。ToVector4(..) は引数の値を同次座標化するカスタムライブラリーのメソッドで $w=1$ の4次元ベクトルが返される)。これは上で述べた、Ball及び青いベクトルを原点に移動させて $90^\circ$ 回転させる部分に相当する (回転中心が原点に来るように移動させるので移動量は -M である)。
6行目の pos += M は上記の、Ball及び青いベクトルを元の位置に戻す部分に相当する (元の位置に戻すには、回転中心が点 $M$ まで来ればよいので移動量は +M である)。
8行目の SetWorldPosition(pos) はカスタムライブラリーのメソッドであり、オブジェクトに対して引数で指定された分だけの平行移動を実行する。具体的には、前節で述べたオブジェクト原点を引数で指定された位置に移動させるものであり、行列による以下の処理と同じである。
本節では3D空間の回転行列のうちx軸、y軸、z軸といった基本的な軸周りの回転を扱う。
A) x軸、y軸、z軸を回転軸とする回転行列
以下の図はx軸、y軸、z軸を回転軸とした際のプラス方向の回転の様子を示したものである。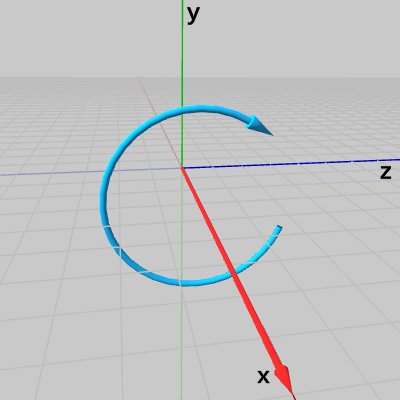 図1 x軸周りの回転
図1 x軸周りの回転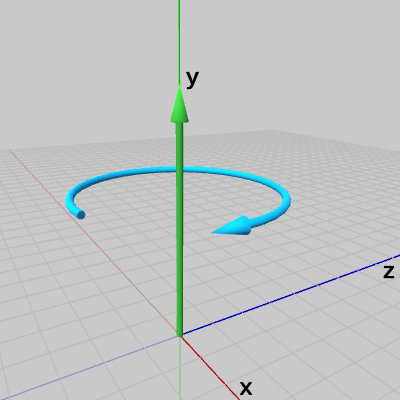 図2 y軸周りの回転
図2 y軸周りの回転 図3 z軸周りの回転
図3 z軸周りの回転

図1、図3が示すx軸、z軸周りの回転の場合でも、左手の親指を回転軸であるx軸、z軸に合わせれば残りの指の曲がっている方向は、図における水色の回転ベクトルの方向と一致する。
(注1 「回転のプラス方向」とは回転角度を増加させたときに進む方向である。回転角度を減少させれば反対の方向に進む)
3D空間における回転行列(Rotation Matrix)は $3\times3$行列で表すことができる。
x軸、y軸、z軸を回転軸として$\theta$だけ回転させる行列は以下のように表される(左からx軸周り、y軸周り、z軸周りの回転行列)。
\[\begin{pmatrix}1 &0 &0 \\0 &\cos\theta &-\sin\theta\\0 &\sin\theta &\cos\theta \end{pmatrix}\qquad\begin{pmatrix}\cos\theta &0 &\sin\theta\\0 &1 &0\\-\sin\theta &0 &\cos\theta\\\end{pmatrix}\qquad\begin{pmatrix}\cos\theta &-\sin\theta &0\\\sin\theta &\cos\theta &0\\0 &0 &1\end{pmatrix}\]
しかし実際には、3-7節でも述べたように3D空間における行列計算では同次座標に対応させるために、$3\times3$行列を1次元拡張した$4\times4$行列を使う。上の3つの回転行列を$4\times4$行列に拡張したものは以下のようになる。\[\begin{pmatrix}1 &0 &0 &0 \\0 &\cos\theta &-\sin\theta &0\\0 &\sin\theta &\cos\theta &0\\0 &0 &0 &1\end{pmatrix}\qquad\begin{pmatrix}\cos\theta &0 &\sin\theta &0\\0 &1 &0 &0\\-\sin\theta &0 &\cos\theta &0\\0 &0 &0 &1\end{pmatrix}\qquad\begin{pmatrix}\cos\theta &-\sin\theta &0 &0\\\sin\theta &\cos\theta &0 &0\\0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\]
B) 3D空間における回転
冒頭でも述べたが、3D空間における回転では角度の他に回転軸を指定する必要がある。そして、この回転軸は原点を通る軸(あるいは原点を始点とする軸)として考えなければならない。つまり、回転行列が表す回転は原点を通る軸周りの回転を表すのである(これはQuaternionでも同じである)。例えば、図5の点$P$を図に示される回転軸(淡い赤色のベクトル)の周りで回転させる場合について見ていこう。
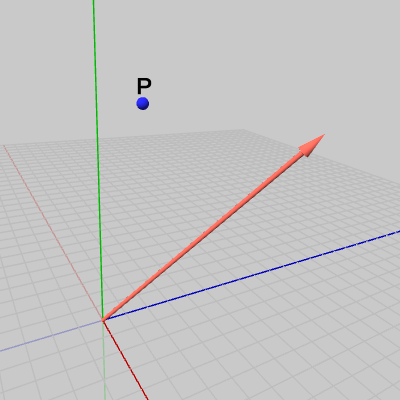 図5 点と回転軸
図5 点と回転軸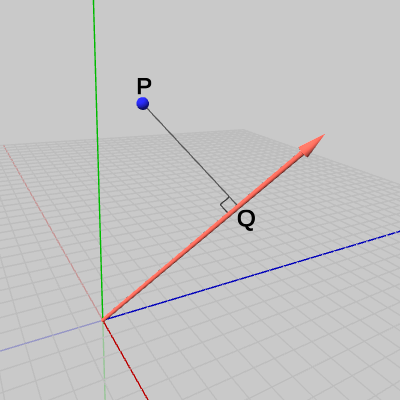 図6 点から回転軸へ垂線を下ろす
図6 点から回転軸へ垂線を下ろす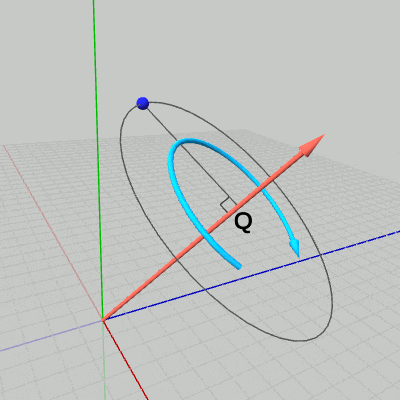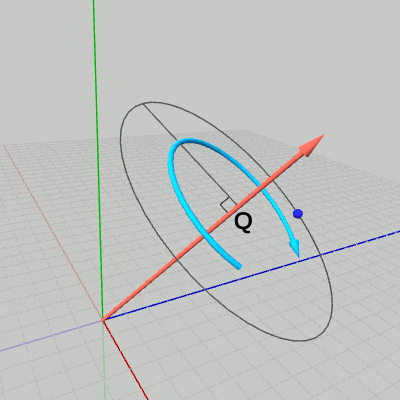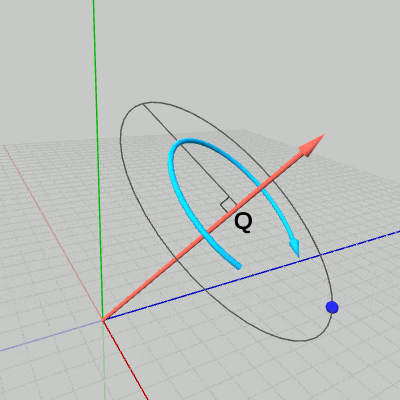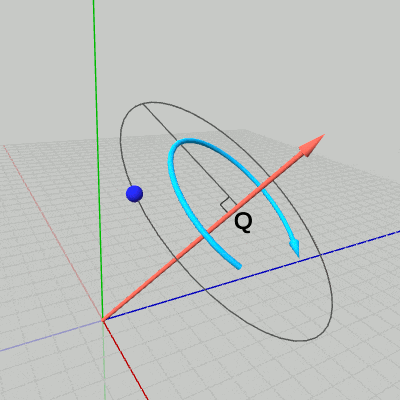 図7 回転軸周りの点の回転
図7 回転軸周りの点の回転
点$P$から回転軸へ垂線を下ろし、その足を点$Q$とする(図6 ; ある点から直線へ垂線を下ろすことについては3-4節参照)。このとき点$P$は、垂線の長さを半径とする点$Q$中心の円周上を回転することになる(図7)。回転軸は、図7の円周を含む平面の法線ベクトルになっている。
これが3D空間における回転である。
C) 点の回転
先ほどの回転行列の計算例として点$P = (a, b, c)$をx軸周りに$60$°だけ回転させる場合を以下に示す。\begin{align*}\begin{pmatrix}1 &0 &0 &0 \\0 &\cos{60^\circ} &-\sin{60^\circ} &0\\0 &\sin{60^\circ} &\cos{60^\circ} &0\\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}a \\b \\c \\1\end{pmatrix}&=\begin{pmatrix}1\cdot a + 0\cdot b + 0\cdot c + 0\cdot 1 \\0\cdot a + \cos{60^\circ}\cdot b -\sin{60^\circ}\cdot c + 0\cdot 1 \\0\cdot a + \sin{60^\circ}\cdot b + \cos{60^\circ}\cdot c + 0\cdot 1 \\0\cdot a + 0\cdot b + 0\cdot c + 1\cdot 1 \end{pmatrix}\\\\&=\begin{pmatrix}a \\b\cos{60^\circ} - c\sin{60^\circ} \\b\sin{60^\circ} + c\cos{60^\circ} \\1\end{pmatrix}\end{align*}


D) オブジェクトに回転行列を実行する
前節でも用いた以下の2つのオブジェクトに回転行列を実行する。両者とも初期状態での位置であり、図10のオブジェクトSignboard1はオブジェクトの底面の中心が原点に置かれており、図11のオブジェクトSignboard2は初期状態でのオブジェクトの底面の中心が$(2,\ 0,\ 1)$に置かれている。


(3D空間での)回転行列を取得するにあたっては、カスタムライブラリーの次のメソッドを使用する。
axisを回転軸として角度degだけ回転させる行列を取得する (戻り値は Matrix4x4型)。
TH3DMath.GetRotation4x4(float deg, Vector3 axis)
次のプログラムは、y軸を回転軸とする回転行列を取得し、オブジェクトに実行する処理である。回転角度を表すインスタンス変数i_degRotは毎フレーム$1$°ずつ増加するので、オブジェクトも毎フレーム$1$°ずつ回転する。
i_degRot++; Matrix4x4 R = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); Signboard#.SetMatrix(R); // # : 1 or 2
回転軸に指定されているVector3.upは、Unityに標準で用意されている定数で$(0, 1, 0)$、すなわちy軸のプラス方向を表す。


Signboard1は(初期状態において)オブジェクト自体に、回転軸であるy軸が貫通しているので、このプログラムを実行すると図12のような結果になる。Signboard2の場合は、初期状態の位置が回転軸であるy軸から離れた位置にあるため、y軸周りの回転では図13のような結果になる。Signboard2は初期状態では底面の中心が$(2, 0, 1)$に置かれていたが、そのために$(2, 0, 1)$からy軸へ下ろした垂線を半径とする円周上をSignboard2は回転することになる。
オブジェクトを回転させることは、より正確にいえばそのオブジェクトを構成する全頂点を回転させているのである。図13に示される円周はより正確には、「Signboard2の底面の中心」のy軸周りの回転軌道であるが、オブジェクトの全頂点がそれぞれこういったy軸周りの回転軌道を回っているのである。
2D空間においても、1-6節や2-1節において類似の解説をしたが、3D空間においてオブジェクトを回転させる場合にも回転対象のオブジェクトが初期状態においてどのような位置、あるいは向きになっているのかという情報は重要である。それらの情報を元にして回転軸を決定することができるのである。

図3 z軸周りの回転
図3はz軸周りのプラス方向の回転(回転角度を増加させる回転)を示したものだが、図を見る限りでは このz軸周りの回転は反時計回りの回転である。ここで注意すべきことは、だからといってz軸周りの(プラス方向の)回転が常に反時計周りであるわけではないということである。回転の方向が時計回りであるか反時計周りであるかは、その回転を見る位置によって異なる。
例えば 図14は、球体が原点を中心とする半径$3$の円周上をz軸周りに回転している様子である (回転軸はz軸であり、この円周は$(3, 0, 0)$を通り、XY平面上にある)。球体の回転角度は毎フレーム 増加するように設定してある。
図から明らかなように、球体はこの円周上を反時計周りに回転しているが、それはz軸のマイナス側からこの回転を見ているためである。
実際、この回転をz軸プラス側から見たときの様子が図15であるが、この図を見れば回転が時計回りに行われていることが分かるだろう (z軸プラス側から見たときには、x軸プラス側は左側に位置し、z軸プラス側は奥ではなく手前に来る)。


回転の方向が時計回りであるか反時計周りであるかは、その回転を見る位置によって異なるが、回転の方向自体は上で述べたように左手系においては、左手の親指を回転軸とみなした場合、残りの指の曲がっている方向が回転のプラス方向である。「残りの指の曲がっている方向」についても、人差し指の側から曲がり方を見るのか、小指の側から曲がり方を見るかで、「曲がっている方向」が時計回りになったり反時計周りになったりするが、これは「回転を見る位置によって回転方向が異なる」ことを示す最も簡単な例である。
第1章、第2章で扱った2D空間は具体的にはXY平面であったが、図14を見れば2D空間におけるプラス方向の回転が反時計周りであった理由がわかるであろう。XY平面における回転は、具体的にはXY平面上にある2Dオブジェクトをz軸周りに回転させているのである (左手系における2D空間とは、XY平面をz軸のマイナス側から見ているのである)。
では、本節で扱った内容に関するプログラムを以下に示す。
# Code1
まずは、3D空間上の点$P = (7, 8, -4)$をx軸周りに$60$°回転させる計算を行う。[Code1] (実行結果 図16)
Vector4 P = new Vector4(7.0f, 8.0f, -4.0f, 1.0f);
Matrix4x4 R = TH3DMath.GetRotation4x4(60.0f, Vector3.right);
Vector3 P1 = R * P;
Debug.Log("(" + P1.x + ", " + P1.y + ", " + P1.z + ")");

2行目の Vector3.right はVector3構造体の定数でありx軸プラス方向$(1, 0, 0)$を表している。
また、y軸、z軸についても同様の定数が用意されている。それぞれの値は以下のとおり。
Vector3.up : y軸プラス方向 $(0, 1, 0)$
Vector3.forward : z軸プラス方向 $(0, 0, 1)$
# Code2
次は上で扱った、Signboardを毎フレーム y軸周りに$1$°ずつ回転させるプログラムである。[Code2] (実行結果 図12、図13)
i_SB = 1;
i_degRot++;
Matrix4x4 R = TH3DMath.GetRotation4x4(i_degRot, Vector3.up);
if (i_SB == 1)
{
Signboard1.SetMatrix(R);
}
else
{
Signboard2.SetMatrix(R);
}
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図12、図13)。
# Code3
3D空間内の図17に示される位置に小さな球体オブジェクト Ball が置かれている。このときのBallの位置を $P$ とする (詳しくは、$P$ はBallの中心座標。Ballは球体オブジェクトであるが以下では点と捉えても構わない。Ballの初期状態における中心位置は原点である)。また、同じ図17にある青いベクトルはXZ平面上に置かれており、z軸に平行である。Ball(の中心)から青いベクトルに垂線を下ろし、その足を点 $M$ とする (図18)。
ここでは、青いベクトルを回転軸としてBallを点 $M$ の周りに $90^\circ$ 回転させることについて考えてみよう (図19)。
-
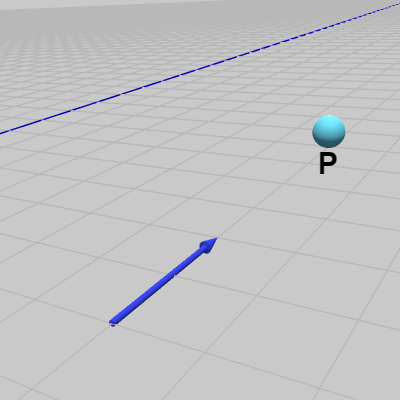 図17
図17 -
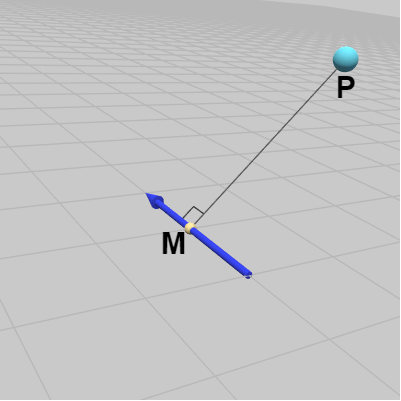 図18
図18 -
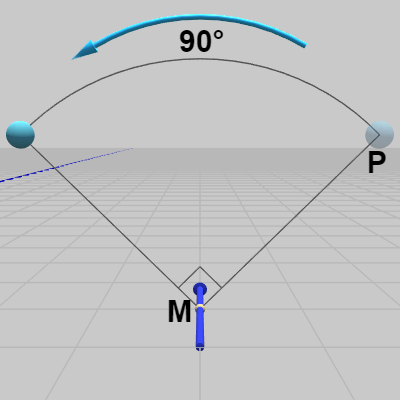 図19
図19
上の解説で述べたように、行列(あるいはQuaternion)が表す3D空間の回転とは、原点を通る軸の周りの回転である。ここで回転軸としている青いベクトルは原点を通る軸ではない。青いベクトルは z軸に平行であるが、上図のBallに z軸周りの $90^\circ$ の回転を行っても、Ballは青いベクトルの周りに $90^\circ$ 回転するわけではない (図17の位置から z軸周りに $90^\circ$ 回転した位置に移動する)。
青いベクトルを回転軸とする回転は次のような手順で行えばよい。
図20は最初の状態であり、Ballの位置は $P$、回転中心の位置は $M$ である。
この状態から、Ball及び回転軸である青いベクトルを原点まで移動させる。具体的には、回転中心の位置が点 $M$ から原点に来るように移動させる (図21 ; 図21における回転中心の位置は原点)。
この移動によって青いベクトルは z軸に重なることになる (つまり、原点を通る軸になっている)。ここでBallを青いベクトルの周りに $90^\circ$ 回転させるが、青いベクトルは z軸に重なっているので、この回転は z軸周りの $90^\circ$ の回転と同じである (図21)。
最後に、Ball及び青いベクトルを元の位置まで戻せば、Ballは青いベクトルを回転軸として点 $M$ の周りを $90^\circ$ 回転した位置に移動している (図22)。
-
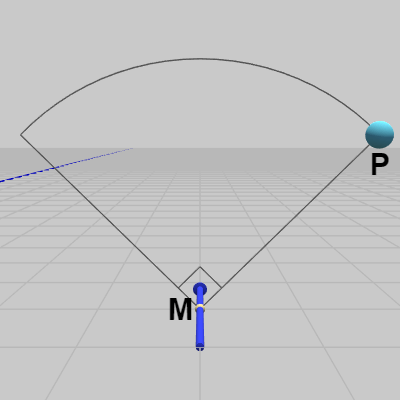 図20
図20 -
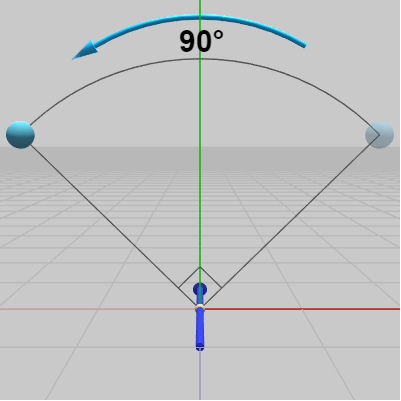 図21 回転中心の位置は原点 (青いベクトル周りの回転は、ここでは z軸周りの回転と同じ)
図21 回転中心の位置は原点 (青いベクトル周りの回転は、ここでは z軸周りの回転と同じ) -
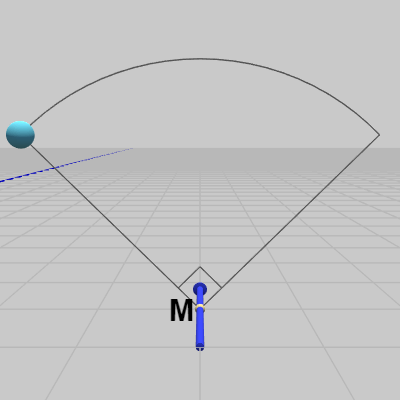 図22
図22
次のプログラムは今述べてきたことを実装したものである。
[Code3] (実行結果 図22)
if (!i_INITIALIZED)
{
Vector3 wp = Ball.GetWorldPosition();
Matrix4x4 R = TH3DMath.GetRotation4x4(90.0f, Vector3.forward);
Vector3 pos = R * TH3DMath.ToVector4(wp - M);
pos += M;
Ball.SetWorldPosition(pos);
i_INITIALIZED = true;
}
今回の処理は初期化ブロックに記述されているので、プログラム実行後 1回だけ実行される。
Ballは開始時点ですでに回転前の位置 $P$ に置かれている。したがって、3行目の GetWorldPosition() によって wp にセットされる値は上図の $P$ の座標である。
5行目では wp - M を $90^\circ$ 回転させたときの位置を計算している (ここで使われている M は図中の $M$ の位置を表すVector3型の定数。ToVector4(..) は引数の値を同次座標化するカスタムライブラリーのメソッドで $w=1$ の4次元ベクトルが返される)。これは上で述べた、Ball及び青いベクトルを原点に移動させて $90^\circ$ 回転させる部分に相当する (回転中心が原点に来るように移動させるので移動量は -M である)。
6行目の pos += M は上記の、Ball及び青いベクトルを元の位置に戻す部分に相当する (元の位置に戻すには、回転中心が点 $M$ まで来ればよいので移動量は +M である)。
8行目の SetWorldPosition(pos) はカスタムライブラリーのメソッドであり、オブジェクトに対して引数で指定された分だけの平行移動を実行する。具体的には、前節で述べたオブジェクト原点を引数で指定された位置に移動させるものであり、行列による以下の処理と同じである。
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos); Obj.SetMatrix(T);
© 2020-2025 Redpoll's 60 (All rights reserved)