Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-15
第3章 3D空間の基礎
$§$3-15 オイラー角 2
前節に引き続き、オイラー角による回転について扱う。本節ではオブジェクトの姿勢制御をオイラー角経由で行うことについて見ていく。本節前半は前節と同様に extrinsic rotations の Z-X-Yオーダーであるが、後半はオイラー角回転として一般的な形式である intrinsic rotations について扱う。
ここでは、姿勢を制御するための回転をオイラー角によって指定し、回転の表現形式には今まで通り回転行列を用いる。
問題を簡単にするために、今回はオブジェクトの姿勢制御に必要な回転行列は1つのみとし、この1つの回転行列をオブジェクトに実行することでオブジェクトの姿勢を制御する(例えば、人体のような複雑なオブジェクトの場合は、姿勢制御のために数十個から数百個のボーンと呼ばれるオブジェクトを用意し、人体を運動させる際には、それらのボーンの1つ1つに回転を実行するのである)。
図1のオブジェクトMiniPlaneは、初期状態で中心部分が原点に置かれており、オブジェクトの先端がちょうどz軸上の $z = -1$ にある。図2はMiniPlaneと半径1の球面である。球面の半径は$1$なので、初期状態でのMiniPlaneの先端は球面上の$(0,\ 0,\ -1)$にある。
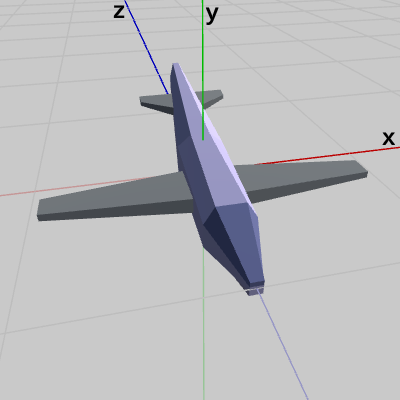
図1 MiniPlane 初期状態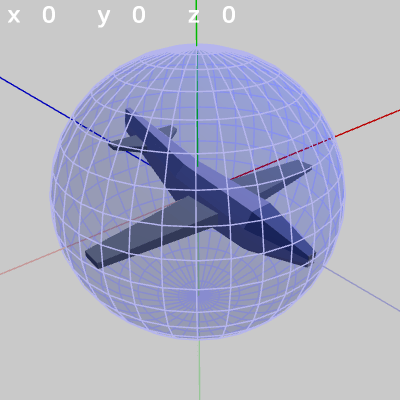 
図2 MiniPlaneと単位球面(半径1)
本節におけるアニメーションは、次のコードにおけるオイラー角の数値を変えてMiniPlaneに実行した結果である。
TH3DMath.GetEulerRotation4x4() は前節でも使用したカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。取得される回転行列 R_zxy は、z軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
i_eulX、i_eulY、i_eulZ は、それぞれ xｰ角度、y-角度、z-角度を表すインスタンス変数で、本節の図における白い数字はこれらの値を表したものである (前節と同じく本節においても x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度を x-角度、y-角度、z-角度 と表記する)。
以下の図は初期状態のMiniPlaneに対して、左から x-角度だけを変化させたもの、y-角度だけを変化させたもの、z-角度だけを変化させたものである。
前節と同様に球面上の縦方向の線を経線、横方向の線を緯線とすれば、これら３つの運動は次のように表される。
x-角度だけを変える場合、MiniPlaneの先端は縦方向の線、つまり経線上を動く(図3 ; 緯度の変化。y-角度を変化させていない状態ではx軸周りの回転と同じである)。
y-角度だけを変える場合、MiniPlaneの先端は横方向の線、つまり緯線上を動く(図4 ; 経度の変化)。
z-角度だけを変える場合は、MiniPlaneの先端は球面上での位置は変化しない。この場合のMiniPlaneは、その場所においてロール回転を行う（図5 ; ロール角度の変化。x-角度、y-角度を変化させていない状態におけるロール回転は図に示されるようにz軸周りの回転と同じである)。
次の図は、y-角度を左から $y = 60^\circ$、$y = -90^\circ$に固定して、x-角度だけを変化させたものである。
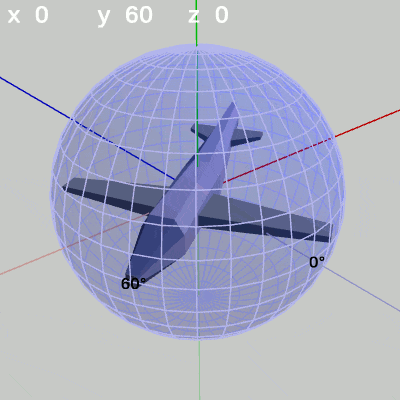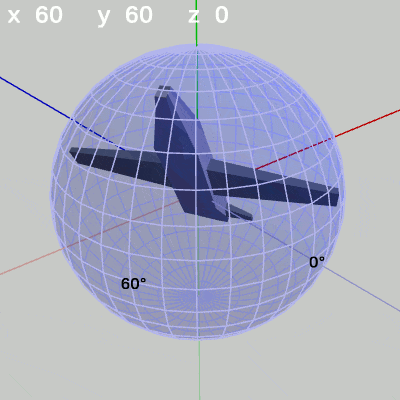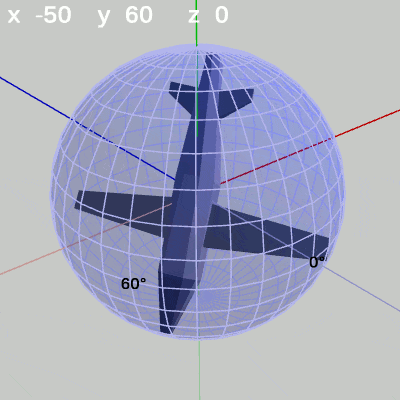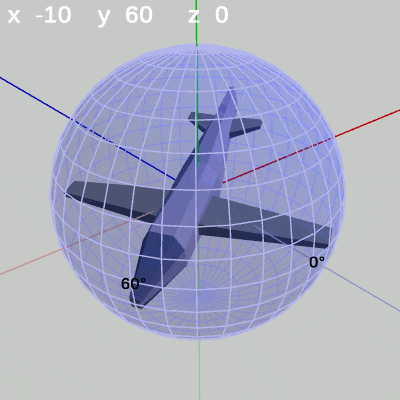
図6 x-角度の変化 (y = 60°)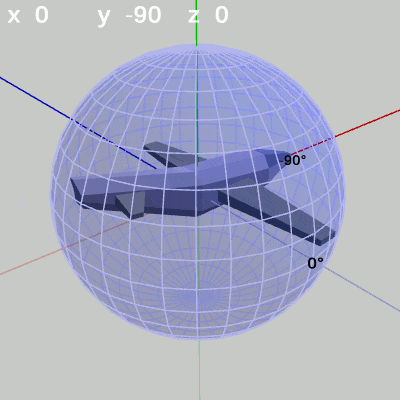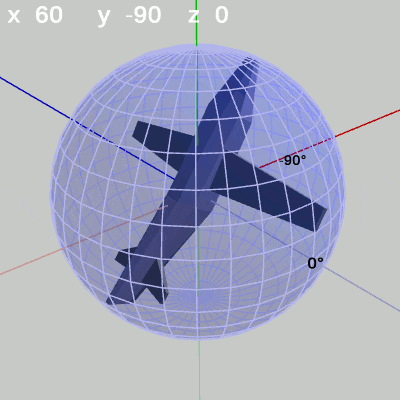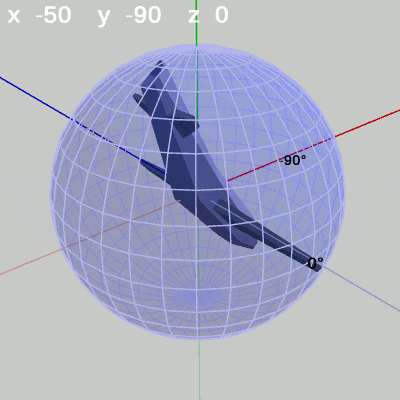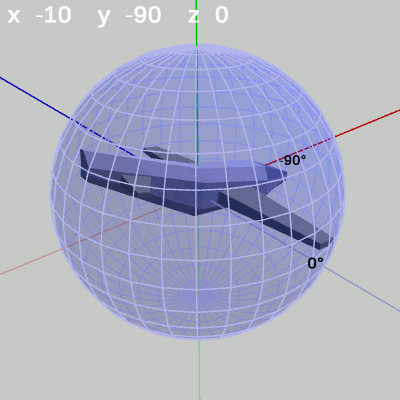 
図7 x-角度の変化 (y = -90°)
y-角度を $60^\circ$ に固定して、x-角度だけを変化させる場合は、MiniPlaneの先端が経度 $60^\circ$ の経線上を動く(図6)。
y-角度を $-90^\circ$ に固定して、x-角度だけを変化させる場合は、MiniPlaneの先端が経度 $-90^\circ$ の経線上を動く(図7)。
次の図は、x-角度、y-角度を左から $(x = 20^\circ,\ y = 80^\circ)$、$(x = -10^\circ,\ y = -120^\circ)$に固定して、z-角度だけを変化させたものである。
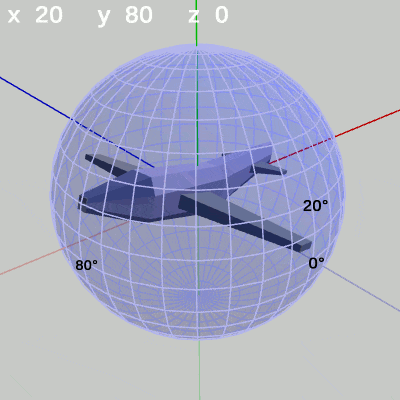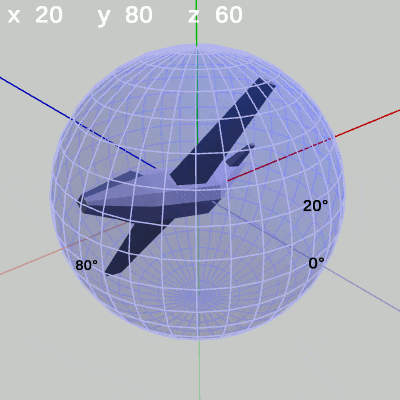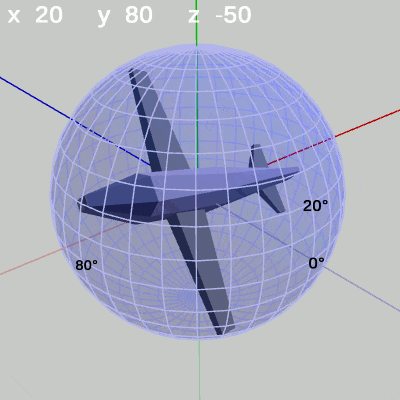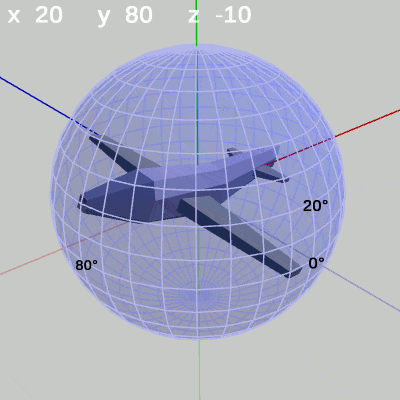
図8 z-角度の変化 (緯度 20°, 経度 80°) 
図9 z-角度の変化 (緯度 -10°, 経度 -120°)
z-角度だけを変化させる場合は、MiniPlaneの先端が球面上のどの位置にあっても、その場所でロール回転をするのである。たとえば、図8ではMiniPlaneの先端が球面上の緯度 $20^\circ$ 、経度 $80^\circ$ にある状態でロール回転をしている (図には表示されていないが、このロール回転はMiniPlaneの先端と原点を結ぶ軸を回転軸とする回転になっている)。
次の図は、x-角度を左から $x = 10^\circ$ 、$x = 20^\circ$ に固定して、y-角度だけを変化させたものである。
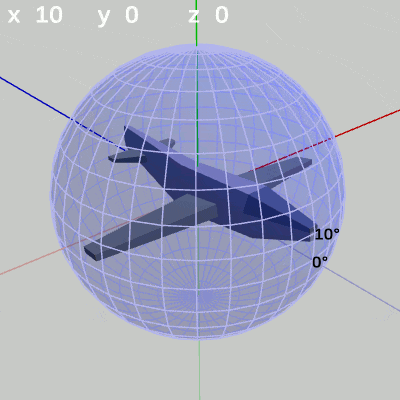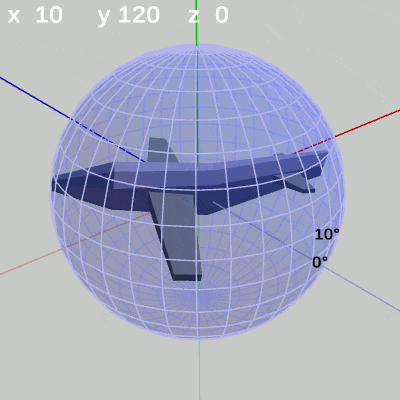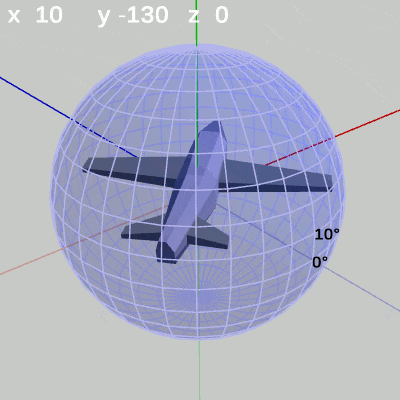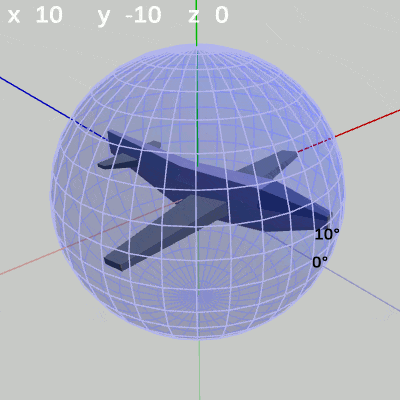
図10 y-角度の変化 (x = 10°)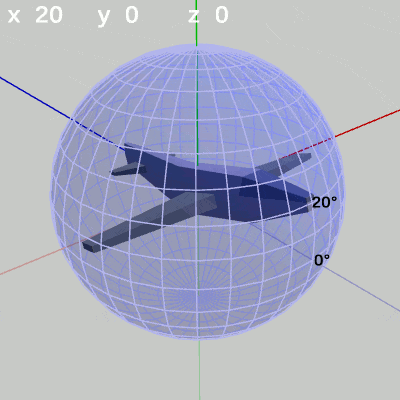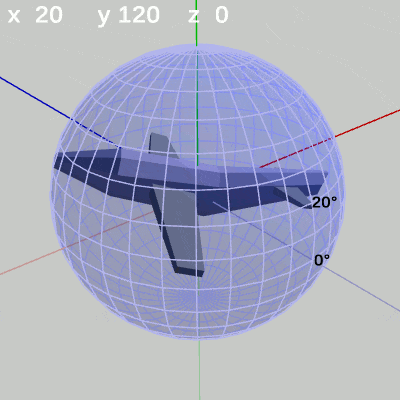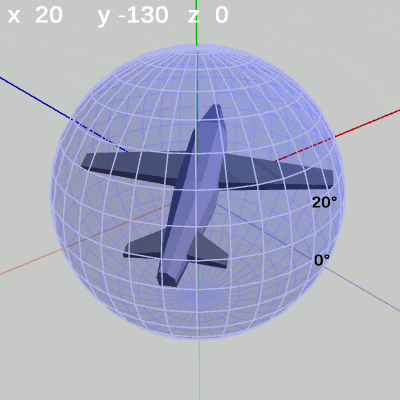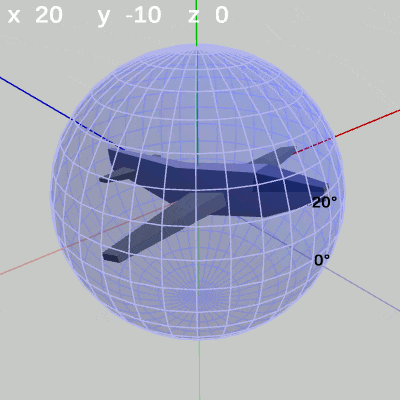 
図11 y-角度の変化 (x = 20°)
x-角度を $10^\circ$ に固定して、y-角度だけを変化させる場合は、MiniPlaneの先端が緯度 $10^\circ$ の緯線上を動く(図10)。
x-角度を $20^\circ$ に固定して、y-角度だけを変化させる場合は、MiniPlaneの先端が緯度 $20^\circ$ の緯線上を動く(図11)。
以上を要約する。
今回のMiniPlaneは初期状態で、その中心部分が原点に置かれている。このとき、MiniPlaneの先端はz軸上の $z = -1$ すなわち、$(0,\ 0, -1)$に位置している。オイラー角による回転行列をMiniPlaneに実行するとき、MiniPlaneの先端は半径$1$の球面上の運動を行うが、MiniPlaneの先端に着目してこの運動を述べると次のようになる。
Z-X-Yオーダーのオイラー角回転ではMiniPlaneの先端が、球面上のどこにあっても
x-角度を変化させると、その位置から縦方向、すなわち経線上を動く (緯度の変化)。
y-角度を変化させると、その位置から横方向、すなわち緯線上を動く(経度の変化。ただし極点においてはあてはまらない)。
z-角度を変化させると、その位置でロール回転を行う (ロール角度の変化)。
図12 y-角度の変化 (x = 70°)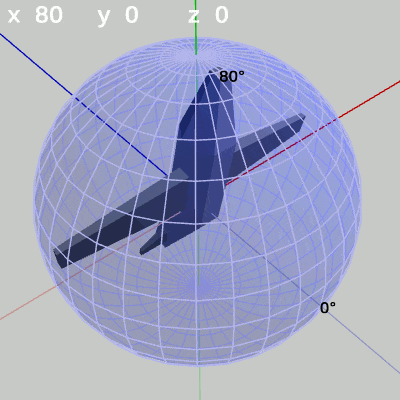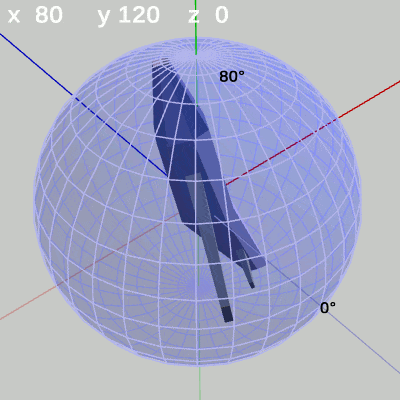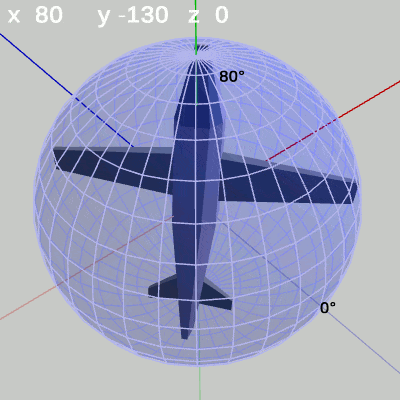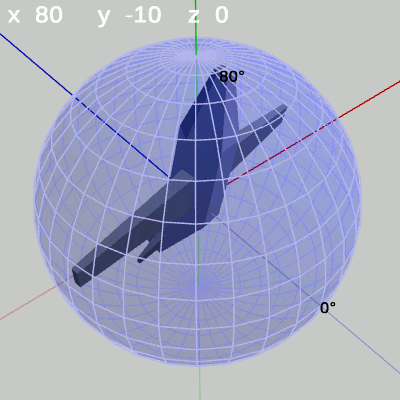 
図13 y-角度の変化 (x = 80°)
先ほどの図10、図11、及び今回の図12、図13はMiniPlaneの先端の緯線上の運動であるが、具体的には緯線の作る円周上をMiniPlaneの先端が回転することになる。図10、図11は緯度 $10^\circ$、緯度 $20^\circ$ の緯線上の運動であるが、そういった低緯度地帯では緯線の作る円周が大きいために、MiniPlaneの先端の動く範囲も大きい。
x-角度を増加させると、MiniPlaneはその先端をより高い緯度に向けるようになる。
図12、図13は緯度 $70^\circ$、緯度 $80^\circ$ の緯線上の運動であるが、このような高緯度地帯になると緯線の作る円周が小さくなるために、MiniPlaneの先端の動きも小さい範囲になっていく。
さらにx-角度を上げていき、最終的に $x = 90^\circ$ の状態にした結果が図14である。
図14においては、MiniPlaneの先端は球面上の極点(地球における北極)を向いている。極点には緯線が存在しないので、緯線の作る円周も存在しない。したがって、MiniPlaneの先端はこの状態においては緯線の作る円周上を動くということができなくなるわけである。
図14 x-角度 90°(x軸周りの90°の回転) 
図15 y-角度の変化 (x = 90° ; ジンバルロック)
オイラー角による回転において、このような状態をジンバルロック(Gimbal lock)という。図15は、この状態からy-角度を変化させたアニメーションである。
ジンバルロックでは運動の次元が1つ減るといった表現もされる。今回の例では、y-角度を変化させてもMiniPlaneの先端は(緯線がないために)緯線方向の運動ができなくなっている。
では、図14の状態から x-角度を変化させたもの、z-角度を変化させたものを図16、図17に示す。
図16 x-角度の変化 (x = 90° を中心とする)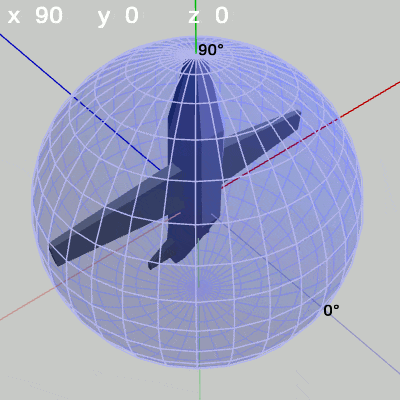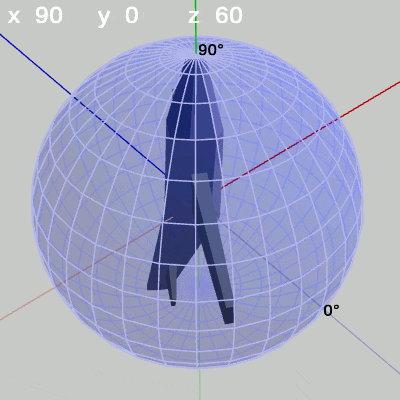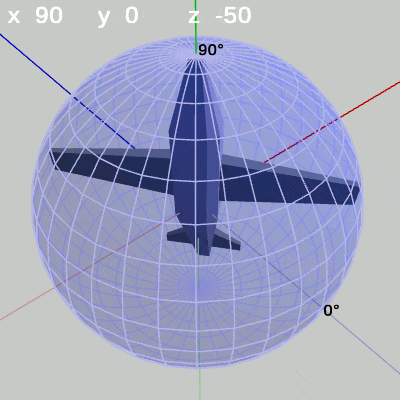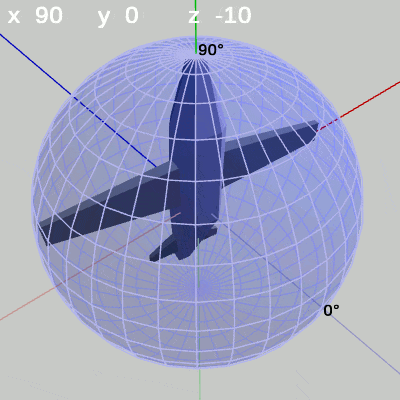 
図17 z-角度の変化 (x = 90°)
MiniPlaneの先端が極点を向いている場合でも、x-角度を変化させれば先端部分は経線上を動く(図16)。
z-角度を変化させると、その位置でロール回転をすると先に述べたが、この場合のようにMiniPlaneの先端が極点を向いている場合でも z-角度を変化させると、他の場合と変わりなくロール回転をする(図17)。
図15、図17を比較すればわかるように、Z-X-Yオーダーのジンバルロックでは y-角度を変化させる運動と、z-角度を変化させる運動は同じものになってしまうのである (すなわちジンバルロックにおいては経度の変化とロール角度の変化の区別がつかない)。
以下、重要な点について一つ注意しておく。ここまでにおいてオイラー角の3つの角度が緯度、経度、ロール角度としての役割を持つことを見てきたが、これは必ずしも自明なことではない。3つの角度が緯度、経度、ロール角度として'現れる'のはオブジェクトの初期状態を適切に定めた場合においてである。オブジェクトの初期状態を適切に定めなければこういったことは見えてこない。
例えば上の例ではMiniPlaneは初期状態(x-角度、y-角度、z-角度が $0^\circ$ の状態)において z軸マイナス方向を向くように置かれていた。このように初期状態を定めることで x-角度、y-角度、z-角度が緯度、経度、ロール角度として現れたが、これは細かく言えば(extrinsic rotationsの) Z-X-Yオーダーの場合である。Z-X-Yオーダーの場合にはオブジェクトの初期状態の向きを z軸方向に定めれば、x-角度、y-角度、z-角度が緯度、経度、ロール角度としての役割を持つのである。
下図18はMiniPlaneの初期状態の向きを(z軸マイナス方向ではなく) z軸プラス方向としたものであり、右図19はこのMiniPlaneの x-角度、y-角度、z-角度をそれぞれ $-30^\circ$、$70^\circ$、$40^\circ$ としたときの状態であるが、図に示されるようにMiniPlaneは 緯度 $30^\circ$、経度 $70^\circ$ の位置において $40^\circ$ のロール回転をした状態になっている。すなわちこの場合にも x-角度、y-角度、z-角度が緯度、経度、ロール角度としての役割になっているわけである (正確には下の例では x-角度の符号を反転したものが緯度に一致する。また下の例で使用している球面の起点は z軸マイナス側ではなく z軸プラス側に置かれている)。
図18 初期状態において z軸プラス方向を向いている (x-角度、y-角度、z-角度はいずれも 0°) 
図19 x-角度 -30°、y-角度 70°、z-角度 40°
もし Z-X-Yオーダーの場合にオブジェクトの初期状態の向きを z軸方向に定めない場合はどうなるかを見てみよう。下図20は初期状態のMiniPlaneの向きを x軸プラス方向としたものである。右図21はこのMiniPlaneの x-角度、y-角度、z-角度を適当に変化させているときの様子であるが、このアニメーションに見られるようにこの場合には x-角度や z-角度の変化は緯度やロール角度の変化にはなっていない (もちろん緯度やロール角度としての役割も持たない。y-角度の変化はこの場合でも経度の変化に相当する)。
そしてこの場合には x-角度、y-角度、z-角度の数値からオブジェクトがどのような状態にあるのかを読み解くのは困難であり、それぞれの角度を変化させてオブジェクトがどのような状態になるかを予測するのも困難である。
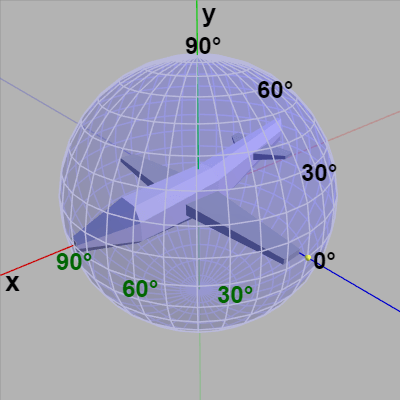
図20 初期状態の向き x軸プラス方向 (x-角度、y-角度、z-角度はいずれも 0°)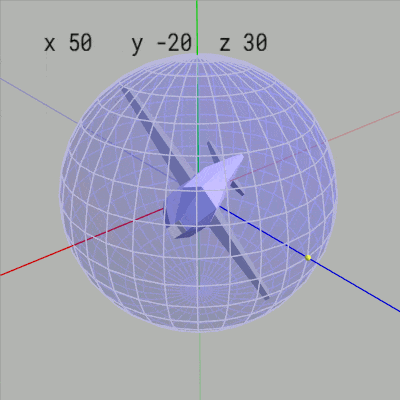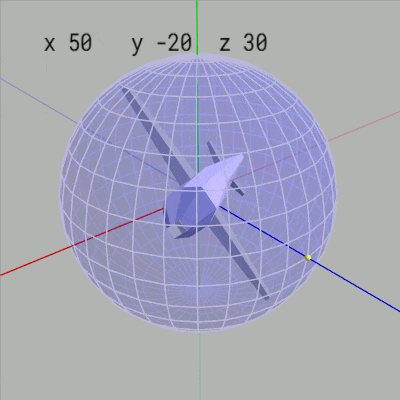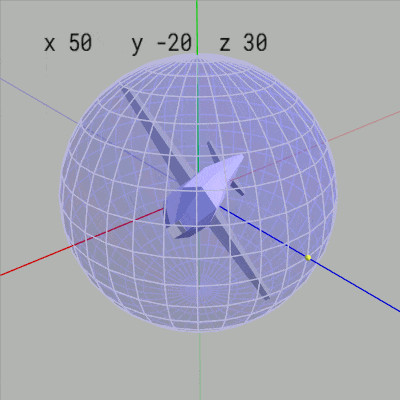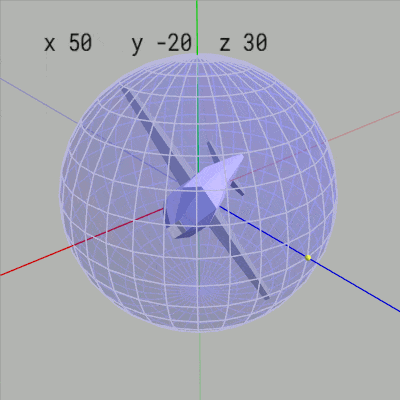 
図21 この場合には x-角度、z-角度は緯度やロール角度としての役割は持たない
再述するがオイラー角で使われる3つの角度が緯度、経度、ロール角度として現れるのはオブジェクトの初期状態を適切に定めた場合においてである。もし上の例のようにオブジェクトの初期状態を適切に定めていない場合には緯度、経度、ロール角度としての役割は見えてこないのである。
今までの extrinsic rotations 形式のオイラー角回転では座標系は固定されており、その固定された座標系の軸周りに回転を行うものであった (これを親座標系の軸周りの回転という)。これに対し intrinsic rotations ではオブジェクトのローカル座標系と呼ばれる座標系の軸周りに回転を行う。そしてこのローカル座標系の軸周りの回転において重要なのは、回転時にオブジェクトと座標系が一体となって回転するという点である。
下左図は extrinsic rotations の X-Y-Zオーダーで x-角度 $40^\circ$、y-角度 $-30^\circ$、z-角度 $70^\circ$ の順で回転する様子である。下右図は intrinsic rotations の Z-Y-Xオーダーで z-角度 $70^\circ$、y-角度 $-30^\circ$、x-角度 $40^\circ$ の順で回転する様子である。右図に示されるように intrinsic rotations の場合はオブジェクトに設定されているローカル座標系の軸周りの回転となっており、オブジェクトとローカル座標系が一体となって回転を行っている。
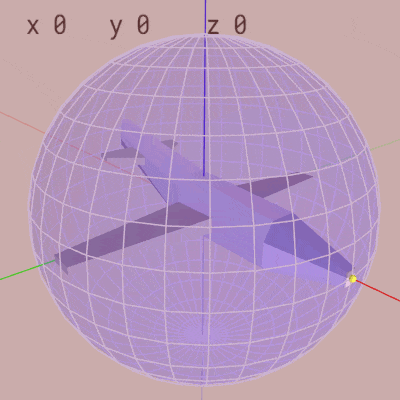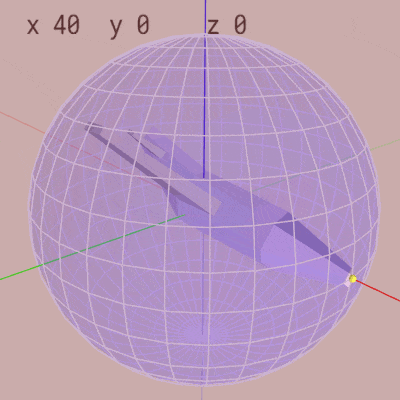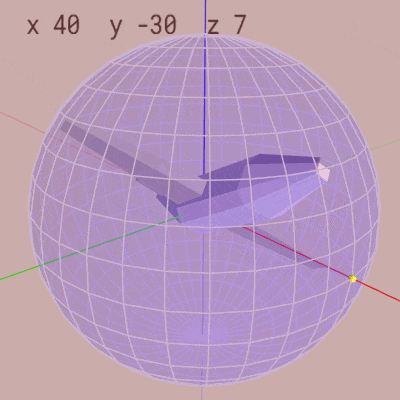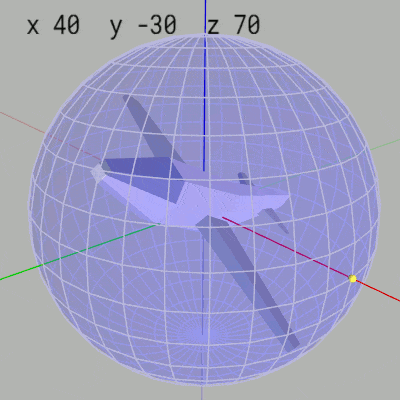
図22 extrinsic rotations : X-Y-Z 
図23 intrinsic rotations : Z-Y-X
そして上の2つのアニメーションでは回転後のオブジェクトの状態が同じ状態になっている。具体的には extrinsic rotations でも intrinsic rotations でも回転後においては、MiniPlaneが緯度 $30^\circ$、経度 $70^\circ$ を向いた状態で $40^\circ$ のロール回転をした状態になっている。
これは extrinsic rotations と intrinsic rotations が逆順の関係にあるためにこのような一致が起こるのである。例えば extrinsic rotations で x軸周りに $\alpha$、y軸周りに $\beta$、z軸周りに $\gamma$ の順で回転を行った結果と、intrinsic rotations で z軸周りに $\gamma$、y軸周りに $\beta$、x軸周りに $\alpha$ の順で回転を行ったときの結果は一致するのである (extrinsic rotations と intrinsic rotations が逆順の関係にあるのは親座標系の軸周りの回転とローカル座標系の軸周りの回転が逆順の関係にあるためである。この点については6-3節で解説する)。
そしてこのことからも分かるように intrinsic rotations においてもオイラー角回転に使われる3つの角度はそれぞれ球面上における緯度、経度、ロール角度としての役割を持っている。以下、代表的な2つのケースで intrinsic rotations について見ていこう (今までと同様以下の解説においても使われる座標系は左手系である)。
$\mathbf{(\mathrm{i})}$ Z-Y-X
ローカル座標系の z軸、y軸、x軸の順で回転を行うものである。intrinsic rotations の Z-Y-Xオーダーでは z-角度が経度、y-角度が緯度、x-角度がロール角度としての役割を持つ (この例では y-角度の符号を反転したものが球面上の緯度に一致する)。ただし上でも注意したようにオブジェクトの初期状態を適切に定めなければこういったことは見えてこない。
Z-Y-Xオーダーの場合は下図24に示されるようにオブジェクトが x軸プラス方向を向いた状態を初期状態として定める。そして使用する球面もその起点が +x軸上に、北極点が +z軸上に、南極点が -z軸上に位置するように置く。このように定めることで下右図に示されるように z-角度を変化させると経度が変化し、y-角度を変化させると緯度が変化し、x-角度を変化させるとロール角度が変化する。
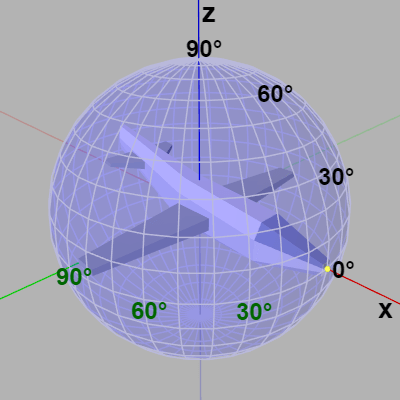
図24 Z-Y-Xオーダーにおける初期状態 (x-角度、y-角度、z-角度はいずれも 0°) 
図25 z-角度が経度、y-角度(の符号を反転したもの)が緯度、x-角度がロール角度に相当する
それぞれの軸周りの回転行列を $R_x$、$R_y$、$R_z$ とすると intrinsic rotations の Z-Y-Xオーダーはこれら3つの回転行列の積として以下のように表される。
\[ R_{zyx} = R_z R_y R_x \]3-8節で述べたように列優先の場合には行列の積は右から左に掛けていくのであった。しかし上記の積では一番最初の回転である z軸周りの回転($R_z$)が積の一番左に来ている。これもまたローカル座標系の軸周りの回転であることに由来するものである。
先程 extrinsic rotations と intrinsic rotations は逆順の関係にあると述べたが、それらを表す回転行列の積もまた逆順の関係になる。つまり extrinsic rotations の場合は通常通り行列の積は右から左に掛けるが、intrinsic rotations の場合には行列の積を左から右に掛けていくのである。
そのために intrinsic rotations の Z-Y-Xオーダーでは z軸周りの回転行列 $R_z$、y軸周りの回転行列 $R_y$、x軸周りの回転行列 $R_x$ が上記のように左から $R_z$、$R_y$、$R_x$ の順で掛けられるのである (この点についても6-3節で解説する)。
したがってプログラムにすると以下のようになる (i_eulX、i_eulY、i_eulZ は各軸周りの回転角度を表すインスタンス変数であるが、これらを $10^\circ$ ずつ変化させたときの実行結果が上図25である)。
Z-Y-Xオーダーでは y-角度の変化は緯度の変化につながる。例えば x-角度 $60^\circ$、y-角度 $-40^\circ$、z-角度 $50^\circ$ はMiniPlane先端が緯度 $40^\circ$、経度 $60^\circ$ の位置に置かれ、$50^\circ$ のロール回転をした状態であるが、ここから y-角度を $10^\circ$ ずつ増加させるとMiniPlane先端が緯度 $40^\circ$ の位置から $10^\circ$ ずつ下に下がっていく (図26)。
なぜ y-角度の変化が緯度の変化になるかについては右図27を見れば明らかであろう。
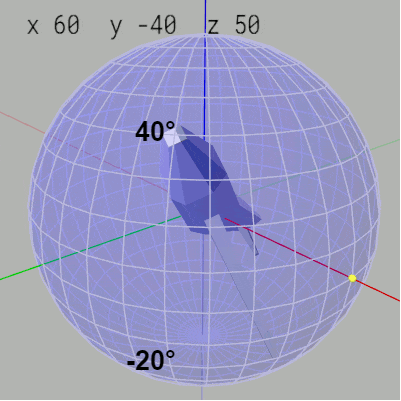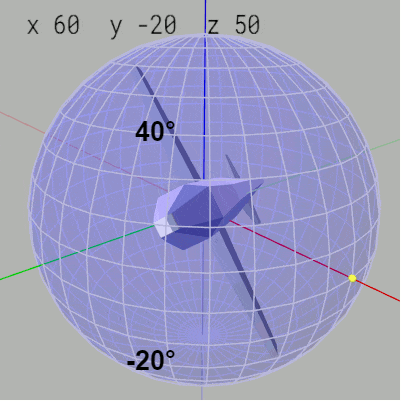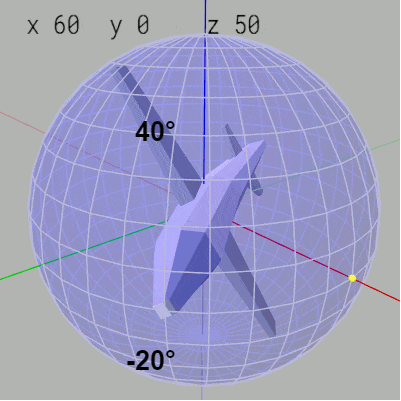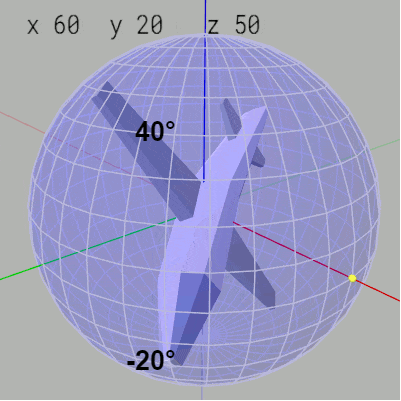
図26 y-角度を10°ずつ増加させるとMiniPlane先端の緯度が10°ずつ下に下がる 
図27 赤いフィルターのかかった状態はオイラー角回転の実行過程 (通常色のフレームをつないで表示したものが左図のアニメーション)
図27のアニメーションにおいて赤いフィルターのかかった状態はオイラー角回転(z軸、y軸、x軸の順で回転)が行われている過程であり、通常色の状態はそのオイラー角回転の実行結果である。通常色のフレームをつないで表示したものが左図のアニメーションである。図27のアニメーションに示されるように第2の回転である y軸周りの回転角度が $10^\circ$ ずつ増加するが、これによってMiniPlane先端が置かれる緯度が $10^\circ$ ずつ下に下がっていく結果になる。
$\mathbf{(\mathrm{ii})}$ Z-Y-Z
ローカル座標系の z軸、y軸、z軸の順で回転を行うものである。便宜上以下の解説では最初の z軸周りの回転角度を「z1-角度」、2回目の z軸周りの回転角度を「z2-角度」と表記する。intrinsic rotations の Z-Y-Zオーダーでは z1-角度が経度、y-角度が緯度、z2-角度がロール角度としての役割を持つが、正確には以下の例では y-角度を $\theta$ とするとき $90^\circ-\theta$ が球面上の緯度に一致する。
Z-Y-Zオーダーの場合は下図28に示されるようにオブジェクトが z軸プラス方向を向いた状態を初期状態として定める (使用する球面は先程のZ-Y-Xのものと同じで起点が +x軸上、北極点が +z軸上)。このように定めることで下右図に示されるように z1-角度を変化させると経度が変化し、y-角度を変化させると緯度が変化し、z2-角度を変化させるとロール角度が変化する。
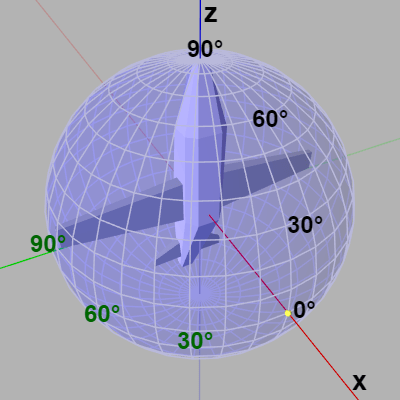
図28 Z-Y-Zオーダーにおける初期状態 (z1-角度、y-角度、z2-角度はいずれも 0°) 
図29 z1-角度が経度、y-角度が緯度、z2‐角度がロール角度に相当する (正確には y-角度を θ としたとき、90‐θ が緯度に一致する)
それぞれの軸周りの回転行列を $R_{z1}$、$R_y$、$R_{z2}$ とすると intrinsic rotations の Z-Y-Zオーダーはこれら3つの回転行列の積として以下のように表される。
\[ R_{zyz} = R_{z1} R_y R_{z2} \]
プログラムにすると以下のように記述される (i_eulZ1、i_eulY、i_eulZ2 は各軸周りの回転角度を表すインスタンス変数であるが、これらを $10^\circ$ ずつ変化させたときの実行結果が上図29である)。
Z-Y-Zオーダーでは z1-角度の変化は経度の変化につながる。例えば z1-角度 $80^\circ$、y-角度 $70^\circ$、z2-角度 $30^\circ$ はMiniPlane先端が緯度 $20^\circ\ (=90^\circ - 70^\circ)$、経度 $80^\circ$ の位置に置かれ、$30^\circ$ のロール回転をした状態であるが、ここから z1-角度を $10^\circ$ ずつ減少させるとMiniPlane先端が経度 $80^\circ$ の位置から $10^\circ$ ずつ右に移動する (図30)。
図30では z1-角度は $80^\circ$ から $20^\circ$ まで減少するが、図31はそれぞれの状態におけるオイラー角回転の実行過程である。
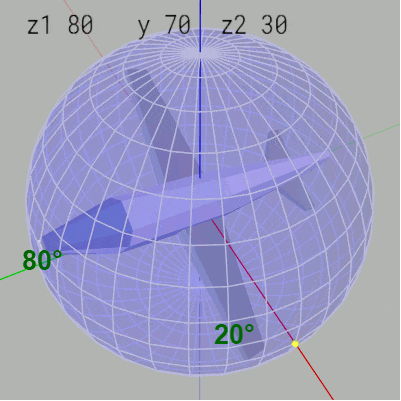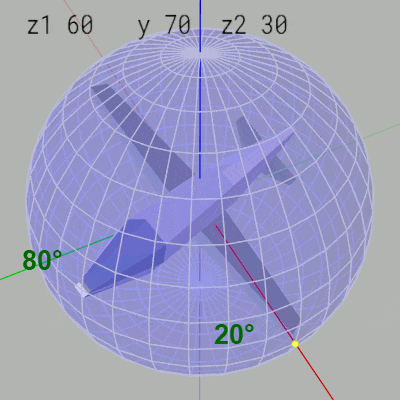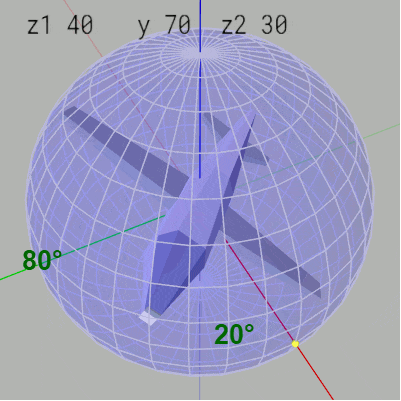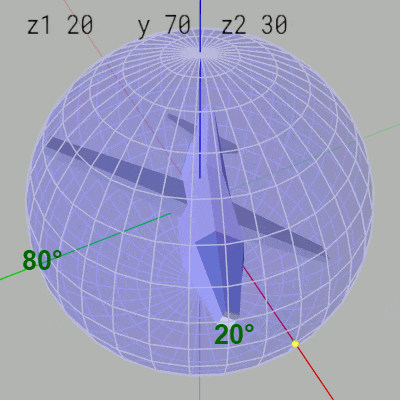
図30 z1-角度を10°ずつ減少させるとMiniPlane先端の経度が10°ずつ減少する(右に移動する) 
図31 赤いフィルターのかかった状態はオイラー角回転の実行過程 (通常色のフレームをつないで表示したものが左図のアニメーション)
z1-角度が $10^\circ$ ずつ減少することは、最初の z軸周りの回転角度が $10^\circ$ ずつ減少することを意味するが、それによってMiniPlane先端の置かれる経度が $10^\circ$ ずつ減少する結果となる。
図28に示されるように Z-Y-Zオーダーでは初期状態がジンバルロックの状態から始まる (3つの軸を使用するオイラー角回転ではジンバルロックは緯度を表す角度が $90^\circ$ あるいは $-90^\circ$ のときに起こるが、2つの軸によるオイラー角回転のジンバルロックは緯度を表す角度が $0^\circ$ あるいは $180^\circ$ のときに起こる)。
上で述べたようにジンバルロックの状態では経度の変化とロール角度の変化の区別がつかない。今回は初期状態で z軸プラス方向を向いた状態になっているため、(ローカル座標系の) z軸周りの回転はロール回転になる。しかしジンバルロックの状態では z軸周りの回転をロール角度の変化ではなく経度の変化として扱うことができる。これによって2つの軸しか用いていないにもかかわらず3つの軸を用いた場合と同様の回転を実現できるのである (つまり2つの軸によるオイラー角回転はジンバルロックを利用しているわけである)。
[Code1]
このプログラムは、Xキー、Yキー、Zキーを押して i_eulX、i_eulY、i_eulZ の値を変化させるもので、1回押すごとに角度が $10^\circ$ ずつ増加する(長押しには対応していない)。また、Shiftキーと同時に押すと角度が $10^\circ$ ずつ減少する (プログラム中の THUtil.IsShiftDown() はShiftキーが押されていればtrueを返すカスタムライブラリのメソッドである)。
なお、このCode1及び次のCode2では x-角度の変更範囲は $-90^\circ$ から $90^\circ$ の範囲に制限してある。つまり、x-角度を押し続けても $90^\circ$ あるいは $-90^\circ$ を越える値にはならない。
プログラム実行中に各キーを押すことで、MiniPlaneの先端が球面上において経線、緯線上を $10^\circ$ ずつ移動したり、あるいは MiniPlaneがそのときいる場所において $10^\circ$ ずつロール回転を行うようになる。
[Code2]
このプログラムは、Code1において Input.GetKeyDown(..) となっていた箇所を Input.GetKey(..) に変え、1フレームあたりの角度の増減を $1^\circ$ ずつに変更しただけである。
上記と同様に X キー、Y キー、Z キーを押すことでそれぞれの角度が $10^\circ$ ずつ変化する。
[Code3] (実行結果 図25)
使用するキーは今までと同じであるが、X キーが z1-角度に、Z キーが z2-角度に対応している。
[Code4] (実行結果 図29)
A) オブジェクトの姿勢制御
オブジェクトに対して実行する変換は平行移動、回転、スケールの3つである。3D空間内におけるオブジェクトの運動は、この3つの変換を合成したものをオブジェクトに対して実行することで実現される。オブジェクトの姿勢制御は、オブジェクトに対して実行する3つの変換のうち、主として回転に関係するものである。すなわち、オブジェクトに何らかの姿勢をとらせるためには、その姿勢にするために必要な回転をオブジェクトに実行する必要がある。ここでは、姿勢を制御するための回転をオイラー角によって指定し、回転の表現形式には今まで通り回転行列を用いる。
問題を簡単にするために、今回はオブジェクトの姿勢制御に必要な回転行列は1つのみとし、この1つの回転行列をオブジェクトに実行することでオブジェクトの姿勢を制御する(例えば、人体のような複雑なオブジェクトの場合は、姿勢制御のために数十個から数百個のボーンと呼ばれるオブジェクトを用意し、人体を運動させる際には、それらのボーンの1つ1つに回転を実行するのである)。
図1のオブジェクトMiniPlaneは、初期状態で中心部分が原点に置かれており、オブジェクトの先端がちょうどz軸上の $z = -1$ にある。図2はMiniPlaneと半径1の球面である。球面の半径は$1$なので、初期状態でのMiniPlaneの先端は球面上の$(0,\ 0,\ -1)$にある。
本節におけるアニメーションは、次のコードにおけるオイラー角の数値を変えてMiniPlaneに実行した結果である。
Matrix4x4 R_zxy = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ); MiniPlane.SetMatrix(R_zxy);
TH3DMath.GetEulerRotation4x4() は前節でも使用したカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。取得される回転行列 R_zxy は、z軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
i_eulX、i_eulY、i_eulZ は、それぞれ xｰ角度、y-角度、z-角度を表すインスタンス変数で、本節の図における白い数字はこれらの値を表したものである (前節と同じく本節においても x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度を x-角度、y-角度、z-角度 と表記する)。
以下の図は初期状態のMiniPlaneに対して、左から x-角度だけを変化させたもの、y-角度だけを変化させたもの、z-角度だけを変化させたものである。
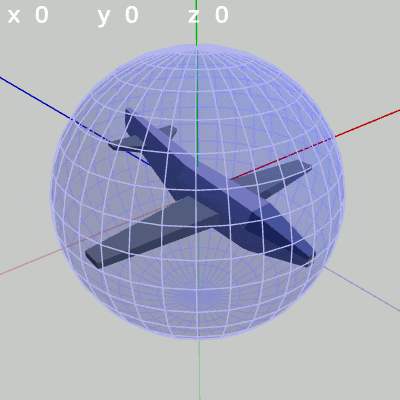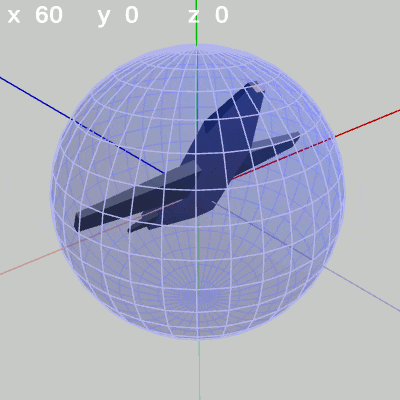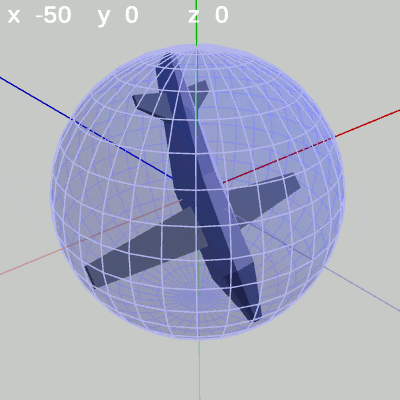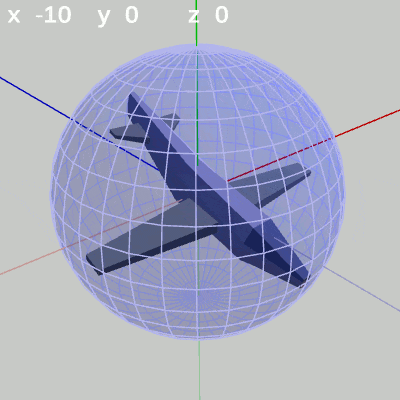図3 x-角度を変化させる
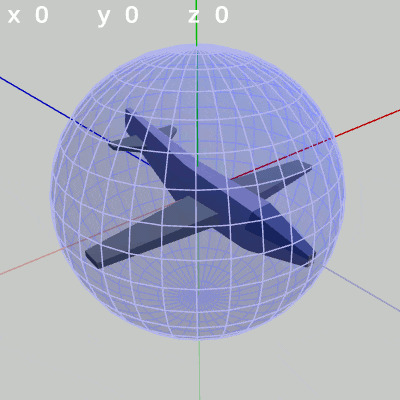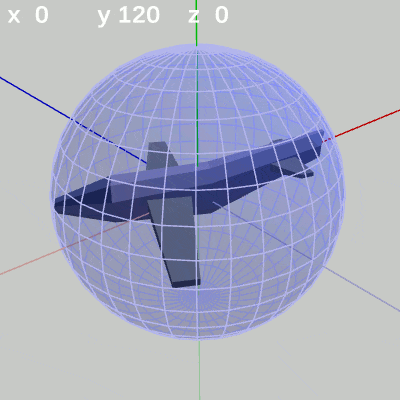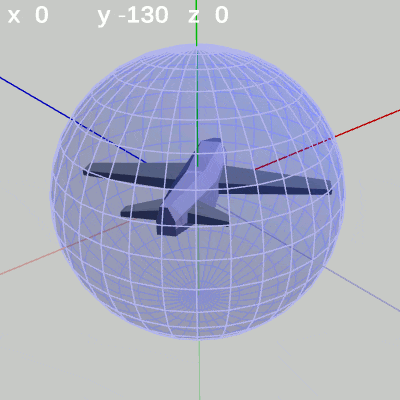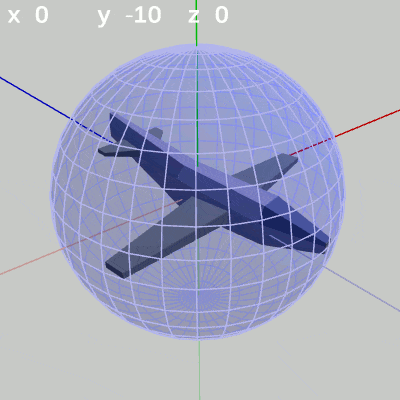図4 y-角度を変化させる
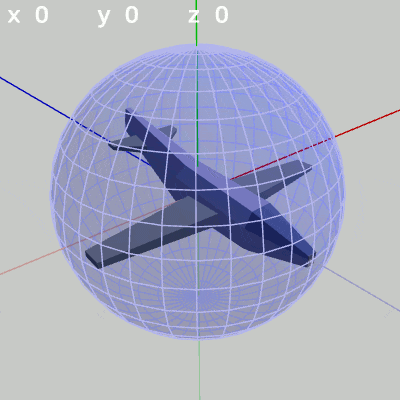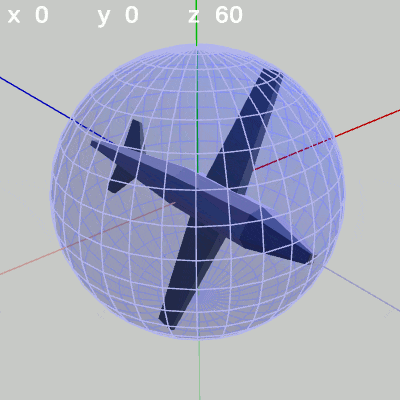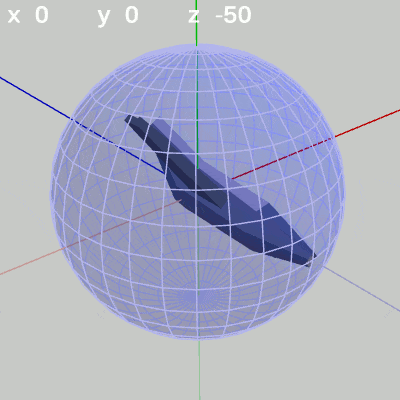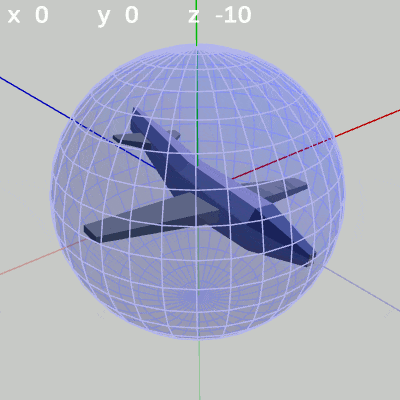図5 z-角度を変化させる (ロール回転)
前節と同様に球面上の縦方向の線を経線、横方向の線を緯線とすれば、これら３つの運動は次のように表される。
x-角度だけを変える場合、MiniPlaneの先端は縦方向の線、つまり経線上を動く(図3 ; 緯度の変化。y-角度を変化させていない状態ではx軸周りの回転と同じである)。
y-角度だけを変える場合、MiniPlaneの先端は横方向の線、つまり緯線上を動く(図4 ; 経度の変化)。
z-角度だけを変える場合は、MiniPlaneの先端は球面上での位置は変化しない。この場合のMiniPlaneは、その場所においてロール回転を行う（図5 ; ロール角度の変化。x-角度、y-角度を変化させていない状態におけるロール回転は図に示されるようにz軸周りの回転と同じである)。
次の図は、y-角度を左から $y = 60^\circ$、$y = -90^\circ$に固定して、x-角度だけを変化させたものである。
y-角度を $60^\circ$ に固定して、x-角度だけを変化させる場合は、MiniPlaneの先端が経度 $60^\circ$ の経線上を動く(図6)。
y-角度を $-90^\circ$ に固定して、x-角度だけを変化させる場合は、MiniPlaneの先端が経度 $-90^\circ$ の経線上を動く(図7)。
次の図は、x-角度、y-角度を左から $(x = 20^\circ,\ y = 80^\circ)$、$(x = -10^\circ,\ y = -120^\circ)$に固定して、z-角度だけを変化させたものである。
z-角度だけを変化させる場合は、MiniPlaneの先端が球面上のどの位置にあっても、その場所でロール回転をするのである。たとえば、図8ではMiniPlaneの先端が球面上の緯度 $20^\circ$ 、経度 $80^\circ$ にある状態でロール回転をしている (図には表示されていないが、このロール回転はMiniPlaneの先端と原点を結ぶ軸を回転軸とする回転になっている)。
次の図は、x-角度を左から $x = 10^\circ$ 、$x = 20^\circ$ に固定して、y-角度だけを変化させたものである。
x-角度を $10^\circ$ に固定して、y-角度だけを変化させる場合は、MiniPlaneの先端が緯度 $10^\circ$ の緯線上を動く(図10)。
x-角度を $20^\circ$ に固定して、y-角度だけを変化させる場合は、MiniPlaneの先端が緯度 $20^\circ$ の緯線上を動く(図11)。
以上を要約する。
今回のMiniPlaneは初期状態で、その中心部分が原点に置かれている。このとき、MiniPlaneの先端はz軸上の $z = -1$ すなわち、$(0,\ 0, -1)$に位置している。オイラー角による回転行列をMiniPlaneに実行するとき、MiniPlaneの先端は半径$1$の球面上の運動を行うが、MiniPlaneの先端に着目してこの運動を述べると次のようになる。
Z-X-Yオーダーのオイラー角回転ではMiniPlaneの先端が、球面上のどこにあっても
x-角度を変化させると、その位置から縦方向、すなわち経線上を動く (緯度の変化)。
y-角度を変化させると、その位置から横方向、すなわち緯線上を動く(経度の変化。ただし極点においてはあてはまらない)。
z-角度を変化させると、その位置でロール回転を行う (ロール角度の変化)。
B) ジンバルロック
次の図12、図13は、x-角度を左から $x = 70^\circ$ 、$x = 80^\circ$ に固定して、y-角度だけを変化させたものである。それぞれ、MiniPlaneの先端が緯度 $70^\circ$、$80^\circ$ の緯線上で運動することになる。 先ほどの図10、図11、及び今回の図12、図13はMiniPlaneの先端の緯線上の運動であるが、具体的には緯線の作る円周上をMiniPlaneの先端が回転することになる。図10、図11は緯度 $10^\circ$、緯度 $20^\circ$ の緯線上の運動であるが、そういった低緯度地帯では緯線の作る円周が大きいために、MiniPlaneの先端の動く範囲も大きい。
x-角度を増加させると、MiniPlaneはその先端をより高い緯度に向けるようになる。
図12、図13は緯度 $70^\circ$、緯度 $80^\circ$ の緯線上の運動であるが、このような高緯度地帯になると緯線の作る円周が小さくなるために、MiniPlaneの先端の動きも小さい範囲になっていく。
さらにx-角度を上げていき、最終的に $x = 90^\circ$ の状態にした結果が図14である。
図14においては、MiniPlaneの先端は球面上の極点(地球における北極)を向いている。極点には緯線が存在しないので、緯線の作る円周も存在しない。したがって、MiniPlaneの先端はこの状態においては緯線の作る円周上を動くということができなくなるわけである。
オイラー角による回転において、このような状態をジンバルロック(Gimbal lock)という。図15は、この状態からy-角度を変化させたアニメーションである。
ジンバルロックでは運動の次元が1つ減るといった表現もされる。今回の例では、y-角度を変化させてもMiniPlaneの先端は(緯線がないために)緯線方向の運動ができなくなっている。
では、図14の状態から x-角度を変化させたもの、z-角度を変化させたものを図16、図17に示す。
MiniPlaneの先端が極点を向いている場合でも、x-角度を変化させれば先端部分は経線上を動く(図16)。
z-角度を変化させると、その位置でロール回転をすると先に述べたが、この場合のようにMiniPlaneの先端が極点を向いている場合でも z-角度を変化させると、他の場合と変わりなくロール回転をする(図17)。
図15、図17を比較すればわかるように、Z-X-Yオーダーのジンバルロックでは y-角度を変化させる運動と、z-角度を変化させる運動は同じものになってしまうのである (すなわちジンバルロックにおいては経度の変化とロール角度の変化の区別がつかない)。
以下、重要な点について一つ注意しておく。ここまでにおいてオイラー角の3つの角度が緯度、経度、ロール角度としての役割を持つことを見てきたが、これは必ずしも自明なことではない。3つの角度が緯度、経度、ロール角度として'現れる'のはオブジェクトの初期状態を適切に定めた場合においてである。オブジェクトの初期状態を適切に定めなければこういったことは見えてこない。
例えば上の例ではMiniPlaneは初期状態(x-角度、y-角度、z-角度が $0^\circ$ の状態)において z軸マイナス方向を向くように置かれていた。このように初期状態を定めることで x-角度、y-角度、z-角度が緯度、経度、ロール角度として現れたが、これは細かく言えば(extrinsic rotationsの) Z-X-Yオーダーの場合である。Z-X-Yオーダーの場合にはオブジェクトの初期状態の向きを z軸方向に定めれば、x-角度、y-角度、z-角度が緯度、経度、ロール角度としての役割を持つのである。
下図18はMiniPlaneの初期状態の向きを(z軸マイナス方向ではなく) z軸プラス方向としたものであり、右図19はこのMiniPlaneの x-角度、y-角度、z-角度をそれぞれ $-30^\circ$、$70^\circ$、$40^\circ$ としたときの状態であるが、図に示されるようにMiniPlaneは 緯度 $30^\circ$、経度 $70^\circ$ の位置において $40^\circ$ のロール回転をした状態になっている。すなわちこの場合にも x-角度、y-角度、z-角度が緯度、経度、ロール角度としての役割になっているわけである (正確には下の例では x-角度の符号を反転したものが緯度に一致する。また下の例で使用している球面の起点は z軸マイナス側ではなく z軸プラス側に置かれている)。
もし Z-X-Yオーダーの場合にオブジェクトの初期状態の向きを z軸方向に定めない場合はどうなるかを見てみよう。下図20は初期状態のMiniPlaneの向きを x軸プラス方向としたものである。右図21はこのMiniPlaneの x-角度、y-角度、z-角度を適当に変化させているときの様子であるが、このアニメーションに見られるようにこの場合には x-角度や z-角度の変化は緯度やロール角度の変化にはなっていない (もちろん緯度やロール角度としての役割も持たない。y-角度の変化はこの場合でも経度の変化に相当する)。
そしてこの場合には x-角度、y-角度、z-角度の数値からオブジェクトがどのような状態にあるのかを読み解くのは困難であり、それぞれの角度を変化させてオブジェクトがどのような状態になるかを予測するのも困難である。
再述するがオイラー角で使われる3つの角度が緯度、経度、ロール角度として現れるのはオブジェクトの初期状態を適切に定めた場合においてである。もし上の例のようにオブジェクトの初期状態を適切に定めていない場合には緯度、経度、ロール角度としての役割は見えてこないのである。
C) intrinsic rotations
ここからはオイラー角のもう1つの形式である intrinsic rotations について解説する。一般にはオイラー角といえば intrinsic rotations のことであり、例えば物理などでオイラー角が言及される際に使われるのは intrinsic rotations である。今までの extrinsic rotations 形式のオイラー角回転では座標系は固定されており、その固定された座標系の軸周りに回転を行うものであった (これを親座標系の軸周りの回転という)。これに対し intrinsic rotations ではオブジェクトのローカル座標系と呼ばれる座標系の軸周りに回転を行う。そしてこのローカル座標系の軸周りの回転において重要なのは、回転時にオブジェクトと座標系が一体となって回転するという点である。
下左図は extrinsic rotations の X-Y-Zオーダーで x-角度 $40^\circ$、y-角度 $-30^\circ$、z-角度 $70^\circ$ の順で回転する様子である。下右図は intrinsic rotations の Z-Y-Xオーダーで z-角度 $70^\circ$、y-角度 $-30^\circ$、x-角度 $40^\circ$ の順で回転する様子である。右図に示されるように intrinsic rotations の場合はオブジェクトに設定されているローカル座標系の軸周りの回転となっており、オブジェクトとローカル座標系が一体となって回転を行っている。
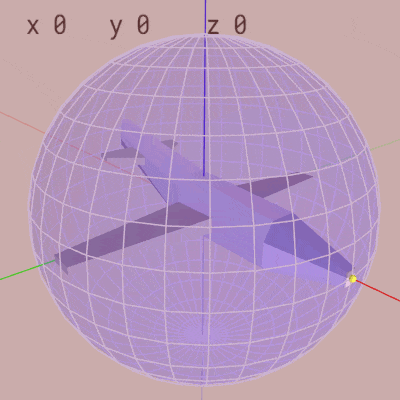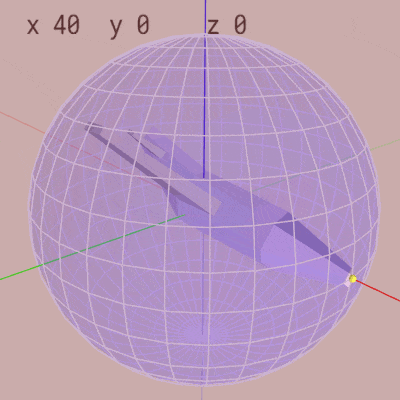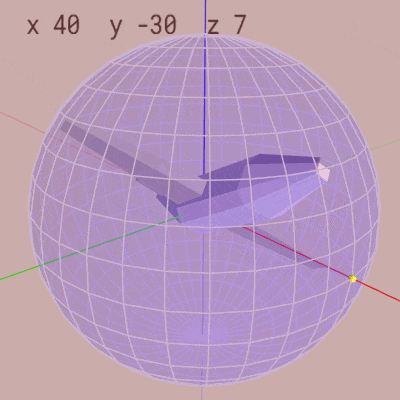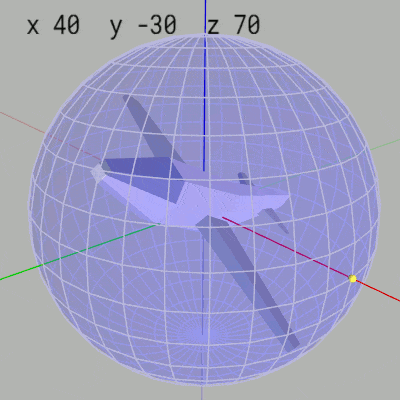
そして上の2つのアニメーションでは回転後のオブジェクトの状態が同じ状態になっている。具体的には extrinsic rotations でも intrinsic rotations でも回転後においては、MiniPlaneが緯度 $30^\circ$、経度 $70^\circ$ を向いた状態で $40^\circ$ のロール回転をした状態になっている。
これは extrinsic rotations と intrinsic rotations が逆順の関係にあるためにこのような一致が起こるのである。例えば extrinsic rotations で x軸周りに $\alpha$、y軸周りに $\beta$、z軸周りに $\gamma$ の順で回転を行った結果と、intrinsic rotations で z軸周りに $\gamma$、y軸周りに $\beta$、x軸周りに $\alpha$ の順で回転を行ったときの結果は一致するのである (extrinsic rotations と intrinsic rotations が逆順の関係にあるのは親座標系の軸周りの回転とローカル座標系の軸周りの回転が逆順の関係にあるためである。この点については6-3節で解説する)。
そしてこのことからも分かるように intrinsic rotations においてもオイラー角回転に使われる3つの角度はそれぞれ球面上における緯度、経度、ロール角度としての役割を持っている。以下、代表的な2つのケースで intrinsic rotations について見ていこう (今までと同様以下の解説においても使われる座標系は左手系である)。
$\mathbf{(\mathrm{i})}$ Z-Y-X
ローカル座標系の z軸、y軸、x軸の順で回転を行うものである。intrinsic rotations の Z-Y-Xオーダーでは z-角度が経度、y-角度が緯度、x-角度がロール角度としての役割を持つ (この例では y-角度の符号を反転したものが球面上の緯度に一致する)。ただし上でも注意したようにオブジェクトの初期状態を適切に定めなければこういったことは見えてこない。
Z-Y-Xオーダーの場合は下図24に示されるようにオブジェクトが x軸プラス方向を向いた状態を初期状態として定める。そして使用する球面もその起点が +x軸上に、北極点が +z軸上に、南極点が -z軸上に位置するように置く。このように定めることで下右図に示されるように z-角度を変化させると経度が変化し、y-角度を変化させると緯度が変化し、x-角度を変化させるとロール角度が変化する。
それぞれの軸周りの回転行列を $R_x$、$R_y$、$R_z$ とすると intrinsic rotations の Z-Y-Xオーダーはこれら3つの回転行列の積として以下のように表される。
\[ R_{zyx} = R_z R_y R_x \]3-8節で述べたように列優先の場合には行列の積は右から左に掛けていくのであった。しかし上記の積では一番最初の回転である z軸周りの回転($R_z$)が積の一番左に来ている。これもまたローカル座標系の軸周りの回転であることに由来するものである。
先程 extrinsic rotations と intrinsic rotations は逆順の関係にあると述べたが、それらを表す回転行列の積もまた逆順の関係になる。つまり extrinsic rotations の場合は通常通り行列の積は右から左に掛けるが、intrinsic rotations の場合には行列の積を左から右に掛けていくのである。
そのために intrinsic rotations の Z-Y-Xオーダーでは z軸周りの回転行列 $R_z$、y軸周りの回転行列 $R_y$、x軸周りの回転行列 $R_x$ が上記のように左から $R_z$、$R_y$、$R_x$ の順で掛けられるのである (この点についても6-3節で解説する)。
したがってプログラムにすると以下のようになる (i_eulX、i_eulY、i_eulZ は各軸周りの回転角度を表すインスタンス変数であるが、これらを $10^\circ$ ずつ変化させたときの実行結果が上図25である)。
// intrinsic rotations (Z-Y-X) Matrix4x4 Rx = TH3DMath.GetRotation4x4(i_eulX, Vecotr3.right); Matrix4x4 Ry = TH3DMath.GetRotation4x4(i_eulY, Vecotr3.up); Matrix4x4 Rz = TH3DMath.GetRotation4x4(i_eulZ, Vecotr3.forward); Matrix4x4 Rzyx = Rz * Ry * Rx; MiniPlane.SetMatrix(Rzyx);
Z-Y-Xオーダーでは y-角度の変化は緯度の変化につながる。例えば x-角度 $60^\circ$、y-角度 $-40^\circ$、z-角度 $50^\circ$ はMiniPlane先端が緯度 $40^\circ$、経度 $60^\circ$ の位置に置かれ、$50^\circ$ のロール回転をした状態であるが、ここから y-角度を $10^\circ$ ずつ増加させるとMiniPlane先端が緯度 $40^\circ$ の位置から $10^\circ$ ずつ下に下がっていく (図26)。
なぜ y-角度の変化が緯度の変化になるかについては右図27を見れば明らかであろう。
図27のアニメーションにおいて赤いフィルターのかかった状態はオイラー角回転(z軸、y軸、x軸の順で回転)が行われている過程であり、通常色の状態はそのオイラー角回転の実行結果である。通常色のフレームをつないで表示したものが左図のアニメーションである。図27のアニメーションに示されるように第2の回転である y軸周りの回転角度が $10^\circ$ ずつ増加するが、これによってMiniPlane先端が置かれる緯度が $10^\circ$ ずつ下に下がっていく結果になる。
$\mathbf{(\mathrm{ii})}$ Z-Y-Z
ローカル座標系の z軸、y軸、z軸の順で回転を行うものである。便宜上以下の解説では最初の z軸周りの回転角度を「z1-角度」、2回目の z軸周りの回転角度を「z2-角度」と表記する。intrinsic rotations の Z-Y-Zオーダーでは z1-角度が経度、y-角度が緯度、z2-角度がロール角度としての役割を持つが、正確には以下の例では y-角度を $\theta$ とするとき $90^\circ-\theta$ が球面上の緯度に一致する。
Z-Y-Zオーダーの場合は下図28に示されるようにオブジェクトが z軸プラス方向を向いた状態を初期状態として定める (使用する球面は先程のZ-Y-Xのものと同じで起点が +x軸上、北極点が +z軸上)。このように定めることで下右図に示されるように z1-角度を変化させると経度が変化し、y-角度を変化させると緯度が変化し、z2-角度を変化させるとロール角度が変化する。
それぞれの軸周りの回転行列を $R_{z1}$、$R_y$、$R_{z2}$ とすると intrinsic rotations の Z-Y-Zオーダーはこれら3つの回転行列の積として以下のように表される。
\[ R_{zyz} = R_{z1} R_y R_{z2} \]
プログラムにすると以下のように記述される (i_eulZ1、i_eulY、i_eulZ2 は各軸周りの回転角度を表すインスタンス変数であるが、これらを $10^\circ$ ずつ変化させたときの実行結果が上図29である)。
// intrinsic rotations (Z-Y-Z) Matrix4x4 Rz1 = TH3DMath.GetRotation4x4(i_eulZ1, Vecotr3.forward); Matrix4x4 Ry = TH3DMath.GetRotation4x4(i_eulY , Vecotr3.up); Matrix4x4 Rz2 = TH3DMath.GetRotation4x4(i_eulZ2, Vecotr3.forward); Matrix4x4 Rzyz = Rz1 * Ry * Rz2; MiniPlane.SetMatrix(Rzyz);
Z-Y-Zオーダーでは z1-角度の変化は経度の変化につながる。例えば z1-角度 $80^\circ$、y-角度 $70^\circ$、z2-角度 $30^\circ$ はMiniPlane先端が緯度 $20^\circ\ (=90^\circ - 70^\circ)$、経度 $80^\circ$ の位置に置かれ、$30^\circ$ のロール回転をした状態であるが、ここから z1-角度を $10^\circ$ ずつ減少させるとMiniPlane先端が経度 $80^\circ$ の位置から $10^\circ$ ずつ右に移動する (図30)。
図30では z1-角度は $80^\circ$ から $20^\circ$ まで減少するが、図31はそれぞれの状態におけるオイラー角回転の実行過程である。
z1-角度が $10^\circ$ ずつ減少することは、最初の z軸周りの回転角度が $10^\circ$ ずつ減少することを意味するが、それによってMiniPlane先端の置かれる経度が $10^\circ$ ずつ減少する結果となる。
図28に示されるように Z-Y-Zオーダーでは初期状態がジンバルロックの状態から始まる (3つの軸を使用するオイラー角回転ではジンバルロックは緯度を表す角度が $90^\circ$ あるいは $-90^\circ$ のときに起こるが、2つの軸によるオイラー角回転のジンバルロックは緯度を表す角度が $0^\circ$ あるいは $180^\circ$ のときに起こる)。
上で述べたようにジンバルロックの状態では経度の変化とロール角度の変化の区別がつかない。今回は初期状態で z軸プラス方向を向いた状態になっているため、(ローカル座標系の) z軸周りの回転はロール回転になる。しかしジンバルロックの状態では z軸周りの回転をロール角度の変化ではなく経度の変化として扱うことができる。これによって2つの軸しか用いていないにもかかわらず3つの軸を用いた場合と同様の回転を実現できるのである (つまり2つの軸によるオイラー角回転はジンバルロックを利用しているわけである)。
# Code1
本節のアニメーションにおけるMiniPlaneの運動は次のプログラムを実行したものである。[Code1]
// extrinsic rotations: zxy
if (Input.GetKeyDown(KeyCode.X))
{
i_eulX += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Z))
{
i_eulZ += (THUtil.IsShiftDown()) ? -10 : 10;
}
Matrix4x4 R = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ);
MiniPlane.SetMatrix(R);
このプログラムは、Xキー、Yキー、Zキーを押して i_eulX、i_eulY、i_eulZ の値を変化させるもので、1回押すごとに角度が $10^\circ$ ずつ増加する(長押しには対応していない)。また、Shiftキーと同時に押すと角度が $10^\circ$ ずつ減少する (プログラム中の THUtil.IsShiftDown() はShiftキーが押されていればtrueを返すカスタムライブラリのメソッドである)。
なお、このCode1及び次のCode2では x-角度の変更範囲は $-90^\circ$ から $90^\circ$ の範囲に制限してある。つまり、x-角度を押し続けても $90^\circ$ あるいは $-90^\circ$ を越える値にはならない。
プログラム実行中に各キーを押すことで、MiniPlaneの先端が球面上において経線、緯線上を $10^\circ$ ずつ移動したり、あるいは MiniPlaneがそのときいる場所において $10^\circ$ ずつロール回転を行うようになる。
# Code2
Code1では、MiniPlaneの運動はキーを1回1回押さなければいけないものあったが、次のプログラムはキー操作をキーの長押しに変更し、MiniPlaneの運動がなめらかに行われるようにしたものである。[Code2]
// extrinsic rotations: zxy
if (Input.GetKey(KeyCode.X))
{
i_eulX += (THUtil.IsShiftDown()) ? -1 : 1;
}
else if (Input.GetKey(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -1 : 1;
}
else if (Input.GetKey(KeyCode.Z))
{
i_eulZ += (THUtil.IsShiftDown()) ? -1 : 1;
}
Matrix4x4 R = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ);
MiniPlane.SetMatrix(R);
このプログラムは、Code1において Input.GetKeyDown(..) となっていた箇所を Input.GetKey(..) に変え、1フレームあたりの角度の増減を $1^\circ$ ずつに変更しただけである。
# Code3
以下2つのプログラムは intrinsic rotations であり、最初は Z-Y-Xオーダーである。上記と同様に X キー、Y キー、Z キーを押すことでそれぞれの角度が $10^\circ$ ずつ変化する。
[Code3] (実行結果 図25)
// intrinsic rotations: zyx
if (Input.GetKeyDown(KeyCode.X))
{
i_eulX += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Z))
{
i_eulZ += (THUtil.IsShiftDown()) ? -10 : 10;
}
Matrix4x4 Rx = TH3DMath.GetRotation4x4(i_eulX, Vector3.right);
Matrix4x4 Ry = TH3DMath.GetRotation4x4(i_eulY, Vector3.up);
Matrix4x4 Rz = TH3DMath.GetRotation4x4(i_eulZ, Vector3.forward);
Matrix4x4 R = Rz * Ry * Rx;
MiniPlane.SetMatrix(R);
# Code4
intrinsic rotations の Z-Y-Zオーダーのプログラムである。使用するキーは今までと同じであるが、X キーが z1-角度に、Z キーが z2-角度に対応している。
[Code4] (実行結果 図29)
// intrinsic rotations: zyz
if (Input.GetKeyDown(KeyCode.X))
{
i_eulZ1 += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Z))
{
i_eulZ2 += (THUtil.IsShiftDown()) ? -10 : 10;
}
Matrix4x4 Rz1 = TH3DMath.GetRotation4x4(i_eulZ1, Vector3.forward);
Matrix4x4 Ry = TH3DMath.GetRotation4x4(i_eulY, Vector3.up);
Matrix4x4 Rz2 = TH3DMath.GetRotation4x4(i_eulZ2, Vector3.forward);
Matrix4x4 R = Rz1 * Ry * Rz2;
MiniPlane.SetMatrix(R);
© 2020-2024 Redpoll's 60 (All rights reserved)