Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-19
第3章 3D空間の基礎
$§$3-19 応用プログラム 3 (サイコロの回転移動)
前節に引き続き、変換行列の積に関する応用として本節では立方体の回転移動の問題について扱う。本節における「立方体の回転移動」とは、立方体が図1に示されるように平面上を回転しながら移動していくことを意味する。
まずは、この回転移動について見ていく。

図1 立方体の回転移動 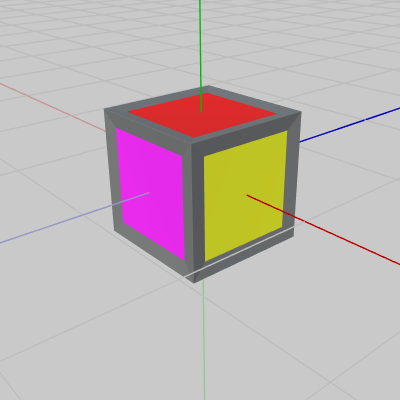
図2 立方体 初期状態
図2はここで使用する立方体の初期状態である。立方体の各辺の長さは $1$ で、初期状態ではその中心が原点に置かれている。また、初期状態では立方体の黄色い面が x軸プラス方向を向いており、赤い面が真上(y軸プラス方向)を向いている。
下図3は立方体をXZ平面上に置いたときのものであるが、このときの立方体の中心位置を $P$ とする。図4はこの立方体を図Bの位置から x軸に沿って図5のように 1マス分回転移動させたときのものであるが、このときの立方体の中心位置を $Q$ とする (図3、図4における白い小球が立方体の中心を表している)。
この 1マス分の回転移動は図3に示される辺$AB$を回転軸とする回転と見ることもできる。辺$AB$は z軸に平行であり、$A = (3, 0, 0)$、$B = (3, 0, 1)$ である。
次のプログラムは立方体を $P$ から $Q$ まで、つまり 図Bの位置から図Cの位置まで x軸に沿って1マス分 回転移動させるものである。
なお、以降のプログラムでは立方体は Cube という名前で使われている。
[BetaA] (実行結果 図5)
このプログラムでは Sキーが押されると 1行目のifブロックに入るが、ここで各インスタンス変数を初期化する。i_MOVE はbool型の変数で初期値はfalseであり、Sキーが押されるとtrueになる。この変数がfalseの間は9行目以降の回転移動の部分に処理が進まない。
立方体の 1マス分の回転移動は60フレームかけて行われる。i_motionCounter はint型の変数で、その60フレームかけて行われる回転移動において何フレーム目かを表す変数である。Sキーが押されると i_motionCounter は $0$ にリセットされるが、回転移動中には11行目において毎フレーム $1$ ずつ増加する。移動開始後、60フレーム経過するとこの変数の値が $60$ になるが、その際には28行目のifブロックに入ることになり i_MOVE がfalseになる。これによって回転移動が終了し、再度 Sキーが押されるまで停止した状態が続く。
5行目の i_curRotation については後述する。
また、6行目では立方体に平行移動を実行しているが、この平行移動によって立方体は図3に示される移動開始前の位置 $P$ に移動する。
今回の1マス分の移動は60フレームかけて行われるが、60フレームの間に立方体は図5に示されるように位置と向きが変化する。立方体に実行される変換は回転行列と平行移動行列の積であり、平行移動行列の内容が毎フレーム変化するので位置の変化が生じ、回転行列の内容が毎フレーム変化するので向きの変化が生じる。
例えば、立方体の向きについていえば、移動前の立方体は黄色い面が x軸プラス方向を向いており、赤い面が真上を向いているが、移動後では 黄色い面は下になり、赤い面が x軸プラス方向を向くようになる。この場合の立方体の向きの変化は単に $90^\circ$ の回転をしているに過ぎない。
次のプログラムは上記のBetaAにおいて $P$ から $Q$ への移動を行わないようにし、立方体の向きだけが変化するようにしたものである (立方体の位置は $P$ から変化しない)。
[BetaB] (実行結果 図6)
このプログラムは先程のBetaAの16行目から21行目を
Matrix4x4 T = TH3DMath.GetTranslation4x4(P) に変えただけである (16行目)。この変更によって立方体は $P$ から $Q$ への移動ではなく、常に $P$ に置かれ続ける。
実行結果(図6)に見られるように、立方体は $P$ の位置において向きだけが変化する。

図6 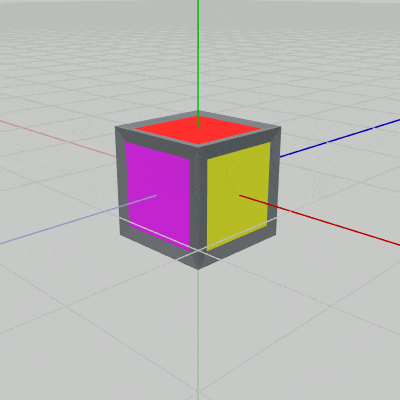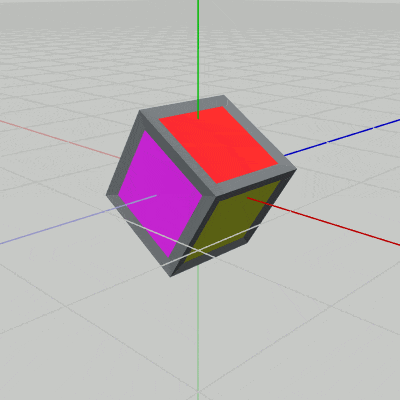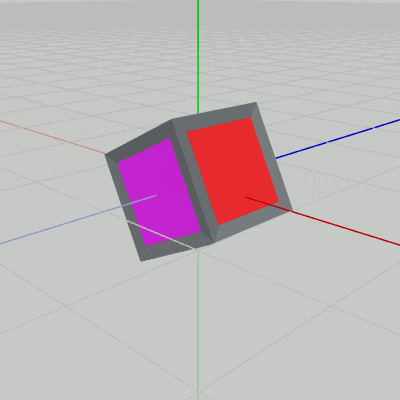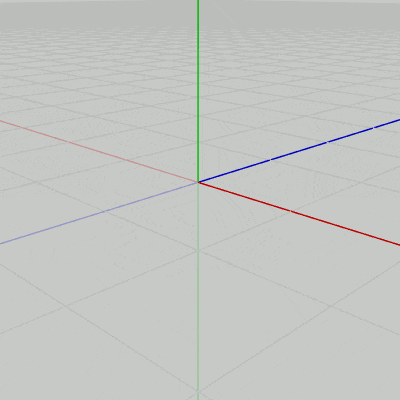
図7
BetaBは立方体の移動先が毎フレーム $P$ であるため、$P$ において向きの変化だけが起こる。もし、この $P$ への移動も行わないようにした場合、すなわち、16行目の平行移動行列の内容を TH3DMath.GetTranslation4x4(0, 0, 0) にするか、あるいは立方体に実行する18行目の変換行列 mtx を mtx = T * R ではなく mtx = R とした場合、立方体は初期状態の位置から位置が変化しないため、図7に示されるように原点において向きだけが変化する。そして、この向きの変化は z軸マイナス方向を回転軸とする $90^\circ$ の回転である (z軸プラス方向を回転軸にする場合は $-90^\circ$ の回転である)。
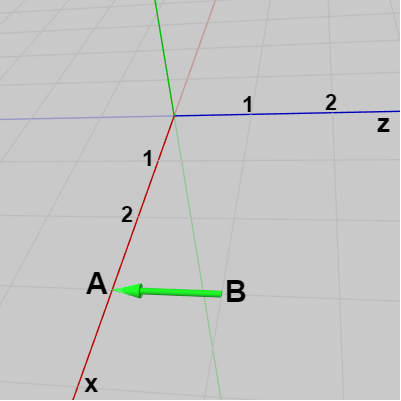
図8 ベクトルBAは z軸マイナス方向 プログラム13行目の axis は回転軸を表すが、ここでは axis = A - B となっている。上でも述べたように辺$AB$は z軸に平行であるが、回転軸を z軸マイナス方向にするためには、回転軸は $\overrightarrow{BA} (= A - B)$ を使う必要がある。具体的な座標で表すと $A = (3, 0, 0)$、$B = (3, 0, 1)$ であるから\[ \overrightarrow{BA} = A - B = (3, 0, 0) - (3, 0, 1) = (0, 0, -1)\]となる (図8)。
立方体の 1マス分の回転移動は60フレームかけて行われるが、その間に立方体は $90^\circ$ 回転する。したがって、1フレームあたり $1.5^\circ$ 回転するわけであるが、14行目の wr はこの $1.5^\circ$ の回転を表す回転行列である (wrの内容は毎フレーム同じ)。
BetaBでは立方体の移動先が毎フレーム $P$ であるため、16行目の平行移動行列 T の内容は $P$ への平行移動であり、これは毎フレーム変わらない。17行目の回転行列 R は R = wr * i_curRotation となっているが、これによって60フレームの間に $-z$ 軸周りに $90^\circ$ の回転が行われる。
i_curRotation は立方体の現在の回転状態を表す行列で、これは Matrix4x4型のインスタンス変数であり、初期値は(回転移動の開始前は) identity行列である。
この i_curRotation には毎フレーム 21行目で R の内容がコピーされる。したがって、17行目の R = wr * i_curRotation における i_curRotation の内容は1フレーム前の R の内容である。
例えば、回転移動を開始したときの最初のフレーム(1フレーム目とする)では、i_curRotation の内容は identity行列であり、wr は $-z$ 軸周りの $1.5^\circ$ の回転行列であるから、17行目で計算される R の内容は「$-z$ 軸周りの $1.5^\circ$ の回転」である。そして、21行目において i_curRotation にはこの R の内容がコピーされる。
2フレーム目では、i_curRotation の内容は「$-z$ 軸周りの $1.5^\circ$ の回転」になっているから、17行目で計算される R の内容は、i_curRotation をさらに $-z$ 軸周りに $1.5^\circ$ 回転させた「$-z$ 軸周りの $3^\circ$ の回転」になる。
3フレーム目も同様である。3フレーム目では i_curRotation の内容は「$-z$ 軸周りの $3^\circ$ の回転」になっているから、17行目で計算される R の内容は、i_curRotation をさらに $-z$ 軸周りに $1.5^\circ$ 回転させた「$-z$ 軸周りの $4.5^\circ$ の回転」になる。
それ以降も同様であり、これを60フレーム繰り返すことによって立方体を $-z$ 軸周りに $90^\circ$ 回転させるわけである。BetaBでは毎フレーム、回転後に $P$ への平行移動が行われるため、BetaBの実行結果に見られるように、立方体は $P$ において $90^\circ$ 回転することになる。
(3-17節のルービックキューブのプログラムも同様の処理であったが、そこでは各Cubeの現在の回転状態を取得するために GetMatrix() というメソッドを使っていた。このメソッドは前のフレームにおいて SetMatrix(..) にセットした行列が返される。今回のプログラムで、この GetMatrix() を使わずに i_curRotation というインスタンス変数を用意しているのは、今回のプログラムにおいては立方体に対して回転だけでなく平行移動が行われるためである。3-17節のルービックキューブのプログラムでは各Cubeに対して実行される変換は回転のみであったので、各Cubeの現在の回転状態を取得するために GetMatrix() を使うことができたのである。もし、今回のプログラムで GetMatrix() を使うのであれば、GetMatrix() によって取得した行列の第4列目の x座標、y座標、z座標を $0$ にして、行列から平行移動成分を消去する必要がある。詳しくは 4-6節参照)
次に、$P$ から $Q$ への回転移動における位置の変化について見ていく。
下図9はBetaAの実行結果を視点を変えて見たときのものである。
この1マス分の移動において、立方体の中心は $P$ から $Q$ へ移動するわけであるが、この移動経路は $90^\circ$ 分の円周上の移動である。具体的には、辺$AB$の中点を $M$ とし(図10)、回転軸を $\overrightarrow{BA}$ とするとき、$P$ を $M$ の周りに $90^\circ$ 回転させたときにできる弧が立方体の中心の移動経路である (図11に示されるように $\angle{PMQ} = 90^\circ$ である)。
以下はBetaAの16~19行目の部分であるが、これはこの $90^\circ$ 分の円周上の各位置を計算しているのである。60フレームで $90^\circ$ 分の移動を行うので、毎フレーム この円周上を $1.5^\circ$ ずつ進んでいく。
(このコードについての解説は 3-10節 Code3 参照。そこでは同様の問題が扱われている。)
上記では立方体の $P$ から $Q$ までの 1マス分の回転移動について、位置の変化と向きの変化に分けてやや詳しく見てきたが、この立方体をさらに続けて回転移動させる場合も考え方は同じである。
例えば $Q$ に移動した状態から下図12に示されるように、さらに z軸プラス方向へ 1マス分だけ回転移動させるとしよう。移動前の状態が図13であり、移動後の状態が図14である。図14における $R$ は移動後の立方体の中心を表している。
このときの位置の変化、すなわち 立方体中心の移動経路は、辺$BC$の中点を $N$ とし(下図15)、回転軸を $\overrightarrow{BC}$ とするとき、$Q$ を $N$ の周りに $90^\circ$ 回転させたときにできる弧である (図16に示されるように $\angle{QNR} = 90^\circ$ である)。
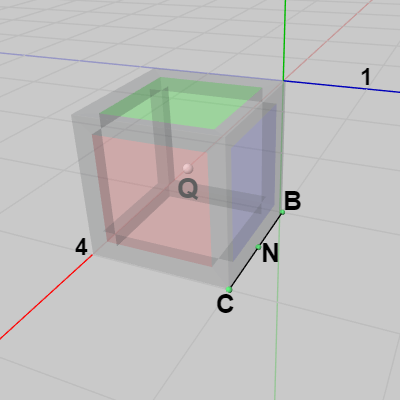
図15 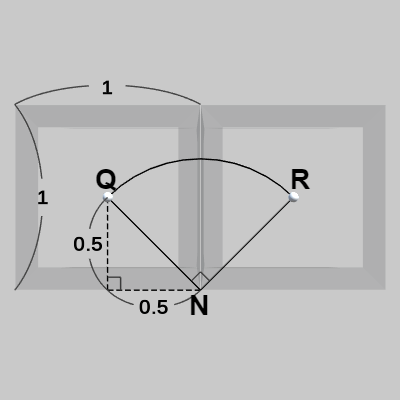
図16
$B$、$C$ の具体的な座標は $B = (3, 0, 1)$、$C = (4, 0, 1)$ であり、回転軸 $\overrightarrow{BC}$ は\[ \overrightarrow{BC} = C - B = (4, 0, 1) - (3, 0, 1) = (1, 0, 0)\]となる。$\overrightarrow{BC}$ は x軸に平行である。
上図12のアニメーションに示されるように、この回転移動によって立方体の青い面が下になり、緑の面が z軸プラス方向を向くことになる。したがって、向きの変化は立方体を $Q$ の位置から原点に戻して考えると、$Q$ から $R$ への回転移動では、立方体を最初の回転移動が終わった状態から x軸周りに $90^\circ$ 回転させることに相当する。
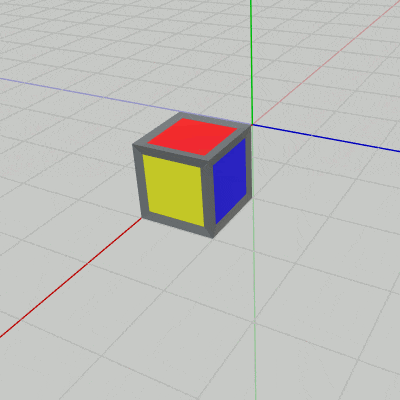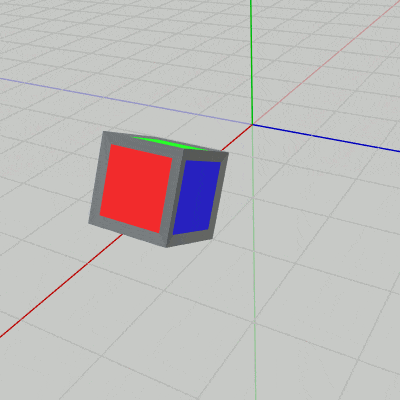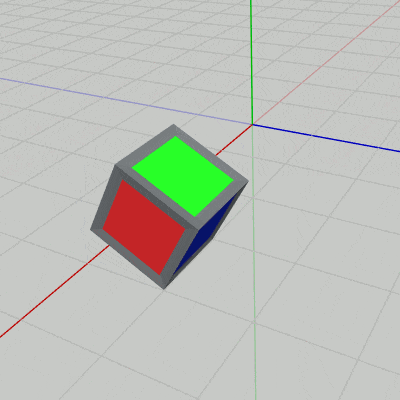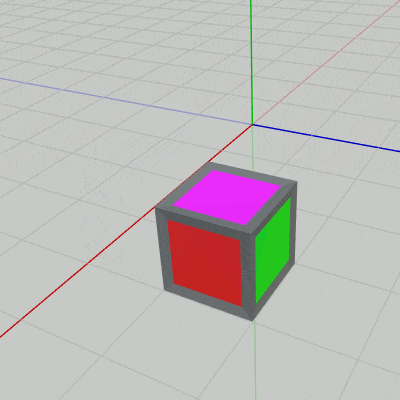
図17 PからQ、QからRへ続けて移動する 最初の回転移動が終わった時点では立方体の向きは、黄色い面が下になり、赤い面が x軸プラス方向を向くことになる。上図7で示したように、これは原点に戻して見た場合には $-z$ 軸周りの $90^\circ$ の回転である。
これに続く $Q$ から $R$ へ回転移動において、立方体の向きの変化は(原点に戻して見た場合)、最初の回転移動が終わった状態から x軸周りに $90^\circ$ 回転させなければならないということである。
右図17は上記の $P$ から $Q$ への回転移動、及び $Q$ から $R$ への回転移動を続けて行ったときのものである。
以上をふまえて、立方体の回転移動に関するプログラムを作成するが、このプログラムは読者用の課題である。
「サイコロが下図に示されるA地点に置かれており、このときのサイコロの上の面の数字は 3 である。今、A地点から図に示される経路に沿ってサイコロをB地点までころがしていくとき、B地点に着いたときのサイコロの上の面の数字は何になっているか」
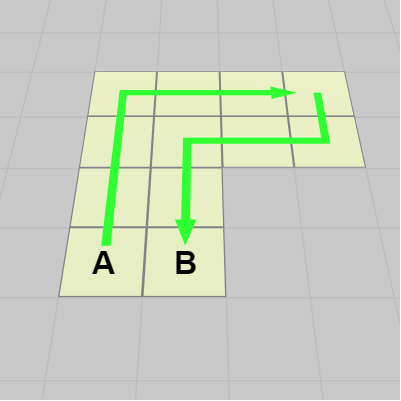
図18 
図19
ここでの読者の課題は、実際にサイコロを上図のA地点から経路に沿ってB地点までころがしていき、B地点に着いたときにサイコロの上の面の数字が何になっているかを確認するプログラムの作成である。
プログラムで使用するサイコロは図20のオブジェクト Dice である。Diceは上記の解説で使われた立方体と同じく、各辺の長さが $1$ の立方体で、初期状態ではその中心が原点に置かれている。
また、図21に示されるようにサイコロの進むマス目は 1辺の長さが $1$ の正方形であり、これはサイコロの各辺の長さと同じである。

図20 Dice 初期状態 
図21 各マス目は1辺の長さ 1 の正方形 (サイコロの1辺の長さと同じ)
このプログラムに用意されているインスタンス変数、及び定数は以下のとおり。
この変数はサイコロが現在どのマス目にいるのかを表すためのものである。
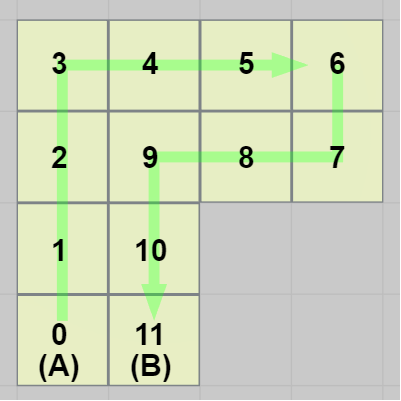
図22 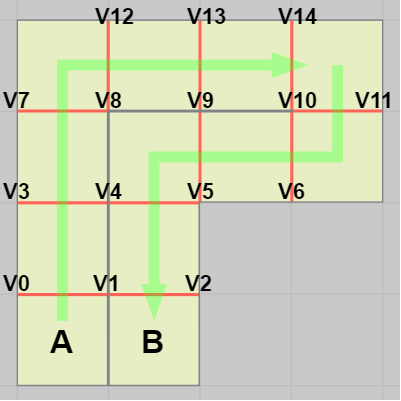
図23
サイコロの移動経路は12のマス目によって構成されているが、サイコロがA地点から出発してB地点に至るまでに行う回転移動の回数は 11回である。そして、その間に通過する辺の数も同じく 11 である。
i_edgeList にはサイコロがA地点からB地点に至るまでに通過する11個の辺が、通過する順番でセットされている。
辺は2つの Vector3 によって表されるので、i_edgeList の各要素は2つの Vector3 から成る配列である。具体的には、以下のような値がセットされている (以下で使われている V[0] ~ V14 は上図23の $V0$ ~ $V14$ と同じもので、各辺の両端の頂点座標である)。
上図22の番号を使えば、サイコロは最初の移動で「0」から「1」に移動するが、このとき通過する辺は $V0V1$ である(図23)。次の移動では(図22における)「1」から「2」に移動するが、このとき通過する辺は $V3V4$ である(図23)。
このように、i_edgeList にはA地点からB地点に至るまでに通過する11個の辺が、通過する順番でセットされているのである。
i_edgeList の要素を取り出す際は以下のように記述すればよい。
この例では i_edgeList の先頭から数えて3番目の要素を取り出しているが、その内容は辺$V7V8$を構成する2つの頂点座標であり、edge[0] が $V7$ の座標、edge[1] が $V8$ の座標である。
プログラムの作成はCode1に行うものとする。Code1は最初の段階では以下のコードのみが記述されている。このまま実行するとサイコロがA地点に置かれた状態、すなわち出発時の状態(図19)になる。
[Code1]
プログラム 5行目の A は上で述べたVector3型の定数で、初期状態のDiceに対して A だけの平行移動を実行すると DiceはA地点に置かれた状態になる (出発時点においてはDiceの向きは初期状態と同じであるので、DiceをA地点まで平行移動させる際にDiceの向きを変える必要はない)。
また、このプログラムでは Sキーを押すことによってサイコロの回転移動を始めるものとする。
本節前半のプログラム BetaA は 1マス分の回転移動であったが、ここではそれが複数回行われるだけであり、回転移動の処理自体は同じものである。したがって、この課題はBetaAにいくつかの追加をすれば解決する (サイコロをころがす問題を算数的に解く際には、サイコロの向かい合う面の数字の和が $7$ になるという情報が重要な手がかりになるが、このプログラムを作成する際にはそういった情報は必要ではない)。
プログラムの解答例については Sec319_Ans.txt を参照 (Sec319_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
オブジェクトに対して実行する変換がスケール、回転、平行移動である場合、その順序はスケール、回転、平行移動の順で行うようにする。これはコンピューターグラフィックスにおける基本である。
第5章で解説するが、Unityの標準的な変換方法(「Position」「Rotation」「Scale」に値を設定する方法)においても、その実行順序は常にスケール、回転、平行移動の順で行われる。
本節で扱った立方体の回転移動と4-1節で扱う球体の自転と公転は、コンピューターグラフィックスにおける単一のオブジェクトの運動としては最も重要な例である。この2つの問題はコンピューターグラフィックスにおいてオブジェクトを動かす際には、どのように考えるのかということを端的に表している。こういった運動を何度も実装していくうちにスケール、回転、平行移動の順で変換を考える習慣が身に付くのである (そして、そういった考え方が自然であると感じるようになるのである)。
コンピューターグラフィックスにおけるオブジェクトの運動は、まず原点において指定の大きさにスケールし、次に指定の向きに(厳密には指定のOrientationに)回転させ、最後に指定の位置まで移動させる。これを毎フレーム繰り返すことによって実現されるのである。
まずは、この回転移動について見ていく。


図2はここで使用する立方体の初期状態である。立方体の各辺の長さは $1$ で、初期状態ではその中心が原点に置かれている。また、初期状態では立方体の黄色い面が x軸プラス方向を向いており、赤い面が真上(y軸プラス方向)を向いている。
下図3は立方体をXZ平面上に置いたときのものであるが、このときの立方体の中心位置を $P$ とする。図4はこの立方体を図Bの位置から x軸に沿って図5のように 1マス分回転移動させたときのものであるが、このときの立方体の中心位置を $Q$ とする (図3、図4における白い小球が立方体の中心を表している)。
この 1マス分の回転移動は図3に示される辺$AB$を回転軸とする回転と見ることもできる。辺$AB$は z軸に平行であり、$A = (3, 0, 0)$、$B = (3, 0, 1)$ である。
-
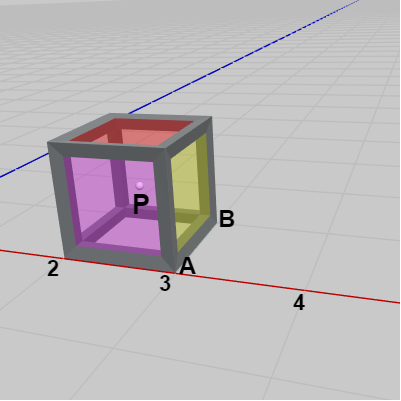 図3
図3 -
 図4
図4 -
 図5 x軸プラス方向への1マス分の移動 (PからQへの移動)
図5 x軸プラス方向への1マス分の移動 (PからQへの移動)
次のプログラムは立方体を $P$ から $Q$ まで、つまり 図Bの位置から図Cの位置まで x軸に沿って1マス分 回転移動させるものである。
なお、以降のプログラムでは立方体は Cube という名前で使われている。
[BetaA] (実行結果 図5)
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = true;
i_motionCounter = 0;
i_curRotation = Matrix4x4.identity;
Cube.SetMatrix(TH3DMath.GetTranslation4x4(P));
}
if (!i_MOVE) { return; }
i_motionCounter++;
Vector3 axis = A - B;
Matrix4x4 wr = TH3DMath.GetRotation4x4(90.0f / 60, axis);
Vector3 M = (A + B) * 0.5f;
Vector3 wp = Cube.GetWorldPosition();
Vector3 pos = wr * TH3DMath.ToVector4(wp - M);
pos += M;
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
Matrix4x4 R = wr * i_curRotation;
Matrix4x4 mtx = T * R;
Cube.SetMatrix(mtx);
i_curRotation = R;
if (i_motionCounter >= 60)
{
i_MOVE = false;
}
このプログラムでは Sキーが押されると 1行目のifブロックに入るが、ここで各インスタンス変数を初期化する。i_MOVE はbool型の変数で初期値はfalseであり、Sキーが押されるとtrueになる。この変数がfalseの間は9行目以降の回転移動の部分に処理が進まない。
立方体の 1マス分の回転移動は60フレームかけて行われる。i_motionCounter はint型の変数で、その60フレームかけて行われる回転移動において何フレーム目かを表す変数である。Sキーが押されると i_motionCounter は $0$ にリセットされるが、回転移動中には11行目において毎フレーム $1$ ずつ増加する。移動開始後、60フレーム経過するとこの変数の値が $60$ になるが、その際には28行目のifブロックに入ることになり i_MOVE がfalseになる。これによって回転移動が終了し、再度 Sキーが押されるまで停止した状態が続く。
5行目の i_curRotation については後述する。
また、6行目では立方体に平行移動を実行しているが、この平行移動によって立方体は図3に示される移動開始前の位置 $P$ に移動する。
今回の1マス分の移動は60フレームかけて行われるが、60フレームの間に立方体は図5に示されるように位置と向きが変化する。立方体に実行される変換は回転行列と平行移動行列の積であり、平行移動行列の内容が毎フレーム変化するので位置の変化が生じ、回転行列の内容が毎フレーム変化するので向きの変化が生じる。
例えば、立方体の向きについていえば、移動前の立方体は黄色い面が x軸プラス方向を向いており、赤い面が真上を向いているが、移動後では 黄色い面は下になり、赤い面が x軸プラス方向を向くようになる。この場合の立方体の向きの変化は単に $90^\circ$ の回転をしているに過ぎない。
次のプログラムは上記のBetaAにおいて $P$ から $Q$ への移動を行わないようにし、立方体の向きだけが変化するようにしたものである (立方体の位置は $P$ から変化しない)。
[BetaB] (実行結果 図6)
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = true;
i_motionCounter = 0;
i_curRotation = Matrix4x4.identity;
Cube.SetMatrix(TH3DMath.GetTranslation4x4(P));
}
if (!i_MOVE) { return; }
i_motionCounter++;
Vector3 axis = A - B;
Matrix4x4 wr = TH3DMath.GetRotation4x4(90.0f / 60, axis);
Matrix4x4 T = TH3DMath.GetTranslation4x4(P);
Matrix4x4 R = wr * i_curRotation;
Matrix4x4 mtx = T * R;
Cube.SetMatrix(mtx);
i_curRotation = R;
if (i_motionCounter >= 60)
{
i_MOVE = false;
}
このプログラムは先程のBetaAの16行目から21行目を
Matrix4x4 T = TH3DMath.GetTranslation4x4(P) に変えただけである (16行目)。この変更によって立方体は $P$ から $Q$ への移動ではなく、常に $P$ に置かれ続ける。
実行結果(図6)に見られるように、立方体は $P$ の位置において向きだけが変化する。


BetaBは立方体の移動先が毎フレーム $P$ であるため、$P$ において向きの変化だけが起こる。もし、この $P$ への移動も行わないようにした場合、すなわち、16行目の平行移動行列の内容を TH3DMath.GetTranslation4x4(0, 0, 0) にするか、あるいは立方体に実行する18行目の変換行列 mtx を mtx = T * R ではなく mtx = R とした場合、立方体は初期状態の位置から位置が変化しないため、図7に示されるように原点において向きだけが変化する。そして、この向きの変化は z軸マイナス方向を回転軸とする $90^\circ$ の回転である (z軸プラス方向を回転軸にする場合は $-90^\circ$ の回転である)。

立方体の 1マス分の回転移動は60フレームかけて行われるが、その間に立方体は $90^\circ$ 回転する。したがって、1フレームあたり $1.5^\circ$ 回転するわけであるが、14行目の wr はこの $1.5^\circ$ の回転を表す回転行列である (wrの内容は毎フレーム同じ)。
BetaBでは立方体の移動先が毎フレーム $P$ であるため、16行目の平行移動行列 T の内容は $P$ への平行移動であり、これは毎フレーム変わらない。17行目の回転行列 R は R = wr * i_curRotation となっているが、これによって60フレームの間に $-z$ 軸周りに $90^\circ$ の回転が行われる。
i_curRotation は立方体の現在の回転状態を表す行列で、これは Matrix4x4型のインスタンス変数であり、初期値は(回転移動の開始前は) identity行列である。
この i_curRotation には毎フレーム 21行目で R の内容がコピーされる。したがって、17行目の R = wr * i_curRotation における i_curRotation の内容は1フレーム前の R の内容である。
例えば、回転移動を開始したときの最初のフレーム(1フレーム目とする)では、i_curRotation の内容は identity行列であり、wr は $-z$ 軸周りの $1.5^\circ$ の回転行列であるから、17行目で計算される R の内容は「$-z$ 軸周りの $1.5^\circ$ の回転」である。そして、21行目において i_curRotation にはこの R の内容がコピーされる。
2フレーム目では、i_curRotation の内容は「$-z$ 軸周りの $1.5^\circ$ の回転」になっているから、17行目で計算される R の内容は、i_curRotation をさらに $-z$ 軸周りに $1.5^\circ$ 回転させた「$-z$ 軸周りの $3^\circ$ の回転」になる。
3フレーム目も同様である。3フレーム目では i_curRotation の内容は「$-z$ 軸周りの $3^\circ$ の回転」になっているから、17行目で計算される R の内容は、i_curRotation をさらに $-z$ 軸周りに $1.5^\circ$ 回転させた「$-z$ 軸周りの $4.5^\circ$ の回転」になる。
それ以降も同様であり、これを60フレーム繰り返すことによって立方体を $-z$ 軸周りに $90^\circ$ 回転させるわけである。BetaBでは毎フレーム、回転後に $P$ への平行移動が行われるため、BetaBの実行結果に見られるように、立方体は $P$ において $90^\circ$ 回転することになる。
(3-17節のルービックキューブのプログラムも同様の処理であったが、そこでは各Cubeの現在の回転状態を取得するために GetMatrix() というメソッドを使っていた。このメソッドは前のフレームにおいて SetMatrix(..) にセットした行列が返される。今回のプログラムで、この GetMatrix() を使わずに i_curRotation というインスタンス変数を用意しているのは、今回のプログラムにおいては立方体に対して回転だけでなく平行移動が行われるためである。3-17節のルービックキューブのプログラムでは各Cubeに対して実行される変換は回転のみであったので、各Cubeの現在の回転状態を取得するために GetMatrix() を使うことができたのである。もし、今回のプログラムで GetMatrix() を使うのであれば、GetMatrix() によって取得した行列の第4列目の x座標、y座標、z座標を $0$ にして、行列から平行移動成分を消去する必要がある。詳しくは 4-6節参照)
次に、$P$ から $Q$ への回転移動における位置の変化について見ていく。
下図9はBetaAの実行結果を視点を変えて見たときのものである。
-
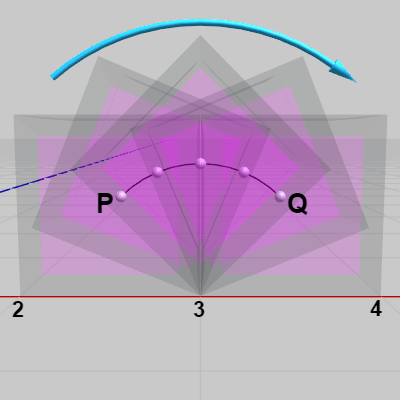 図9
図9 -
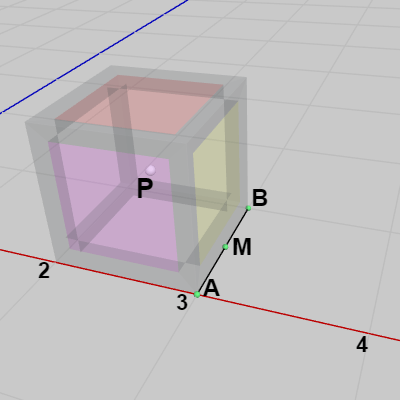 図10
図10 -
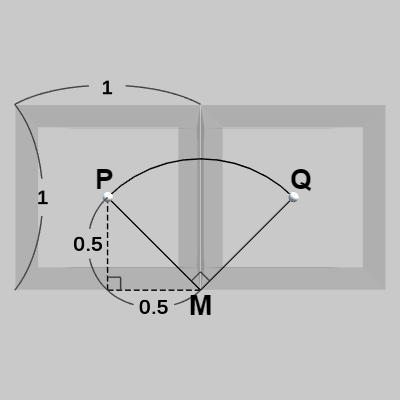 図11
図11
この1マス分の移動において、立方体の中心は $P$ から $Q$ へ移動するわけであるが、この移動経路は $90^\circ$ 分の円周上の移動である。具体的には、辺$AB$の中点を $M$ とし(図10)、回転軸を $\overrightarrow{BA}$ とするとき、$P$ を $M$ の周りに $90^\circ$ 回転させたときにできる弧が立方体の中心の移動経路である (図11に示されるように $\angle{PMQ} = 90^\circ$ である)。
以下はBetaAの16~19行目の部分であるが、これはこの $90^\circ$ 分の円周上の各位置を計算しているのである。60フレームで $90^\circ$ 分の移動を行うので、毎フレーム この円周上を $1.5^\circ$ ずつ進んでいく。
Vector3 M = (A + B) * 0.5f; Vector3 wp = Cube.GetWorldPosition(); Vector3 pos = wr * TH3DMath.ToVector4(wp - M); pos += M;
上記では立方体の $P$ から $Q$ までの 1マス分の回転移動について、位置の変化と向きの変化に分けてやや詳しく見てきたが、この立方体をさらに続けて回転移動させる場合も考え方は同じである。
例えば $Q$ に移動した状態から下図12に示されるように、さらに z軸プラス方向へ 1マス分だけ回転移動させるとしよう。移動前の状態が図13であり、移動後の状態が図14である。図14における $R$ は移動後の立方体の中心を表している。
-
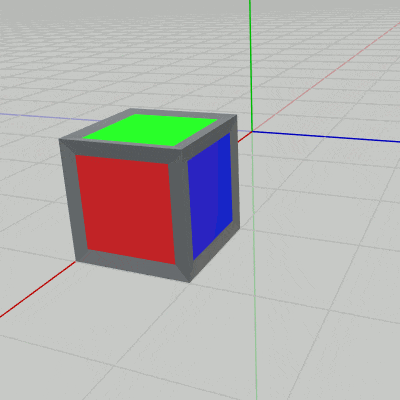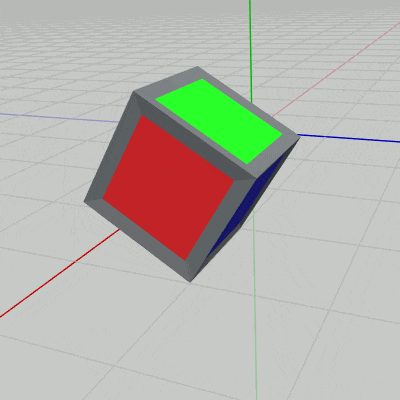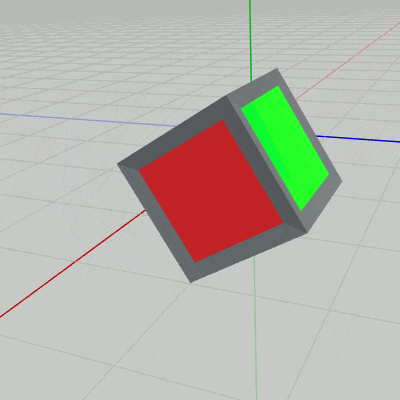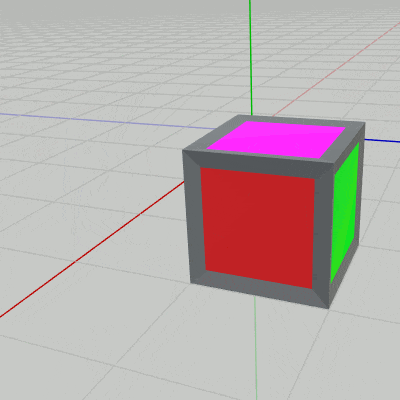 図12 z軸プラス方向への1マス分の移動 (QからRへの移動)
図12 z軸プラス方向への1マス分の移動 (QからRへの移動) -
 図13 移動前(Qは立方体の中心)
図13 移動前(Qは立方体の中心) -
 図14 移動後(Rは立方体の中心)
図14 移動後(Rは立方体の中心)
このときの位置の変化、すなわち 立方体中心の移動経路は、辺$BC$の中点を $N$ とし(下図15)、回転軸を $\overrightarrow{BC}$ とするとき、$Q$ を $N$ の周りに $90^\circ$ 回転させたときにできる弧である (図16に示されるように $\angle{QNR} = 90^\circ$ である)。


$B$、$C$ の具体的な座標は $B = (3, 0, 1)$、$C = (4, 0, 1)$ であり、回転軸 $\overrightarrow{BC}$ は\[ \overrightarrow{BC} = C - B = (4, 0, 1) - (3, 0, 1) = (1, 0, 0)\]となる。$\overrightarrow{BC}$ は x軸に平行である。
上図12のアニメーションに示されるように、この回転移動によって立方体の青い面が下になり、緑の面が z軸プラス方向を向くことになる。したがって、向きの変化は立方体を $Q$ の位置から原点に戻して考えると、$Q$ から $R$ への回転移動では、立方体を最初の回転移動が終わった状態から x軸周りに $90^\circ$ 回転させることに相当する。

これに続く $Q$ から $R$ へ回転移動において、立方体の向きの変化は(原点に戻して見た場合)、最初の回転移動が終わった状態から x軸周りに $90^\circ$ 回転させなければならないということである。
右図17は上記の $P$ から $Q$ への回転移動、及び $Q$ から $R$ への回転移動を続けて行ったときのものである。
以上をふまえて、立方体の回転移動に関するプログラムを作成するが、このプログラムは読者用の課題である。
# Code1
中学受験の入試問題などではサイコロをころがす問題が出されることがある。例えば、それは次のようなものである。「サイコロが下図に示されるA地点に置かれており、このときのサイコロの上の面の数字は 3 である。今、A地点から図に示される経路に沿ってサイコロをB地点までころがしていくとき、B地点に着いたときのサイコロの上の面の数字は何になっているか」


ここでの読者の課題は、実際にサイコロを上図のA地点から経路に沿ってB地点までころがしていき、B地点に着いたときにサイコロの上の面の数字が何になっているかを確認するプログラムの作成である。
プログラムで使用するサイコロは図20のオブジェクト Dice である。Diceは上記の解説で使われた立方体と同じく、各辺の長さが $1$ の立方体で、初期状態ではその中心が原点に置かれている。
また、図21に示されるようにサイコロの進むマス目は 1辺の長さが $1$ の正方形であり、これはサイコロの各辺の長さと同じである。


このプログラムに用意されているインスタンス変数、及び定数は以下のとおり。
A
: サイコロをA地点へ移動させるためのVector3型の定数。サイコロをA地点に移動させるには、初期状態のDiceに対してこの定数を用いた平行移動を実行すればよい (以下のプログラム参照)。i_MOVE, i_motionCounter, i_curRotation
: これらのインスタンス変数の役割については本節の前半の解説で述べた通りである。i_curSquare
: int型のインスタンス変数である。サイコロの移動経路となるマス目は下図22に示されるように12個あり、各マス目には図に示される番号が割り当てられている。例えば、A地点ならば「0」、B地点ならば「11」である。この変数はサイコロが現在どのマス目にいるのかを表すためのものである。


i_edgeList
: List型のインスタンス変数であり、その要素は Vector3型の配列である。サイコロの移動経路は12のマス目によって構成されているが、サイコロがA地点から出発してB地点に至るまでに行う回転移動の回数は 11回である。そして、その間に通過する辺の数も同じく 11 である。
i_edgeList にはサイコロがA地点からB地点に至るまでに通過する11個の辺が、通過する順番でセットされている。
辺は2つの Vector3 によって表されるので、i_edgeList の各要素は2つの Vector3 から成る配列である。具体的には、以下のような値がセットされている (以下で使われている V[0] ~ V14 は上図23の $V0$ ~ $V14$ と同じもので、各辺の両端の頂点座標である)。
i_edgeList = new List<Vector3[]>()
{
new Vector3[]{ V[0], V[1] },
new Vector3[]{ V[3], V[4] },
new Vector3[]{ V[7], V[8] },
new Vector3[]{ V[12], V[8] },
new Vector3[]{ V[13], V[9] },
new Vector3[]{ V[14], V[10] },
new Vector3[]{ V[11], V[10] },
new Vector3[]{ V[6], V[10] },
new Vector3[]{ V[5], V[9] },
new Vector3[]{ V[5], V[4] },
new Vector3[]{ V[2], V[1] }
};
上図22の番号を使えば、サイコロは最初の移動で「0」から「1」に移動するが、このとき通過する辺は $V0V1$ である(図23)。次の移動では(図22における)「1」から「2」に移動するが、このとき通過する辺は $V3V4$ である(図23)。
このように、i_edgeList にはA地点からB地点に至るまでに通過する11個の辺が、通過する順番でセットされているのである。
i_edgeList の要素を取り出す際は以下のように記述すればよい。
Vector3[] edge = i_edgeList[2]; Vector3 A = edge[0]; Vector3 B = edge[1];
プログラムの作成はCode1に行うものとする。Code1は最初の段階では以下のコードのみが記述されている。このまま実行するとサイコロがA地点に置かれた状態、すなわち出発時の状態(図19)になる。
[Code1]
void Code1()
{
if (!i_INITIALIZED)
{
Dice.SetMatrix(TH3DMath.GetTranslation4x4(A));
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = true;
}
if (!i_MOVE) { return; }
}
プログラム 5行目の A は上で述べたVector3型の定数で、初期状態のDiceに対して A だけの平行移動を実行すると DiceはA地点に置かれた状態になる (出発時点においてはDiceの向きは初期状態と同じであるので、DiceをA地点まで平行移動させる際にDiceの向きを変える必要はない)。
また、このプログラムでは Sキーを押すことによってサイコロの回転移動を始めるものとする。
本節前半のプログラム BetaA は 1マス分の回転移動であったが、ここではそれが複数回行われるだけであり、回転移動の処理自体は同じものである。したがって、この課題はBetaAにいくつかの追加をすれば解決する (サイコロをころがす問題を算数的に解く際には、サイコロの向かい合う面の数字の和が $7$ になるという情報が重要な手がかりになるが、このプログラムを作成する際にはそういった情報は必要ではない)。
プログラムの解答例については Sec319_Ans.txt を参照 (Sec319_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
オブジェクトに対して実行する変換がスケール、回転、平行移動である場合、その順序はスケール、回転、平行移動の順で行うようにする。これはコンピューターグラフィックスにおける基本である。
第5章で解説するが、Unityの標準的な変換方法(「Position」「Rotation」「Scale」に値を設定する方法)においても、その実行順序は常にスケール、回転、平行移動の順で行われる。
本節で扱った立方体の回転移動と4-1節で扱う球体の自転と公転は、コンピューターグラフィックスにおける単一のオブジェクトの運動としては最も重要な例である。この2つの問題はコンピューターグラフィックスにおいてオブジェクトを動かす際には、どのように考えるのかということを端的に表している。こういった運動を何度も実装していくうちにスケール、回転、平行移動の順で変換を考える習慣が身に付くのである (そして、そういった考え方が自然であると感じるようになるのである)。
コンピューターグラフィックスにおけるオブジェクトの運動は、まず原点において指定の大きさにスケールし、次に指定の向きに(厳密には指定のOrientationに)回転させ、最後に指定の位置まで移動させる。これを毎フレーム繰り返すことによって実現されるのである。
© 2020-2025 Redpoll's 60 (All rights reserved)