Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-2
第3章 3D空間の基礎
$§$3-2 ベクトルによる平行移動
本節では3D空間上の点にベクトルを加算することによって別の地点に移動(より正確には平行移動)させる問題を扱う。内容としては1-2節、1-3節の3D空間への拡張版である。
第1章でも述べたが、3D空間においても点は位置ベクトルというベクトルとして扱うことができる。したがって、点 $P$ にベクトル $\boldsymbol{\mathsf{v}}$ を加算することは詳しく言えば、位置ベクトル $P$ に方向を表すベクトル $\boldsymbol{\mathsf{v}}$ を加算することを意味し、この演算はベクトル同士の加算として以下のように計算される。
点 $P = (x, y, z)$ にベクトル $\boldsymbol{\mathsf{v}} = (a, b, c)$ を加算
\[P + \boldsymbol{\mathsf{v}} = \begin{pmatrix}x \\y \\z \end{pmatrix}+\begin{pmatrix}a \\b \\c \end{pmatrix} =\begin{pmatrix}x + a \\y + b \\z + c\end{pmatrix} \]
(例1) $P = (2, 1, -2)$ (図1)をベクトル $\boldsymbol{\mathsf{v}} = (7, 3, 5)$ (図2)だけ移動させる。
図3からわかるようにベクトルによる平行移動は、ベクトル $\boldsymbol{\mathsf{v}}$ の始点を点 $P$ の移動前の位置に置いたとき、そのときのベクトル $\boldsymbol{\mathsf{v}}$ の終点が点 $P$ の移動後の位置になる。
(例2) 点 $P = (1, 2, -3)$ (図4)をベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ (図5)だけ移動させる。
(例3) ある点 $P$ を上の例2のベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ (図5)によって移動させたところ、下図7で示される位置 $P = (2, 4, 0)$ に移動した。移動前の位置を $P = (a, b, c)$ として各値を求めてみよう。
移動前の位置が $P = (a, b, c)$ で、これにベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を加算した結果 $(2, 4, 0)$ へ移動したから、これを計算で表すと以下のようになる(以下では赤い $\color{red}P$ が移動後の $P$ を表し、青い $\color{blue}P$ が移動前の $P$ を表している)。
\[\color{blue}P + \boldsymbol{\mathsf{v}} = \begin{pmatrix}a \\b \\c \end{pmatrix} +\begin{pmatrix}3 \\4 \\-1 \end{pmatrix} =\begin{pmatrix}2 \\4 \\0 \end{pmatrix} = \color{red}P \] したがって点 $P$ の移動前の位置 $(a, b, c)$ は次のように求められる。\[\color{blue}P =\begin{pmatrix}a \\b \\c \end{pmatrix} =\begin{pmatrix}2 \\4 \\0 \end{pmatrix} -\begin{pmatrix}3 \\4 \\-1 \end{pmatrix} = \color{red}P - \boldsymbol{\mathsf{v}}\] この式が意味することは、(移動前の点 $P$ を求めるには)移動後の点 $P = (2, 4, 0)$ からベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を減算するということである。ベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を減算することは、ベクトル $\boldsymbol{\mathsf{v}}$ の向きを反転させたベクトル $-\boldsymbol{\mathsf{v}} = -(3, 4, -1) = (-3, -4, 1)$ を加算することに等しいから、結局上の式は、\[\color{blue}P = \color{red}P - \boldsymbol{\mathsf{v}} = \color{red}P + (-\boldsymbol{\mathsf{v}})=\begin{pmatrix}2 \\4 \\0 \end{pmatrix} +\begin{pmatrix}-3 \\-4 \\1 \end{pmatrix} =\begin{pmatrix}-1 \\0 \\1 \end{pmatrix} \] となり、移動前の点 $P$ の位置は $P = (-1, 0, 1)$ であることがわかる。
以上の過程を図7～9に示す。
3D空間では、任意のベクトルを正規化して単位ベクトルにすると、その単位ベクトルの始点が原点にあるものとすれば終点は半径 $1$ の球面上のいずれかの位置を指している。
図10にベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、図11にそれらを正規化した単位ベクトル $\boldsymbol{u_1}$、$\boldsymbol{u_2}$ を示す($\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$ はいずれも始点は原点である。また、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の終点は半径 $1$ の球面上を指している)。
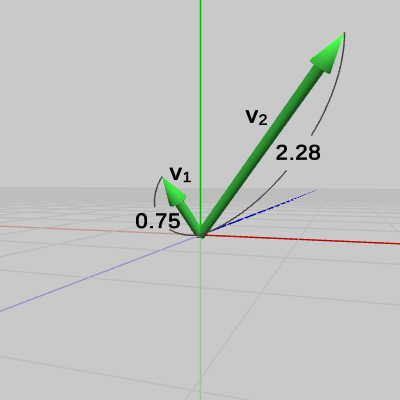
図10 ベクトルv1、v2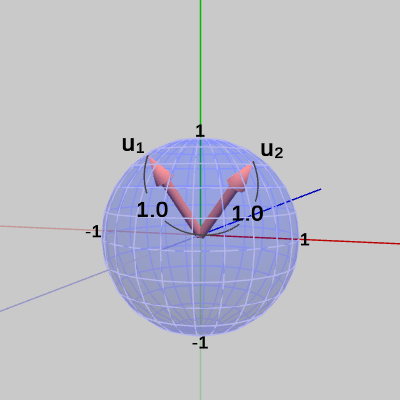 
図11 単位ベクトルu1、u2 (単位ベクトルの終点は半径1の球面上に位置する)
単位ベクトル $\boldsymbol{u_1}$ は、ベクトル $\boldsymbol{\mathsf{v_1}}$ を $\boldsymbol{\mathsf{v_1}}$ の方向に伸ばして大きさを $1$ にしたものである。
単位ベクトル $\boldsymbol{u_2}$ は、ベクトル $\boldsymbol{\mathsf{v_2}}$ を $\boldsymbol{\mathsf{v_2}}$ の方向に縮めて大きさを $1$ にしたものである。
$\boldsymbol{u_1}$ と $\boldsymbol{\mathsf{v_1}}$、そして $\boldsymbol{u_2}$ と $\boldsymbol{\mathsf{v_2}}$ は大きさは異なるが方向は同じである。
(これ以降の文章中においては、スペース上の問題で数式内でもベクトルが横並びの行ベクトルで記述されていることに注意してほしい)
単位ベクトルは、ベクトルの各成分をベクトルの大きさで割ることで求められる。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y, z)$ の正規化 ($\boldsymbol{\mathsf{v}}$ の大きさを $|\boldsymbol{\mathsf{v}}|$ とする)
実際に大きさが $1$ であることを確認しよう。
(例4) 点 $Q = (-5, 3, 2)$ (図12)をベクトル $\boldsymbol{w} = (4, 4, -3)$ (図13)の方向へ $6$ だけ移動させる。
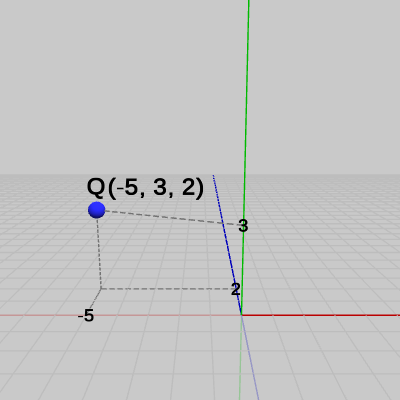
図12 点Q = (-5, 3, 2)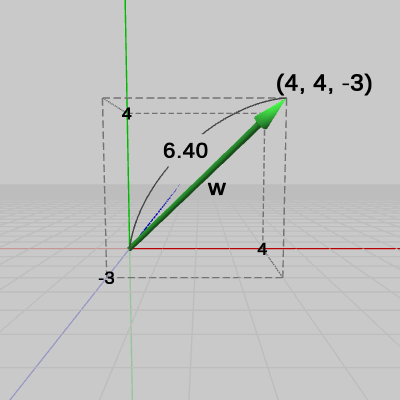 
図13 ベクトルw = (4, 4, -3)
ここでは移動する距離が $6$ と指定されているが、ベクトル $\boldsymbol{w}$ の大きさは $6$ ではないので $\boldsymbol{w}$ をそのまま加算するだけでは正しい移動にはならない。そこで、ベクトル $\boldsymbol{w}$ の単位ベクトルを使って以下のように解決する。
ベクトル $\boldsymbol{w}$ の単位ベクトルを $\boldsymbol{u}$ とすると、単位ベクトル $\boldsymbol{u}$ はベクトル $\boldsymbol{w}$ と方向は同じで、大きさが $1$ のベクトルである。3-1節で見たようにベクトルの各成分を $s$ 倍すると、そのベクトルの大きさも $s$ 倍になる。したがって、単位ベクトル $\boldsymbol{u}$ を $6$ 倍したベクトルを $\boldsymbol{6u}$ とすれば、$\boldsymbol{6u}$ はベクトル $\boldsymbol{w}$ と方向は同じで大きさが $6$ のベクトルであるから、この $\boldsymbol{6u}$ を点 $Q$ に加算すれば $Q$ の正しい移動後の位置が求められるわけである。
まず、ベクトル $\boldsymbol{w}$ の単位ベクトル $\boldsymbol{u}$ をもとめる。\begin{align*}&|\boldsymbol{w}| = \sqrt{4^2 + 4^2 + (-3)^2} = \sqrt{41} \\&\boldsymbol{u}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}=\left(\frac{4}{|\boldsymbol{w}|}, \frac{4}{|\boldsymbol{w}|}, \frac{-3}{|\boldsymbol{w}|}\right) =\left(\frac{4}{\sqrt{41}}, \frac{4}{\sqrt{41}}, \frac{-3}{\sqrt{41}}\right) \end{align*}そして、点 $Q$ に単位ベクトル $\boldsymbol{u}$ を $6$ 倍したベクトル $\boldsymbol{6u}$ を加算する。
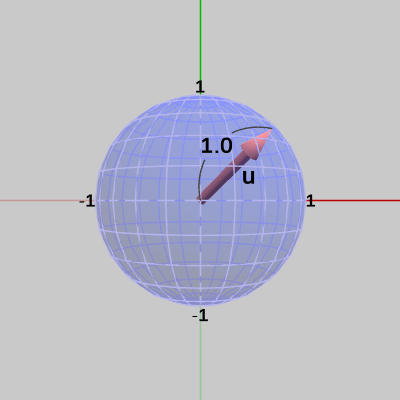
図14 ベクトルwを正規化した単位ベクトルu(方向はwと同じ向き)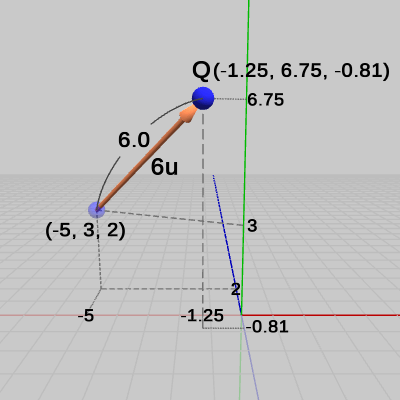 
図15 点Qに単位ベクトルuを6倍した6uを加算
(例5) 図16に示される位置に点 $Q = (-2, 2, 1)$、点 $R = (5, 3, -1)$ が置かれている($QR$ 間の距離は約 $7.35$)。線分 $QR$ の $R$ 側の延長上に $R$ を動かして、2点間の距離を $10$ にする問題について考えよう。
手順は次の通り。
(1) $Q$ を始点、$R$ を終点とするベクトルを $\boldsymbol{w}$ とする。\begin{align*}\boldsymbol{w} &= R - Q = (5,\ 3, -1) - (-2,\ 2,\ 1)= (7,\ 1, -2) \\|\boldsymbol{w}| &= \sqrt{7^2 + 1^2 + (-2)^2} = \sqrt{54} \risingdotseq 7.35\end{align*}(2) $\boldsymbol{w}$ の単位ベクトルを $\boldsymbol{u}$ とし、$\boldsymbol{u}$ を求める。
\[\boldsymbol{u}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}=\left(\frac{7}{|\boldsymbol{w}|}, \frac{1}{|\boldsymbol{w}|}, \frac{-2}{|\boldsymbol{w}|}\right) =\left(\frac{7}{\sqrt{54}}, \frac{1}{\sqrt{54}}, \frac{-2}{\sqrt{54}}\right) \](3) 単位ベクトル $\boldsymbol{u}$ を $10$ 倍したベクトル $10\boldsymbol{u}$ を $Q$ に加算する(この位置に $R$ を移動させる)。
手順(1)はすでに図17に示されているので、手順(2)、(3)を以下の図に示す。
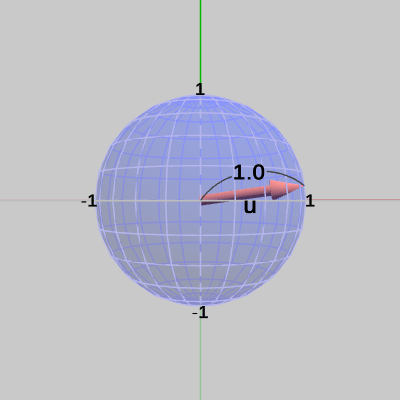
図19 ベクトルwを正規化した単位ベクトルu(方向はwと同じ向き)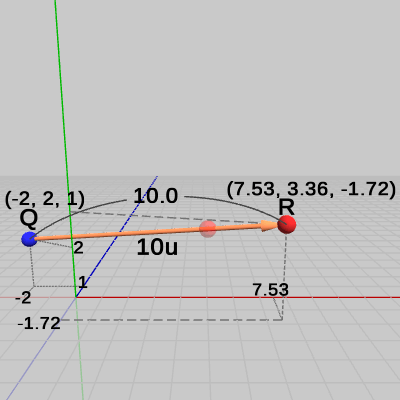 
図20 Q + 10u の位置にRを移動
単位ベクトル $\boldsymbol{u}$ を $10$ 倍したベクトル $10\boldsymbol{u}$ は、ベクトル $\boldsymbol{w}$ と方向は同じで大きさが $10$ のベクトルであるから、$Q + 10u$ で示される位置は $Q$ から $\boldsymbol{w}$ の方向に $10$ だけ離れた位置ということになる(図20における半透明の赤い点は $R$ の移動前の位置)。
最後に、本節で述べた内容に関してのプログラムを作成する。
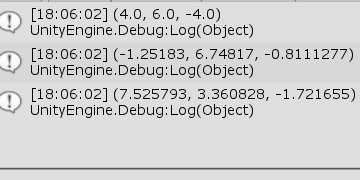
図21 Code1 実行結果 最初の計算は、本節の(例2)で行われたものであり、点 $P=(2,1,−2)$ をベクトル $\boldsymbol{\mathsf{v}}=(3,4,-1)$ だけ移動させたときの位置を求めている。
次の計算は(例4)で行われたものであり、点 $Q=(−5,3,2)$ をベクトル $\boldsymbol{\mathsf{w}}=(4,4,−3)$ の方向へ $6$ だけ移動させたときの位置を求めている (プログラムでいえばQとQ1の距離が $6$ になる)。10行目の normalized はVector3構造体のプロパティで、そのベクトルの単位ベクトルを表すものである。すなわち、w.normalized はベクトル $\boldsymbol{\mathsf{w}}$ の単位ベクトルを意味している。
最後の計算は(例5)で行われたものであり、点 $Q=(−2,2,1)$、点 $R = (5, 3, -1)$ 間の距離を、線分 $QR$ の $R$ 側の延長上に $R$ を動かして $10$ にするという計算である (プログラムでいえばQとR1の距離が $10$ になる)。
実行結果(図21)に示されるように、いずれの結果も上での計算結果と(小数第3位を四捨五入すれば)一致する。
第1章でも述べたが、3D空間においても点は位置ベクトルというベクトルとして扱うことができる。したがって、点 $P$ にベクトル $\boldsymbol{\mathsf{v}}$ を加算することは詳しく言えば、位置ベクトル $P$ に方向を表すベクトル $\boldsymbol{\mathsf{v}}$ を加算することを意味し、この演算はベクトル同士の加算として以下のように計算される。
点 $P = (x, y, z)$ にベクトル $\boldsymbol{\mathsf{v}} = (a, b, c)$ を加算
\[P + \boldsymbol{\mathsf{v}} = \begin{pmatrix}x \\y \\z \end{pmatrix}+\begin{pmatrix}a \\b \\c \end{pmatrix} =\begin{pmatrix}x + a \\y + b \\z + c\end{pmatrix} \]
A) 単純な加算による平行移動
まず始めに、点にベクトルをそのまま加算するだけの例をいくつか見ていこう。(例1) $P = (2, 1, -2)$ (図1)をベクトル $\boldsymbol{\mathsf{v}} = (7, 3, 5)$ (図2)だけ移動させる。
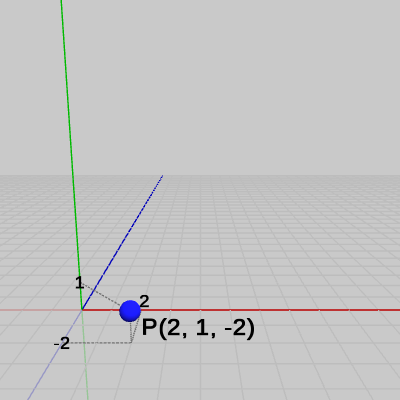図1 点P = (2, 1, -2)
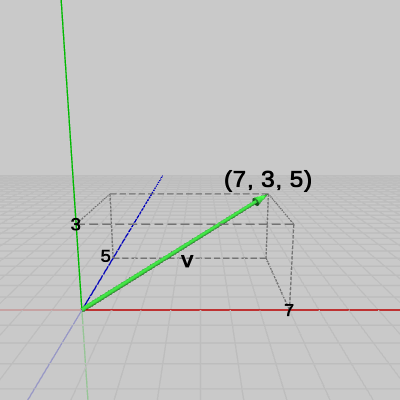図2 ベクトルv = (7, 3, 5)
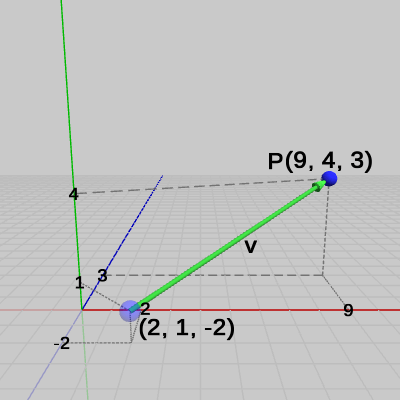図3 P + v = (9, 4, 3)
図3からわかるようにベクトルによる平行移動は、ベクトル $\boldsymbol{\mathsf{v}}$ の始点を点 $P$ の移動前の位置に置いたとき、そのときのベクトル $\boldsymbol{\mathsf{v}}$ の終点が点 $P$ の移動後の位置になる。
(例2) 点 $P = (1, 2, -3)$ (図4)をベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ (図5)だけ移動させる。
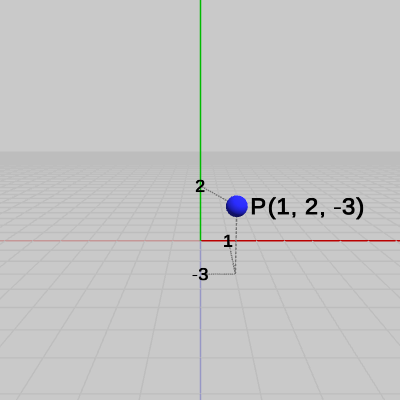図4 点P = (1, 2, -3)
図5 ベクトルv = (3, 4, -1)
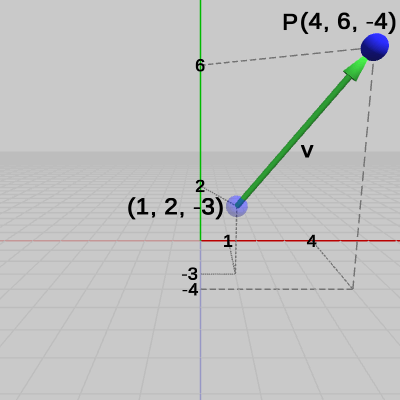図6 P + v = (4, 6, -4)
(例3) ある点 $P$ を上の例2のベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ (図5)によって移動させたところ、下図7で示される位置 $P = (2, 4, 0)$ に移動した。移動前の位置を $P = (a, b, c)$ として各値を求めてみよう。
移動前の位置が $P = (a, b, c)$ で、これにベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を加算した結果 $(2, 4, 0)$ へ移動したから、これを計算で表すと以下のようになる(以下では赤い $\color{red}P$ が移動後の $P$ を表し、青い $\color{blue}P$ が移動前の $P$ を表している)。
\[\color{blue}P + \boldsymbol{\mathsf{v}} = \begin{pmatrix}a \\b \\c \end{pmatrix} +\begin{pmatrix}3 \\4 \\-1 \end{pmatrix} =\begin{pmatrix}2 \\4 \\0 \end{pmatrix} = \color{red}P \] したがって点 $P$ の移動前の位置 $(a, b, c)$ は次のように求められる。\[\color{blue}P =\begin{pmatrix}a \\b \\c \end{pmatrix} =\begin{pmatrix}2 \\4 \\0 \end{pmatrix} -\begin{pmatrix}3 \\4 \\-1 \end{pmatrix} = \color{red}P - \boldsymbol{\mathsf{v}}\] この式が意味することは、(移動前の点 $P$ を求めるには)移動後の点 $P = (2, 4, 0)$ からベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を減算するということである。ベクトル $\boldsymbol{\mathsf{v}} = (3, 4, -1)$ を減算することは、ベクトル $\boldsymbol{\mathsf{v}}$ の向きを反転させたベクトル $-\boldsymbol{\mathsf{v}} = -(3, 4, -1) = (-3, -4, 1)$ を加算することに等しいから、結局上の式は、\[\color{blue}P = \color{red}P - \boldsymbol{\mathsf{v}} = \color{red}P + (-\boldsymbol{\mathsf{v}})=\begin{pmatrix}2 \\4 \\0 \end{pmatrix} +\begin{pmatrix}-3 \\-4 \\1 \end{pmatrix} =\begin{pmatrix}-1 \\0 \\1 \end{pmatrix} \] となり、移動前の点 $P$ の位置は $P = (-1, 0, 1)$ であることがわかる。
以上の過程を図7～9に示す。
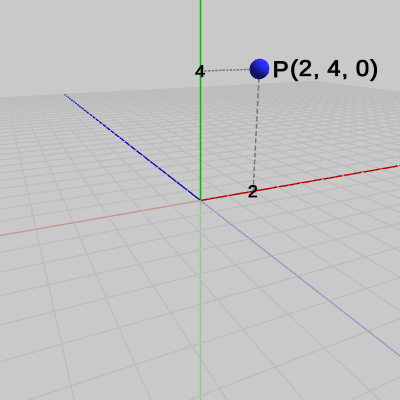図7 移動後の点P = (2, 4, 0)
図8 ベクトルvとその向きを反転させたベクトル -v = (-3, -4, 1)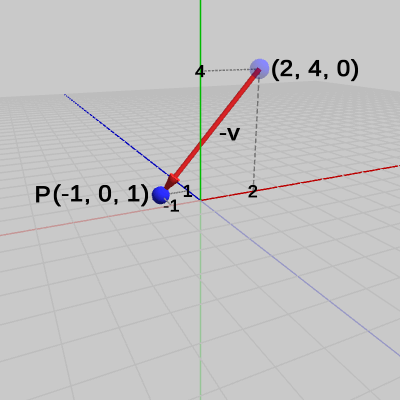
図9 移動前の点P = (-1, 0, 1)
B) 単位ベクトル
2D空間の場合と同じく、3D空間においてもベクトルの大きさを $1$ にすることを正規化(Normalization)といい、大きさが $1$ のベクトルのことを単位ベクトル(Unit Vector)という。3D空間では、任意のベクトルを正規化して単位ベクトルにすると、その単位ベクトルの始点が原点にあるものとすれば終点は半径 $1$ の球面上のいずれかの位置を指している。
図10にベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、図11にそれらを正規化した単位ベクトル $\boldsymbol{u_1}$、$\boldsymbol{u_2}$ を示す($\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$ はいずれも始点は原点である。また、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の終点は半径 $1$ の球面上を指している)。
単位ベクトル $\boldsymbol{u_1}$ は、ベクトル $\boldsymbol{\mathsf{v_1}}$ を $\boldsymbol{\mathsf{v_1}}$ の方向に伸ばして大きさを $1$ にしたものである。
単位ベクトル $\boldsymbol{u_2}$ は、ベクトル $\boldsymbol{\mathsf{v_2}}$ を $\boldsymbol{\mathsf{v_2}}$ の方向に縮めて大きさを $1$ にしたものである。
$\boldsymbol{u_1}$ と $\boldsymbol{\mathsf{v_1}}$、そして $\boldsymbol{u_2}$ と $\boldsymbol{\mathsf{v_2}}$ は大きさは異なるが方向は同じである。
(これ以降の文章中においては、スペース上の問題で数式内でもベクトルが横並びの行ベクトルで記述されていることに注意してほしい)
単位ベクトルは、ベクトルの各成分をベクトルの大きさで割ることで求められる。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y, z)$ の正規化 ($\boldsymbol{\mathsf{v}}$ の大きさを $|\boldsymbol{\mathsf{v}}|$ とする)
\[\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}=\left(\frac{x}{|\boldsymbol{\mathsf{v}}|}, \frac{y}{|\boldsymbol{\mathsf{v}}|}, \frac{z}{|\boldsymbol{\mathsf{v}}|}\right) =\left(\frac{x}{\sqrt{x^2 + y^2 + z^2}}, \frac{y}{\sqrt{x^2 + y^2 + z^2}}, \frac{z}{\sqrt{x^2 + y^2 + z^2}}\right) \]
実際に大きさが $1$ であることを確認しよう。
\begin{align*}\left|\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}\right|& =\sqrt{\left(\frac{x}{\sqrt{x^2 + y^2 + z^2}}\right)^2 + \left(\frac{y}{\sqrt{x^2 + y^2 + z^2}}\right)^2 + \left(\frac{z}{\sqrt{x^2 + y^2 + z^2}}\right)^2} \\\\& = \sqrt{\frac{x^2}{\left(\sqrt{x^2 + y^2 + z^2}\right)^2} + \frac{y^2}{\left(\sqrt{x^2 + y^2 + z^2}\right)^2} + \frac{z^2}{\left(\sqrt{x^2 + y^2 + z^2}\right)^2}} \\\\& = \sqrt{\frac{x^2 + y^2 + z^2}{\left(\sqrt{x^2 + y^2 + z^2}\right)^2}} = \sqrt{\frac{x^2 + y^2 + z^2}{x^2 + y^2 + z^2}} = 1\end{align*}
C) 単位ベクトルを使った平行移動
以下の例では、指定方向に指定された距離だけ点を移動させる問題を扱う。(例4) 点 $Q = (-5, 3, 2)$ (図12)をベクトル $\boldsymbol{w} = (4, 4, -3)$ (図13)の方向へ $6$ だけ移動させる。
ここでは移動する距離が $6$ と指定されているが、ベクトル $\boldsymbol{w}$ の大きさは $6$ ではないので $\boldsymbol{w}$ をそのまま加算するだけでは正しい移動にはならない。そこで、ベクトル $\boldsymbol{w}$ の単位ベクトルを使って以下のように解決する。
ベクトル $\boldsymbol{w}$ の単位ベクトルを $\boldsymbol{u}$ とすると、単位ベクトル $\boldsymbol{u}$ はベクトル $\boldsymbol{w}$ と方向は同じで、大きさが $1$ のベクトルである。3-1節で見たようにベクトルの各成分を $s$ 倍すると、そのベクトルの大きさも $s$ 倍になる。したがって、単位ベクトル $\boldsymbol{u}$ を $6$ 倍したベクトルを $\boldsymbol{6u}$ とすれば、$\boldsymbol{6u}$ はベクトル $\boldsymbol{w}$ と方向は同じで大きさが $6$ のベクトルであるから、この $\boldsymbol{6u}$ を点 $Q$ に加算すれば $Q$ の正しい移動後の位置が求められるわけである。
まず、ベクトル $\boldsymbol{w}$ の単位ベクトル $\boldsymbol{u}$ をもとめる。\begin{align*}&|\boldsymbol{w}| = \sqrt{4^2 + 4^2 + (-3)^2} = \sqrt{41} \\&\boldsymbol{u}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}=\left(\frac{4}{|\boldsymbol{w}|}, \frac{4}{|\boldsymbol{w}|}, \frac{-3}{|\boldsymbol{w}|}\right) =\left(\frac{4}{\sqrt{41}}, \frac{4}{\sqrt{41}}, \frac{-3}{\sqrt{41}}\right) \end{align*}そして、点 $Q$ に単位ベクトル $\boldsymbol{u}$ を $6$ 倍したベクトル $\boldsymbol{6u}$ を加算する。
\begin{align*}Q + 6\boldsymbol{u} &= (-5,\ 3,\ 2) + 6\left(\frac{4}{\sqrt{41}}, \frac{4}{\sqrt{41}}, \frac{-3}{\sqrt{41}}\right) \\&=(-5,\ 3,\ 2) + \left(\frac{24}{\sqrt{41}}, \frac{24}{\sqrt{41}}, \frac{-18}{\sqrt{41}}\right) \\&\risingdotseq(-5,\ 3,\ 2) + (3.75,\ 3.75, -2.81) \\&= (-1.25,\ 6.75, -0.81)\end{align*}
以上の手順を図14、図15に示す。 (例5) 図16に示される位置に点 $Q = (-2, 2, 1)$、点 $R = (5, 3, -1)$ が置かれている($QR$ 間の距離は約 $7.35$)。線分 $QR$ の $R$ 側の延長上に $R$ を動かして、2点間の距離を $10$ にする問題について考えよう。
図16 Q = (-2, 2, 1)、R = (5, 3, -1)
図17 ベクトル w = R - Q = (7, 1, -2) (w の大きさはQR間の距離に等しく、約7.35である)
図18 ベクトル w = (7, 1, -2)の始点を原点に移動
手順は次の通り。
(1) $Q$ を始点、$R$ を終点とするベクトルを $\boldsymbol{w}$ とする。\begin{align*}\boldsymbol{w} &= R - Q = (5,\ 3, -1) - (-2,\ 2,\ 1)= (7,\ 1, -2) \\|\boldsymbol{w}| &= \sqrt{7^2 + 1^2 + (-2)^2} = \sqrt{54} \risingdotseq 7.35\end{align*}(2) $\boldsymbol{w}$ の単位ベクトルを $\boldsymbol{u}$ とし、$\boldsymbol{u}$ を求める。
\[\boldsymbol{u}=\frac{\boldsymbol{w}}{|\boldsymbol{w}|}=\left(\frac{7}{|\boldsymbol{w}|}, \frac{1}{|\boldsymbol{w}|}, \frac{-2}{|\boldsymbol{w}|}\right) =\left(\frac{7}{\sqrt{54}}, \frac{1}{\sqrt{54}}, \frac{-2}{\sqrt{54}}\right) \](3) 単位ベクトル $\boldsymbol{u}$ を $10$ 倍したベクトル $10\boldsymbol{u}$ を $Q$ に加算する(この位置に $R$ を移動させる)。
\begin{align*}Q + 10\boldsymbol{u} &=(-2,\ 2,\ 1) + 10\left(\frac{7}{\sqrt{54}}, \frac{1}{\sqrt{54}}, \frac{-2}{\sqrt{54}}\right) \\&= (-2,\ 2,\ 1) + \left(\frac{70}{\sqrt{54}}, \frac{10}{\sqrt{54}}, \frac{-20}{\sqrt{54}}\right) \\&\risingdotseq(-2,\ 2,\ 1) + (9.53,\ 1.36, -2.72) \\&=(7.53,\ 3.36, -1.72)\end{align*}
手順(1)はすでに図17に示されているので、手順(2)、(3)を以下の図に示す。
単位ベクトル $\boldsymbol{u}$ を $10$ 倍したベクトル $10\boldsymbol{u}$ は、ベクトル $\boldsymbol{w}$ と方向は同じで大きさが $10$ のベクトルであるから、$Q + 10u$ で示される位置は $Q$ から $\boldsymbol{w}$ の方向に $10$ だけ離れた位置ということになる(図20における半透明の赤い点は $R$ の移動前の位置)。
最後に、本節で述べた内容に関してのプログラムを作成する。
# Code1
[Code1] (実行結果 図21)
// (例2)
Vector3 P = new Vector3(1, 2, -3);
Vector3 v = new Vector3(3, 4, -1);
Vector3 P1 = P + v;
Debug.Log(P1);
// (例4)
Vector3 Q = new Vector3(-5, 3, 2);
Vector3 w = new Vector3(4, 4, -3);
Vector3 Q1 = Q + 6.0f * w.normalized;
Debug.Log("(" + Q1.x + ", " + Q1.y + ", " + Q1.z + ")");
// (例5)
Q = new Vector3(-2, 2, 1);
Vector3 R = new Vector3(5, 3, -1);
w = R - Q;
Vector3 R1 = Q + 10.0f * w.normalized;
Debug.Log("(" + R1.x + ", " + R1.y + ", " + R1.z + ")");
次の計算は(例4)で行われたものであり、点 $Q=(−5,3,2)$ をベクトル $\boldsymbol{\mathsf{w}}=(4,4,−3)$ の方向へ $6$ だけ移動させたときの位置を求めている (プログラムでいえばQとQ1の距離が $6$ になる)。10行目の normalized はVector3構造体のプロパティで、そのベクトルの単位ベクトルを表すものである。すなわち、w.normalized はベクトル $\boldsymbol{\mathsf{w}}$ の単位ベクトルを意味している。
最後の計算は(例5)で行われたものであり、点 $Q=(−2,2,1)$、点 $R = (5, 3, -1)$ 間の距離を、線分 $QR$ の $R$ 側の延長上に $R$ を動かして $10$ にするという計算である (プログラムでいえばQとR1の距離が $10$ になる)。
実行結果(図21)に示されるように、いずれの結果も上での計算結果と(小数第3位を四捨五入すれば)一致する。
© 2020-2024 Redpoll's 60 (All rights reserved)