Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-4
第3章 3D空間の基礎
$§$3-4 ベクトルの内積
ベクトルの内積は 2D空間の章では 2-20節、2-21節の衝突判定において使われたが、これ以降の3D空間の章においてもベクトルの内積は頻繁に使用される。本節では3D版の内積の基礎及び、いくつかの使用例について見ていくが、その内容は2D版の内積の復習のようなものである。
ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$の内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2\]
(計算例)
ベクトル$\boldsymbol{\mathsf{v_1}} = (1, 2, 3)$と $\boldsymbol{\mathsf{v_2}} = (6, 5, 4)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 1\cdot6 + 2\cdot5 + 3\cdot4 = 6 + 10 + 12 = 28\] ベクトル$\boldsymbol{\mathsf{v_1}} = (3, -1, -5)$と $\boldsymbol{\mathsf{v_2}} = (0,\ 5, -1)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 3\cdot0 + (-1)\cdot5 + (-5)\cdot(-1) = 0 + (-5) + 5 = 0\]
定義から明らかなように、内積は以下のように積の順序について交換可能である。
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = \boldsymbol{\mathsf{v_2}}\cdot\boldsymbol{\mathsf{v_1}}\]
また、同じベクトル同士の内積、例えばベクトル$\boldsymbol{\mathsf{v}} = (x, y, z)$同士の内積は、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = xx + yy + zz = x^2 + y^2 + z^2\] となるが、これはベクトル$\boldsymbol{\mathsf{v}}$の大きさ($|\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}$)の$2$乗に等しい。すなわち、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = |\boldsymbol{\mathsf{v}}|^2\] である。
ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$のなす角を $A$とし、$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の大きさを$|\boldsymbol{\mathsf{v_1}}|$、$|\boldsymbol{\mathsf{v_2}}|$とすれば
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2 = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\cos{A}\] である。
図1のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$は、両者のなす角が $A$である。図2は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である(両者のなす角は変わらない)。
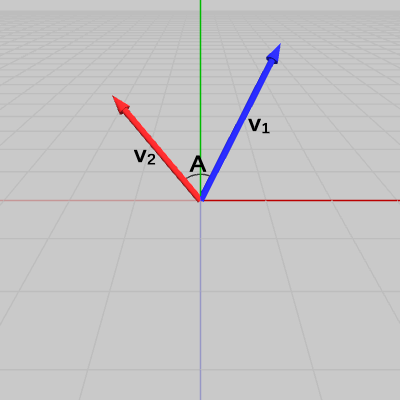
図1 ベクトルv1、v2 (両者のなす角はA)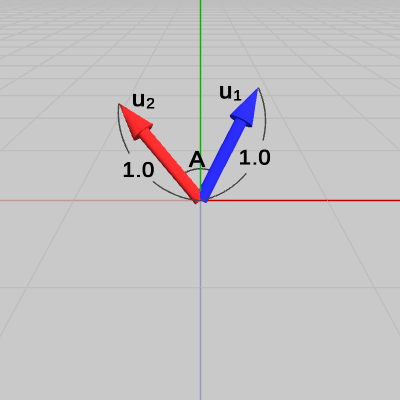 
図2 ベクトルv1、v2を正規化したu1、u2
上の等式における$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の代わりに単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$を式に使った場合、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = |\boldsymbol{u_1}||\boldsymbol{u_2}|\cos{A} \] となるが、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$は単位ベクトルであるから、$|\boldsymbol{u_1}|$、$|\boldsymbol{u_2}|$の値は$1$である。すなわち、\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} \] が成り立つ。
この結果は、2つのベクトルの単位ベクトルの内積を求めれば、その2つのベクトルのなす角を知ることが可能であることを意味している。
以下では、その特殊な例として2つのベクトルが直交している場合、あるいは平行である場合の判定方法について見ていく。
(注) 以下の例ではベクトルのなす角は、0°～180°の範囲にあるものとする。
(例1) 2つのベクトルが直交しているかどうかの判定(なす角が$90$°)
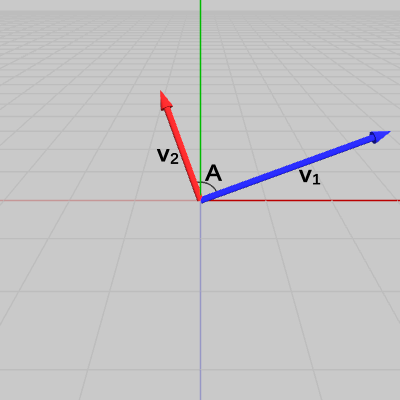
図3 ベクトルv1、v2 (両者のなす角はA)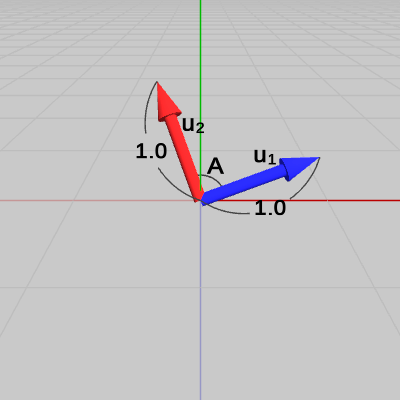 
図4 ベクトルv1、v2を正規化したu1、u2
図3に示されるベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$のなす角を $A$とする。図4は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0\] 上で述べたように、単位ベクトルの内積はそれらのなす角の余弦($\cos$)に等しいから、結局\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 0\] となる。
$\cos{A} = 0$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 90$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$0$になる場合では、両者は直交していることがわかる(2つのベクトルが直交している場合は、両者を正規化せずに内積を計算しても結果は$0$になる。つまり、この例では$\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$の値も$0$である)。
(例2) 2つのベクトルが平行であるかどうかの判定 1 (なす角が$0$°)
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図5に示される位置に置かれている。この2つのベクトルのなす角は、両者の始点を原点に移動させたときの2つのベクトルのなす角のことである。今回の例では、2つのベクトルを原点に移動させたときに(図6)、2つのベクトルが重なってしまっているので角度の表示がされていないが、ここでも両者のなす角を$A$とする。
図7は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1\] 先程と同じように、両者のなす角の余弦($\cos$)を使って表せば、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 1\] となる。
$\cos{A} = 1$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 0$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$1$になる場合では、両者は平行でありベクトルの向きも同じであることがわかる。
(例3) 2つのベクトルが平行であるかどうかの判定 2 (なす角が$180$°)
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図8に示される位置に置かれている。この2つのベクトルのなす角は、上の例で述べたように両者の始点を原点に移動させたときの2つのベクトルのなす角のことであり、図9に示されるようにここでも両者のなす角を$A$とする。
図10は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = -1\] $\cos{A} = -1$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 180$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$-1$になる場合では、両者は平行であるがベクトルの向きは逆向きであることがわかる。
以上をまとめると、2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ 及び、それらの単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積について次のことがいえる。
(ⅰ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0$ のとき、2つのベクトルは直交する。
(ⅱ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1$ のとき、2つのベクトルは平行であり同じ向きである。
(ⅲ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = -1$ のとき、2つのベクトルは平行であり逆向きである。
ここではベクトルのなす角の範囲を$0$°～$180$°の範囲に制限したが、この範囲を$0$°より下、あるいは$180$°より上の範囲に広げても上記の(ⅰ)～(ⅲ)は成立する。
図11 点Pと直線m 
図12 点Pから直線mへの垂線と交点Q
(以下では原点を$O$で表す。)
原点$O$を始点、点$P$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とする。また、直線$m$の方向(原点$O$から点$Q$へ向かう方向)を表す単位ベクトルを$\boldsymbol{u}$とし、その始点を原点に置く。ベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$のなす角を $A$とする(以上は図13参照)。
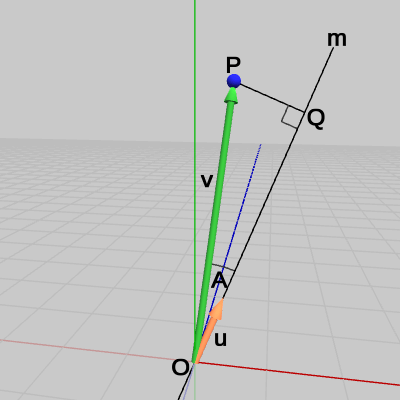
図13 ベクトルvと単位ベクトルu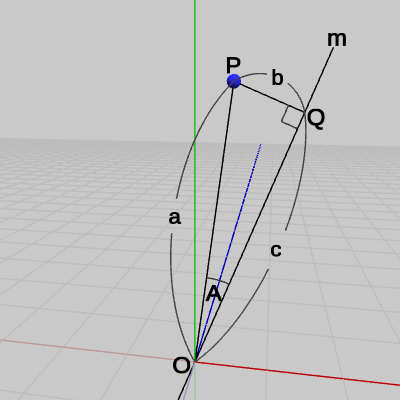 
図14 三角形OPQの各辺の長さa、b、c (c = |v|cosA)
ここでベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$の内積を計算すると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}||\boldsymbol{u}|\cos{A} = |\boldsymbol{\mathsf{v}}|\cos{A}\] であるが、この $|\boldsymbol{\mathsf{v}}|\cos{A}$ が何を表すかについて図14を用いて説明しよう。
図14では原点$O$と点$P$、$Q$を結んだ三角形(直角三角形)の各辺に記号がふられてある。これは各辺の長さを表し、すなわち辺$OP$の長さが$a$、辺$PQ$の長さが$b$、辺$OQ$の長さが$c$である。ベクトル$\boldsymbol{\mathsf{v}}$は、$O$と$P$を結ぶベクトルであるから、$\boldsymbol{\mathsf{v}}$の大きさ $|\boldsymbol{\mathsf{v}}|$ は辺$OP$の長さに等しい、すなわち $|\boldsymbol{\mathsf{v}}| = a$ である。
そして、$\triangle{OPQ}$は直角三角形であるから辺$OP$と辺$OQ$の長さについて次の関係が成り立つ。
\[ a\cos{A} = c \] 以上から、
\[ |\boldsymbol{\mathsf{v}}|\cos{A} = c \] つまり $|\boldsymbol{\mathsf{v}}|\cos{A}$ は辺$OQ$の長さに等しいことがわかる。原点$O$から点$Q$の方向を表す単位ベクトルは$\boldsymbol{u}$で、原点$O$から点$Q$までの長さが $|\boldsymbol{\mathsf{v}}|\cos{A}$ であるから、点$Q$の位置は
\[ Q = (|\boldsymbol{\mathsf{v}}|\cos{A})\boldsymbol{u} \] で求められる。
C)において垂線の足である点$Q$を求める過程を再度見直してみよう。
原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$と、直線$m$の方向を表す単位ベクトル$\boldsymbol{u}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}|\cos{A}$ は、原点$O$から点$Q$までの長さに等しいのであった。そして、原点から直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れた位置に、点$P$からの垂線の足である点$Q$はあるのであった。このことを便宜上、「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」という言い方で表す(つまり点$P$の直線$m$方向の距離とは、原点から(垂線の足)点$Q$までの距離である)。
以上をふまえて本題に入る。
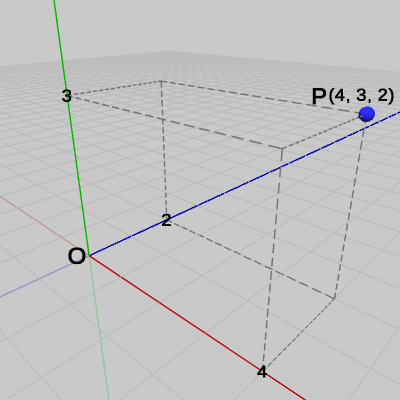
図15 点P = (4, 3, 2) 図15では点$P$が$(4, 3, 2)$の位置に置かれている。今まで特に顧みることはなかったが、点を表す座標値というものは何を意味しているのであろうか。点$P = (4, 3, 2)$とは点$P$のx座標が$4$であり、y座標が$3$、z座標が$2$であることを意味するが、「x座標が$4$」とは具体的には何のことであろうか。いささか自明に過ぎる問いであるが、ここで点の座標について幾らか丁寧な解説を試みよう。
点$P$の座標が$(4, 3, 2)$であるとは、点$P$を図16のように原点に置いてから、まず始めにx軸方向に$4$移動させ(図17)、次にy軸方向に$3$移動させ(図18)、そして最後にz軸方向に$2$移動させる(図15)、この原点からの3回の移動後の$P$の位置のことを意味している。
言い換えれば、点の座標値における各座標(x座標、y座標、z座標)は、その点が原点から各軸の方向にどれだけ離れているかを表している。点$P = (4, 3, 2)$の場合でいえば、点$P$が原点からx軸方向に$4$、y軸方向に$3$、z軸方向に$2$だけ離れていることを表している。
点$P$が原点からx軸方向、y軸方向、z軸方向にどれだけ離れているかは図15を見ればわかるが、ここでは内積を使ってその距離を計算してみよう。
そのために原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と、x軸、y軸、z軸の各方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$、$\boldsymbol{u_y} = (0, 1, 0)$、$\boldsymbol{u_z} = (0, 0, 1)$を用意する(図19、図20)。
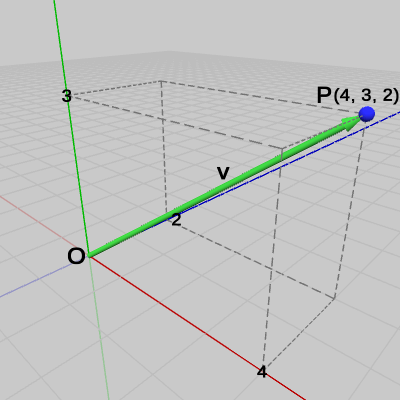
図19 ベクトルv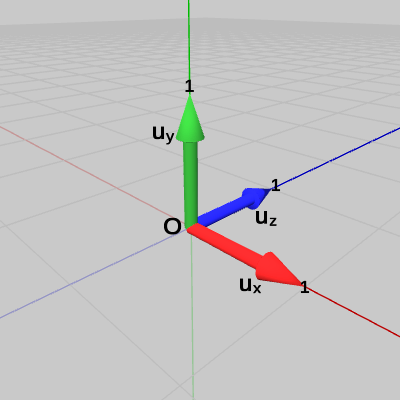 
図20 単位ベクトルux、uy、uz
まず、点$P$が原点からx軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とx軸方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_x}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} = 4\cdot1 + 3\cdot0 + 2\cdot0 = 4\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \]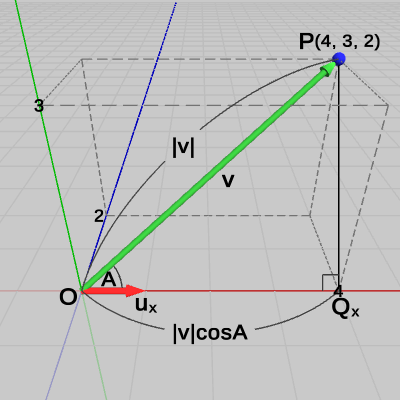 
図21 点Pのx軸方向の距離 であるが、この内積が何を表すかは C)で述べたが、再度図21を使って説明しよう。
点$P$からx軸へ垂線をおろし、その足を点$Q_x$とする($\triangle{OPQ_x}$は直角三角形になる)。C)で見たように、原点$O$から点$Q_x$までの距離は、原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$とx軸方向の単位ベクトル$\boldsymbol{u_x}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} (= |\boldsymbol{\mathsf{v}}|\cos{A})$ であるが、これは上で求めたとおり $4$ である。
先程、C)の点$P$について次のような言い方を用いた。「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」。この表現を今の例にあてはめると、直線$m$はx軸に相当し、ここでの$|\boldsymbol{\mathsf{v}}|\cos{A}$は$4$であるので、「点$P$はx軸の方向に$4$だけ離れている」という内容になる。
点$P$が原点からx軸方向にどれだけ離れているかを内積を使って求めるというのが、ここでの目的であったが、今述べてきたことがそれにあたるわけである。
点$P$のy軸方向の距離、z軸方向の距離についても同様の手順で求めることができる。
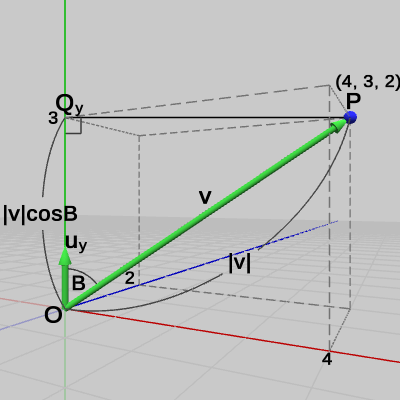
図22 点Pのy軸方向の距離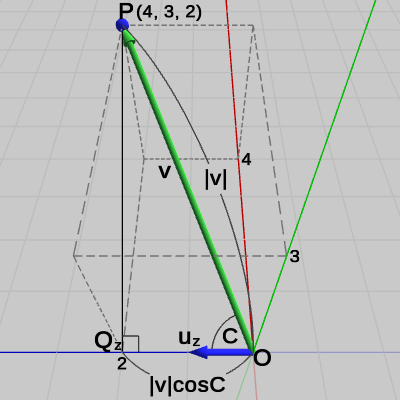 
図23 点Pのz軸方向の距離
図22に示されるようにy軸方向の距離は、点$P$からy軸におろした垂線の足を点$Q_y$とすれば、原点から$Q_y$までの距離のことである($\triangle{OPQ_y}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とy軸方向を表す単位ベクトル$\boldsymbol{u_y} = (0, 1, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_y}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_y} = 4\cdot0 + 3\cdot1 + 2\cdot0 = 3\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \] x軸の場合と同様に、この結果は「点$P$はy軸の方向に$3$だけ離れている」ことを意味している。
図23に示されるようにz軸方向の距離は、点$P$からz軸におろした垂線の足を点$Q_z$とすれば、原点から$Q_z$までの距離のことである($\triangle{OPQ_z}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とz軸方向を表す単位ベクトル$\boldsymbol{u_z} = (0, 0, 1)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_z}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_z} = 4\cdot0 + 3\cdot0 + 2\cdot1 = 2\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \] この結果は「点$P$はz軸の方向に$2$だけ離れている」ことを意味している。
だが、以上に述べてきた事柄はおそらく自明過ぎるものであろう。x軸、y軸、z軸のような基本的な座標軸上での点の位置は、そもそも点の座標値から分かることであって、わざわざ内積を使ってまで求める必要はない。確かに今まで用いてきた座標系(と座標値)ならばそれはいえる。しかし、例えばこの同じ点$P$を図24に示されるような水色、紫色、黄色の座標軸を持つ傾いた座標系を基準にした場合などでは、いささか状況が異なってくる。
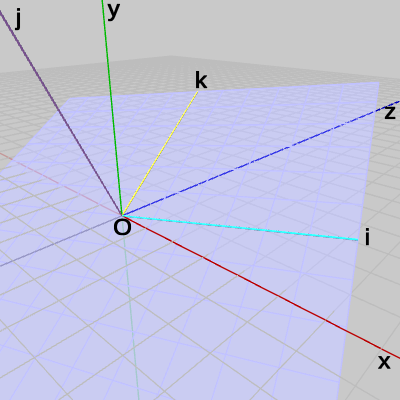
図24 ijk座標系 
図25 ijk座標系(離れた位置から)
図24に示される座標系は互いに直交する i軸(水色)、j軸(紫色)、k軸(黄色)によって構成される座標系で、便宜上ここでは ijk座標系と呼ぶことにする(図25はやや離れた位置から ijk座標系を見たもの。また、i軸、j軸、k軸についてはプラス側のみ表示してある)。そして、今まで用いてきた x軸、y軸、z軸の座標系の方をxyz座標系と呼ぶことにする。
図からわかる通り ijk座標系は傾いた座標系であり、xyz座標系とは原点が一致している。
今から問題とするのは、上で使ってきた点$P$の ijk座標系における座標値の計算である。すなわち、点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離を求めることであり、それは図26における点線の直方体の3つの辺の長さ$a$、$b$、$c$を求めることと同じである(図27は見やすくするためにxyz座標系を取り除いたもの。図における点線の図形は直方体であるので隣接する面の間の角度は直角である)。
図26 ijk座標系における点P = (a, b, c)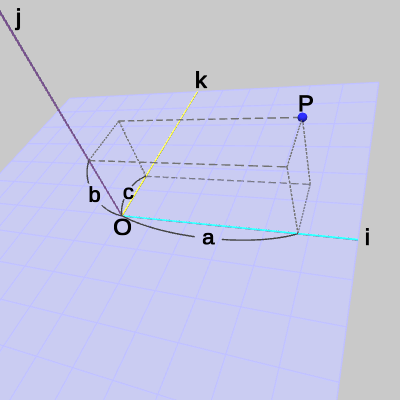 
図27 ijk座標系における点P = (a, b, c)
xyz座標系における$P$の座標は$(4, 3, 2)$であったが、ijk座標系での座標は図27を見ると、そのような整数値でないことは明らかである(もちろん点$P$の位置は今までの位置から動かしていない)。
しかし、点$P$の ijk座標系における座標を計算するのは難しいことではない。今まで見てきたことをなぞっていけば、自ずと答えが導かれる。ただし、注意すべきことが1つある。今、座標系が2つ出てきたが、この先で使用する、原点と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$、i軸、j軸、k軸の方向を表す単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$などは全てxyz座標系での値である。例えば、何度も出てきたが$(4, 3, 2)$という点$P$の座標はxyz座標系での値である。ijk座標系では図26(あるいは図27)に示されるように点$P$は$(a, b, c)$であり、$(4, 3, 2)$ではない (これは 点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離が $a$、$b$、$c$ であり $4$、$3$、$2$ ではないことを意味する)。
計算手順については今までと同様である。
まず、原点$O$から点$P$へのベクトル$\boldsymbol{\mathsf{v}}$を用意する(図28)。xyz座標系での値であるので、今までどおり、$\boldsymbol{\mathsf{v}} = (4, 3, 2)$である。また、i軸方向、j軸方向、k軸方向の単位ベクトルを$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$とする(図29。図からわかるようにこれらもxyz座標系での値であり、小数3位以下を省略してある)。
図の緑色の数値はベクトルの内容を表している。
図28 ベクトルv = (4, 3, 2)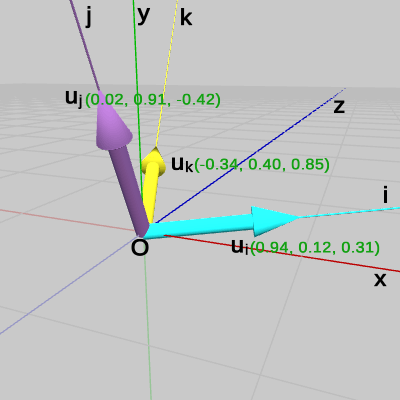 
図29 単位ベクトルui、uj、uk
(以下で使用される単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$は小数第3位以下を省略した値であるため、それらを使った計算結果もわずかな誤差を含んでいる。)
では、点$P$が原点から i軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と i軸方向を表す単位ベクトル$\boldsymbol{u_i} = (0.94, 0.12, 0.31)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_i}$のなす角を$A$とすると、
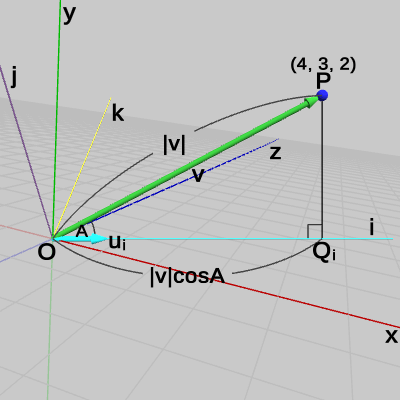
図30 点Pの i軸方向の距離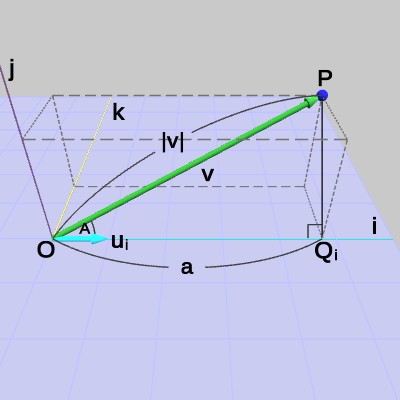 
図31 点Pの i軸方向の距離(ijk座標系のみで表示)
点$P$が原点から j軸方向にどれだけ離れているかについても同様に計算してみよう。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と j軸方向を表す単位ベクトル$\boldsymbol{u_j} = (0.02, 0.91, -0.42)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_j}$のなす角を$B$とすると、
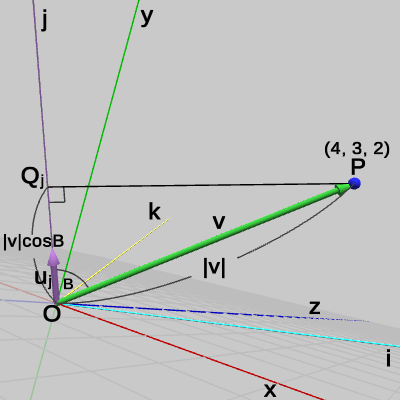
図32 点Pの j軸方向の距離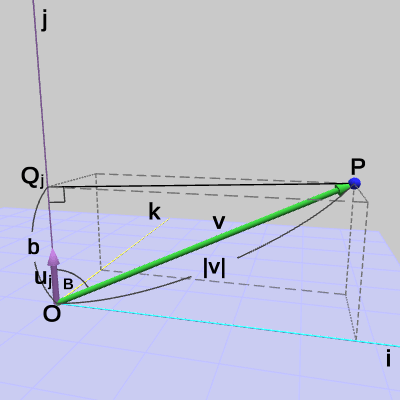 
図33 点Pの j軸方向の距離(ijk座標系のみで表示)
点$P$のk軸方向の距離についても同様の手順を繰り返せばよい。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とk軸方向を表す単位ベクトル$\boldsymbol{u_k} = (-0.34, 0.40, 0.85)$の内積は、
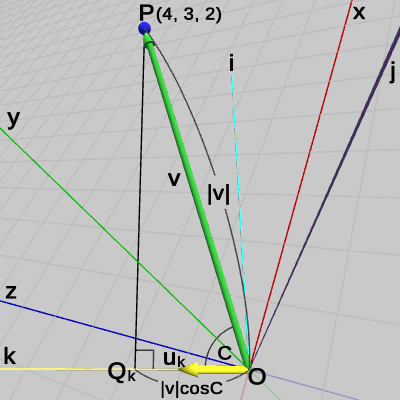
図34 点Pのk軸方向の距離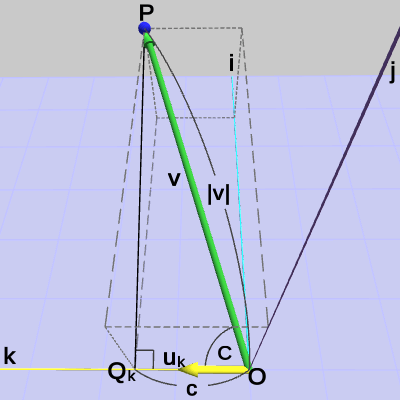 
図35 点Pのk軸方向の距離(ijk座標系のみで表示)
以上の結果をまとめると、点$P$の ijk座標系における座標(i座標、j座標、k座標)は、
\[P = (4.74,\ 1.97,\ 1.54)\]であることがわかった(図36)。
比較のために図37にxyz座標系での点$P$を示す。
また、今までの計算で使われてきた単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$の値はxyz座標系での値であったが参考のために ijk座標系での値を以下に示しておこう(図38参照。以下のカッコの中の数値は i座標、j座標、k座標の順である)。
\begin{align*}\boldsymbol{u_i} = (1, 0, 0) \\\boldsymbol{u_j} = (0, 1, 0) \\\boldsymbol{u_k} = (0, 0, 1) \\\end{align*}
最後に、本節で述べた内容に関してのプログラムを作成する。
Unityで内積を求める場合には次のメソッドが用意されている。
[Code1] (実行結果 図39)
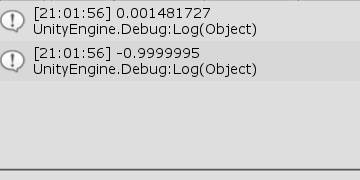
図39 3行目の Dot(..)には引数として v1.normalized、v2.normalized が指定されているが、これによりベクトルv1、v2の単位ベクトルの内積が算出される。図39の実行結果では、最初の計算の内積が 0.0014... となっており、非常に $0$に近い値である。本節 B) の「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が $0$であるときは、その2つのベクトルは直交している。つまり、最初の計算における v1、v2のなす角は非常に$90$°に近いということがわかる。
第2の計算は v1、v2の値を変えて、再び単位ベクトルの内積を計算したものである。
実行結果は -0.9999... となっており、今度は非常に$-1$近いに値である。「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が$-1$であるときは、その2つのベクトルは平行であるが、向きは反対である。したがって、第2の計算における v1、v2のなす角は非常に$180$°に近いということがわかる。
各点の座標は $A = (2.77,\ 5.0,\ 2.36)$、$B = (3.05,\ 4.41,\ 4.25)$、$C = (2, 5, 3)$ である。
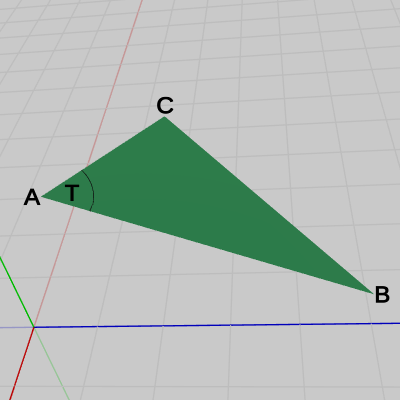
図40 △ABC と ∠T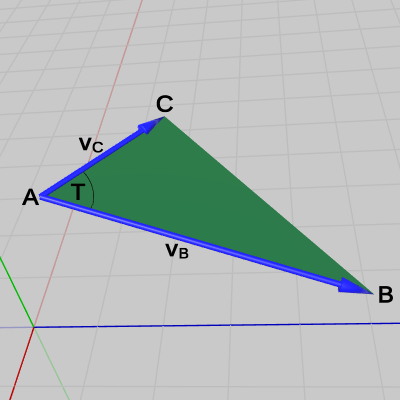 
図41 ベクトルvBとvC
まず先にプログラムを示す。
[Code2] (実行結果 図42)
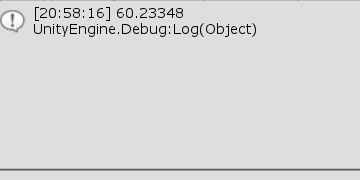
図42 Code2 実行結果 1行目から3行目の A、B、C は図における$A$、$B$、$C$の各位置を表している。4行目、5行目の vB は$A$を始点とし$B$を終点とするベクトル、vC は$A$を始点とし$C$を終点とするベクトルである (図41)。6行目において その2つのベクトルの単位ベクトルの内積を算出しているが、辺$AB$と辺$AC$のなす角は図に示されるように $\angle T$ であるから、この内積の値dotは $\cos T$に等しい (本節 B) の「ベクトルのなす角」参照)。
7行目の Acos(..) は $\cos$関数の逆関数で、$\cos\theta$から$\theta$を求める際に使用する (Mathf構造体のstaticメソッド)。6行目のdotは $\cos T$に等しいので、7行目の Acos(dot) によって返される値は角度$T$である。しかし、ここで注意することがある。Acos(..)から返される角度は弧度法の値($\pi / 2$、$\pi$ などで単位はラジアン)になっているという点である。
8行目では7行目で算出された radian に Mathf.Rad2Deg を掛けているが、これによって弧度法の値から度数法の値($30$°、$60$° など)に変換されるのである (Mathf.Rad2Degは、弧度法の値から度数法の値に変換するときに、弧度法の値に掛ける定数)。
実行結果(図42)では 60.23... と出力されているが、これは $\angle T$が約$60$°であることを示している。
A) ベクトルの内積
3D空間においては、ベクトルの内積は次のように定義される。ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$の内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2\]
(計算例)
ベクトル$\boldsymbol{\mathsf{v_1}} = (1, 2, 3)$と $\boldsymbol{\mathsf{v_2}} = (6, 5, 4)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 1\cdot6 + 2\cdot5 + 3\cdot4 = 6 + 10 + 12 = 28\] ベクトル$\boldsymbol{\mathsf{v_1}} = (3, -1, -5)$と $\boldsymbol{\mathsf{v_2}} = (0,\ 5, -1)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 3\cdot0 + (-1)\cdot5 + (-5)\cdot(-1) = 0 + (-5) + 5 = 0\]
定義から明らかなように、内積は以下のように積の順序について交換可能である。
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = \boldsymbol{\mathsf{v_2}}\cdot\boldsymbol{\mathsf{v_1}}\]
また、同じベクトル同士の内積、例えばベクトル$\boldsymbol{\mathsf{v}} = (x, y, z)$同士の内積は、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = xx + yy + zz = x^2 + y^2 + z^2\] となるが、これはベクトル$\boldsymbol{\mathsf{v}}$の大きさ($|\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}$)の$2$乗に等しい。すなわち、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = |\boldsymbol{\mathsf{v}}|^2\] である。
B) ベクトルのなす角
ベクトルの内積は、ベクトルのなす角と密接な関係がある。すなわち、次の等式が成り立つ。ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$のなす角を $A$とし、$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の大きさを$|\boldsymbol{\mathsf{v_1}}|$、$|\boldsymbol{\mathsf{v_2}}|$とすれば
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2 = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\cos{A}\] である。
図1のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$は、両者のなす角が $A$である。図2は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である(両者のなす角は変わらない)。
上の等式における$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の代わりに単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$を式に使った場合、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = |\boldsymbol{u_1}||\boldsymbol{u_2}|\cos{A} \] となるが、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$は単位ベクトルであるから、$|\boldsymbol{u_1}|$、$|\boldsymbol{u_2}|$の値は$1$である。すなわち、\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} \] が成り立つ。
この結果は、2つのベクトルの単位ベクトルの内積を求めれば、その2つのベクトルのなす角を知ることが可能であることを意味している。
以下では、その特殊な例として2つのベクトルが直交している場合、あるいは平行である場合の判定方法について見ていく。
(注) 以下の例ではベクトルのなす角は、0°～180°の範囲にあるものとする。
(例1) 2つのベクトルが直交しているかどうかの判定(なす角が$90$°)
図3に示されるベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$のなす角を $A$とする。図4は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0\] 上で述べたように、単位ベクトルの内積はそれらのなす角の余弦($\cos$)に等しいから、結局\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 0\] となる。
$\cos{A} = 0$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 90$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$0$になる場合では、両者は直交していることがわかる(2つのベクトルが直交している場合は、両者を正規化せずに内積を計算しても結果は$0$になる。つまり、この例では$\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$の値も$0$である)。
(例2) 2つのベクトルが平行であるかどうかの判定 1 (なす角が$0$°)
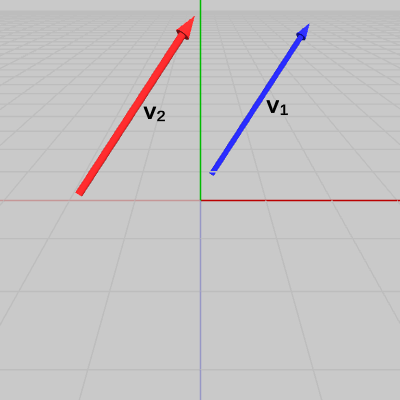図5 ベクトルv1、v2
図6 ベクトルv1、v2の始点を原点に移動させる
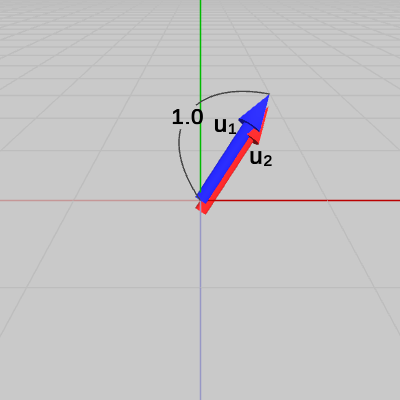図7 ベクトルv1、v2を正規化したu1、u2
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図5に示される位置に置かれている。この2つのベクトルのなす角は、両者の始点を原点に移動させたときの2つのベクトルのなす角のことである。今回の例では、2つのベクトルを原点に移動させたときに(図6)、2つのベクトルが重なってしまっているので角度の表示がされていないが、ここでも両者のなす角を$A$とする。
図7は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1\] 先程と同じように、両者のなす角の余弦($\cos$)を使って表せば、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 1\] となる。
$\cos{A} = 1$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 0$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$1$になる場合では、両者は平行でありベクトルの向きも同じであることがわかる。
(例3) 2つのベクトルが平行であるかどうかの判定 2 (なす角が$180$°)
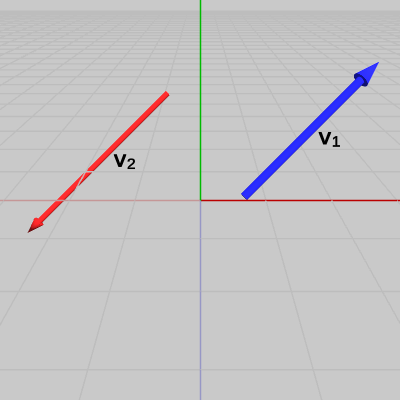図8 ベクトルv1、v2
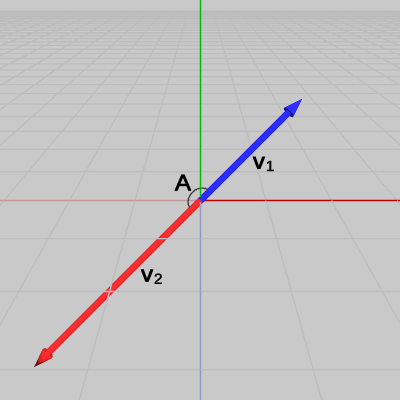図9 ベクトルv1、v2の始点を原点に移動させる
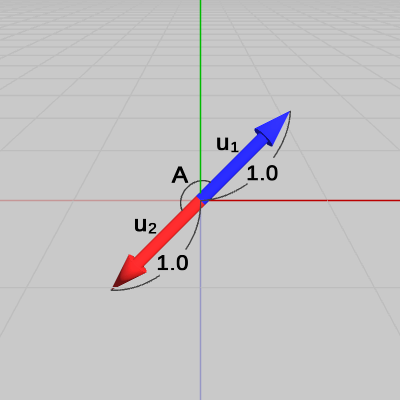図10 ベクトルv1、v2を正規化したu1、u2
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図8に示される位置に置かれている。この2つのベクトルのなす角は、上の例で述べたように両者の始点を原点に移動させたときの2つのベクトルのなす角のことであり、図9に示されるようにここでも両者のなす角を$A$とする。
図10は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = -1\] $\cos{A} = -1$ を満たす角度$A$は($0$°～$180$°の範囲では)、$A = 180$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$-1$になる場合では、両者は平行であるがベクトルの向きは逆向きであることがわかる。
以上をまとめると、2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ 及び、それらの単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積について次のことがいえる。
(ⅰ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0$ のとき、2つのベクトルは直交する。
(ⅱ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1$ のとき、2つのベクトルは平行であり同じ向きである。
(ⅲ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = -1$ のとき、2つのベクトルは平行であり逆向きである。
ここではベクトルのなす角の範囲を$0$°～$180$°の範囲に制限したが、この範囲を$0$°より下、あるいは$180$°より上の範囲に広げても上記の(ⅰ)～(ⅲ)は成立する。
C) 直線への垂線
図11には、点$P$と原点を通る直線$m$が示されている。今、点$P$から直線$m$に垂線をおろして、垂線と直線$m$の交点を$Q$とする。ここでは、この交点$Q$を内積を使って求めてみよう (2D空間の章ではある点から直線上へ垂線を下すことを「射影」と呼んだが、3D空間においても同様である。以下の点$Q$は、点$P$を直線$m$へ射影したときの像である)。 (以下では原点を$O$で表す。)
原点$O$を始点、点$P$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とする。また、直線$m$の方向(原点$O$から点$Q$へ向かう方向)を表す単位ベクトルを$\boldsymbol{u}$とし、その始点を原点に置く。ベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$のなす角を $A$とする(以上は図13参照)。
ここでベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$の内積を計算すると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}||\boldsymbol{u}|\cos{A} = |\boldsymbol{\mathsf{v}}|\cos{A}\] であるが、この $|\boldsymbol{\mathsf{v}}|\cos{A}$ が何を表すかについて図14を用いて説明しよう。
図14では原点$O$と点$P$、$Q$を結んだ三角形(直角三角形)の各辺に記号がふられてある。これは各辺の長さを表し、すなわち辺$OP$の長さが$a$、辺$PQ$の長さが$b$、辺$OQ$の長さが$c$である。ベクトル$\boldsymbol{\mathsf{v}}$は、$O$と$P$を結ぶベクトルであるから、$\boldsymbol{\mathsf{v}}$の大きさ $|\boldsymbol{\mathsf{v}}|$ は辺$OP$の長さに等しい、すなわち $|\boldsymbol{\mathsf{v}}| = a$ である。
そして、$\triangle{OPQ}$は直角三角形であるから辺$OP$と辺$OQ$の長さについて次の関係が成り立つ。
\[ a\cos{A} = c \] 以上から、
\[ |\boldsymbol{\mathsf{v}}|\cos{A} = c \] つまり $|\boldsymbol{\mathsf{v}}|\cos{A}$ は辺$OQ$の長さに等しいことがわかる。原点$O$から点$Q$の方向を表す単位ベクトルは$\boldsymbol{u}$で、原点$O$から点$Q$までの長さが $|\boldsymbol{\mathsf{v}}|\cos{A}$ であるから、点$Q$の位置は
\[ Q = (|\boldsymbol{\mathsf{v}}|\cos{A})\boldsymbol{u} \] で求められる。
D) 座標系における座標値
C)では、3D空間内の点から原点を通る直線上へおろされた垂線の足(直線との交点)を求める問題を扱った。ここで扱う内容は、その延長的な内容である。C)において垂線の足である点$Q$を求める過程を再度見直してみよう。
原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$と、直線$m$の方向を表す単位ベクトル$\boldsymbol{u}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}|\cos{A}$ は、原点$O$から点$Q$までの長さに等しいのであった。そして、原点から直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れた位置に、点$P$からの垂線の足である点$Q$はあるのであった。このことを便宜上、「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」という言い方で表す(つまり点$P$の直線$m$方向の距離とは、原点から(垂線の足)点$Q$までの距離である)。
以上をふまえて本題に入る。
点$P$の座標が$(4, 3, 2)$であるとは、点$P$を図16のように原点に置いてから、まず始めにx軸方向に$4$移動させ(図17)、次にy軸方向に$3$移動させ(図18)、そして最後にz軸方向に$2$移動させる(図15)、この原点からの3回の移動後の$P$の位置のことを意味している。
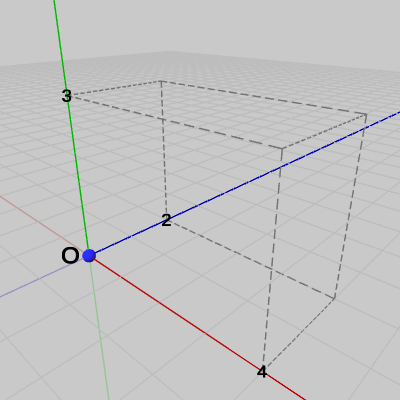図16 点P = (0, 0, 0)
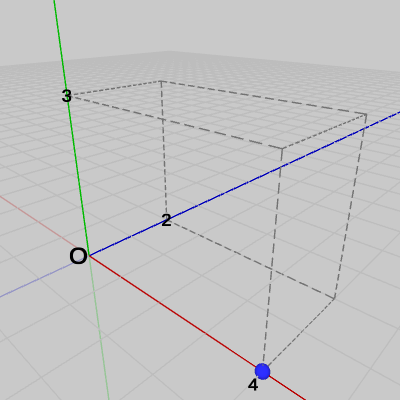図17 (0, 0, 0)からx軸方向に4移動 (点Pは(4, 0, 0)に移動する)
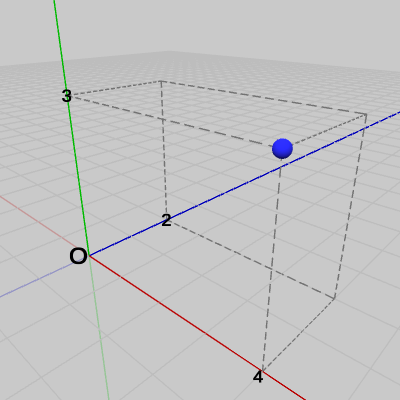図18 (4, 0, 0)からy軸方向に3移動 (点Pは(4, 3, 0)に移動する)
言い換えれば、点の座標値における各座標(x座標、y座標、z座標)は、その点が原点から各軸の方向にどれだけ離れているかを表している。点$P = (4, 3, 2)$の場合でいえば、点$P$が原点からx軸方向に$4$、y軸方向に$3$、z軸方向に$2$だけ離れていることを表している。
点$P$が原点からx軸方向、y軸方向、z軸方向にどれだけ離れているかは図15を見ればわかるが、ここでは内積を使ってその距離を計算してみよう。
そのために原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と、x軸、y軸、z軸の各方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$、$\boldsymbol{u_y} = (0, 1, 0)$、$\boldsymbol{u_z} = (0, 0, 1)$を用意する(図19、図20)。
まず、点$P$が原点からx軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とx軸方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_x}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} = 4\cdot1 + 3\cdot0 + 2\cdot0 = 4\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \]
点$P$からx軸へ垂線をおろし、その足を点$Q_x$とする($\triangle{OPQ_x}$は直角三角形になる)。C)で見たように、原点$O$から点$Q_x$までの距離は、原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$とx軸方向の単位ベクトル$\boldsymbol{u_x}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} (= |\boldsymbol{\mathsf{v}}|\cos{A})$ であるが、これは上で求めたとおり $4$ である。
先程、C)の点$P$について次のような言い方を用いた。「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」。この表現を今の例にあてはめると、直線$m$はx軸に相当し、ここでの$|\boldsymbol{\mathsf{v}}|\cos{A}$は$4$であるので、「点$P$はx軸の方向に$4$だけ離れている」という内容になる。
点$P$が原点からx軸方向にどれだけ離れているかを内積を使って求めるというのが、ここでの目的であったが、今述べてきたことがそれにあたるわけである。
点$P$のy軸方向の距離、z軸方向の距離についても同様の手順で求めることができる。
図22に示されるようにy軸方向の距離は、点$P$からy軸におろした垂線の足を点$Q_y$とすれば、原点から$Q_y$までの距離のことである($\triangle{OPQ_y}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とy軸方向を表す単位ベクトル$\boldsymbol{u_y} = (0, 1, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_y}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_y} = 4\cdot0 + 3\cdot1 + 2\cdot0 = 3\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \] x軸の場合と同様に、この結果は「点$P$はy軸の方向に$3$だけ離れている」ことを意味している。
図23に示されるようにz軸方向の距離は、点$P$からz軸におろした垂線の足を点$Q_z$とすれば、原点から$Q_z$までの距離のことである($\triangle{OPQ_z}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とz軸方向を表す単位ベクトル$\boldsymbol{u_z} = (0, 0, 1)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_z}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_z} = 4\cdot0 + 3\cdot0 + 2\cdot1 = 2\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \] この結果は「点$P$はz軸の方向に$2$だけ離れている」ことを意味している。
だが、以上に述べてきた事柄はおそらく自明過ぎるものであろう。x軸、y軸、z軸のような基本的な座標軸上での点の位置は、そもそも点の座標値から分かることであって、わざわざ内積を使ってまで求める必要はない。確かに今まで用いてきた座標系(と座標値)ならばそれはいえる。しかし、例えばこの同じ点$P$を図24に示されるような水色、紫色、黄色の座標軸を持つ傾いた座標系を基準にした場合などでは、いささか状況が異なってくる。
図24に示される座標系は互いに直交する i軸(水色)、j軸(紫色)、k軸(黄色)によって構成される座標系で、便宜上ここでは ijk座標系と呼ぶことにする(図25はやや離れた位置から ijk座標系を見たもの。また、i軸、j軸、k軸についてはプラス側のみ表示してある)。そして、今まで用いてきた x軸、y軸、z軸の座標系の方をxyz座標系と呼ぶことにする。
図からわかる通り ijk座標系は傾いた座標系であり、xyz座標系とは原点が一致している。
今から問題とするのは、上で使ってきた点$P$の ijk座標系における座標値の計算である。すなわち、点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離を求めることであり、それは図26における点線の直方体の3つの辺の長さ$a$、$b$、$c$を求めることと同じである(図27は見やすくするためにxyz座標系を取り除いたもの。図における点線の図形は直方体であるので隣接する面の間の角度は直角である)。
xyz座標系における$P$の座標は$(4, 3, 2)$であったが、ijk座標系での座標は図27を見ると、そのような整数値でないことは明らかである(もちろん点$P$の位置は今までの位置から動かしていない)。
しかし、点$P$の ijk座標系における座標を計算するのは難しいことではない。今まで見てきたことをなぞっていけば、自ずと答えが導かれる。ただし、注意すべきことが1つある。今、座標系が2つ出てきたが、この先で使用する、原点と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$、i軸、j軸、k軸の方向を表す単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$などは全てxyz座標系での値である。例えば、何度も出てきたが$(4, 3, 2)$という点$P$の座標はxyz座標系での値である。ijk座標系では図26(あるいは図27)に示されるように点$P$は$(a, b, c)$であり、$(4, 3, 2)$ではない (これは 点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離が $a$、$b$、$c$ であり $4$、$3$、$2$ ではないことを意味する)。
計算手順については今までと同様である。
まず、原点$O$から点$P$へのベクトル$\boldsymbol{\mathsf{v}}$を用意する(図28)。xyz座標系での値であるので、今までどおり、$\boldsymbol{\mathsf{v}} = (4, 3, 2)$である。また、i軸方向、j軸方向、k軸方向の単位ベクトルを$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$とする(図29。図からわかるようにこれらもxyz座標系での値であり、小数3位以下を省略してある)。
図の緑色の数値はベクトルの内容を表している。
(以下で使用される単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$は小数第3位以下を省略した値であるため、それらを使った計算結果もわずかな誤差を含んでいる。)
では、点$P$が原点から i軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と i軸方向を表す単位ベクトル$\boldsymbol{u_i} = (0.94, 0.12, 0.31)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_i}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_i} = 4\cdot0.94 + 3\cdot0.12 + 2\cdot0.31 = 4.74\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \]
この値が表すのは、図30に示されるように点Pから i軸におろした垂線の足を点$Q_i$とすれば、原点から$Q_i$までの距離のことである($\triangle{OPQ_i}$は直角三角形になる)。図30はxyz座標系でこの状況を示したものだが、図31のように ijk座標系のみで表示すると上の計算で何を求めたのかがより明らかになるだろう。原点から$Q_i$までの距離は、すなわち点$P$の i軸方向の距離のことであり、図31に示される辺の長さ$a$に等しい。つまり、点$P$の ijk座標系での i座標は $a = 4.74$ である。 点$P$が原点から j軸方向にどれだけ離れているかについても同様に計算してみよう。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と j軸方向を表す単位ベクトル$\boldsymbol{u_j} = (0.02, 0.91, -0.42)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_j}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_j} = 4\cdot0.02 + 3\cdot0.91 + 2\cdot(-0.42) = 1.97\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \]
この値が表すのは、図32に示されるように点Pから j軸におろした垂線の足を点$Q_j$とすれば、原点から$Q_j$までの距離のことである($\triangle{OPQ_j}$は直角三角形になる)。図33はこの様子を ijk座標系のみで表示したものである。原点から$Q_j$までの距離は、すなわち点$P$の j軸方向の距離のことであり、図33に示される辺の長さ$b$に等しい。つまり、点$P$の ijk座標系での j座標は $b = 1.97$ である。 点$P$のk軸方向の距離についても同様の手順を繰り返せばよい。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とk軸方向を表す単位ベクトル$\boldsymbol{u_k} = (-0.34, 0.40, 0.85)$の内積は、
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_k}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_k} = 4\cdot(-0.34) + 3\cdot0.40 + 2\cdot0.85 = 1.54\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \]
この値が表すのは、図34に示されるように点Pからk軸におろした垂線の足を点$Q_k$とすれば、原点から$Q_k$までの距離のことである($\triangle{OPQ_k}$は直角三角形になる)。図35はこの様子を ijk座標系のみで表示したものである。原点から$Q_k$までの距離は、すなわち点$P$のk軸方向の距離のことであり、図35に示される辺の長さ$c$に等しい。つまり、点$P$の ijk座標系でのk座標は $c = 1.54$ である。\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_k} = 4\cdot(-0.34) + 3\cdot0.40 + 2\cdot0.85 = 1.54\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \]
以上の結果をまとめると、点$P$の ijk座標系における座標(i座標、j座標、k座標)は、
\[P = (4.74,\ 1.97,\ 1.54)\]であることがわかった(図36)。
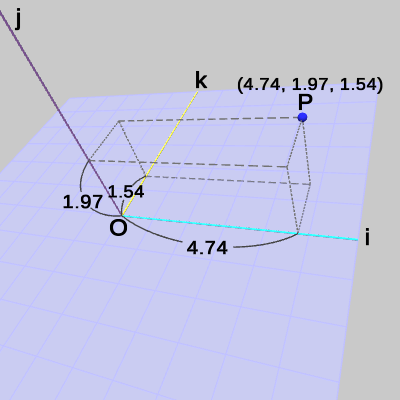図36 ijk座標系における点P = (4.74, 1.97, 1.54)
図37 xyz座標系における点P = (4, 3, 2)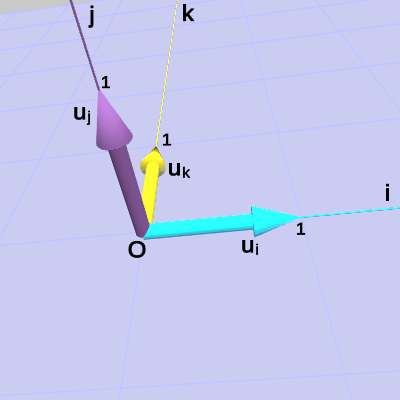
図38 ijk座標系における単位ベクトルui, uj, uk
比較のために図37にxyz座標系での点$P$を示す。
また、今までの計算で使われてきた単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$の値はxyz座標系での値であったが参考のために ijk座標系での値を以下に示しておこう(図38参照。以下のカッコの中の数値は i座標、j座標、k座標の順である)。
\begin{align*}\boldsymbol{u_i} = (1, 0, 0) \\\boldsymbol{u_j} = (0, 1, 0) \\\boldsymbol{u_k} = (0, 0, 1) \\\end{align*}
最後に、本節で述べた内容に関してのプログラムを作成する。
# Code1
最初のプログラムでは、2つのベクトルを単位ベクトル化してそれらの内積を求める。Unityで内積を求める場合には次のメソッドが用意されている。
Vector3.Dot(Vector3 v1, Vector3 v2)
: 引数に指定される2つのベクトルの内積を計算する Vector3構造体のstaticメソッド (戻り値は float型)。[Code1] (実行結果 図39)
Vector3 v1 = new Vector3(1.77f, 0.80f, -0.48f); Vector3 v2 = new Vector3(-2.06f, 5.45f, 1.45f); float dot = Vector3.Dot(v1.normalized, v2.normalized); Debug.Log(dot); v1 = new Vector3(3.17f, -1.29f, -2.07f); v2 = new Vector3(-3.97f, 1.61f, 2.59f); dot = Vector3.Dot(v1.normalized, v2.normalized); Debug.Log(dot);
第2の計算は v1、v2の値を変えて、再び単位ベクトルの内積を計算したものである。
実行結果は -0.9999... となっており、今度は非常に$-1$近いに値である。「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が$-1$であるときは、その2つのベクトルは平行であるが、向きは反対である。したがって、第2の計算における v1、v2のなす角は非常に$180$°に近いということがわかる。
# Code2
では次に、図40に示される$\triangle ABC$内の$\angle T$を求める問題について考える。各点の座標は $A = (2.77,\ 5.0,\ 2.36)$、$B = (3.05,\ 4.41,\ 4.25)$、$C = (2, 5, 3)$ である。
まず先にプログラムを示す。
[Code2] (実行結果 図42)
Vector3 A = new Vector3(2.77f, 5.0f, 2.36f); Vector3 B = new Vector3(3.05f, 4.41f, 4.25f); Vector3 C = new Vector3(2.0f, 5.0f, 3.0f); Vector3 vB = B - A; Vector3 vC = C - A; float dot = Vector3.Dot(vB.normalized, vC.normalized); float radian = Mathf.Acos(dot); float deg = radian * Mathf.Rad2Deg; Debug.Log(deg);
7行目の Acos(..) は $\cos$関数の逆関数で、$\cos\theta$から$\theta$を求める際に使用する (Mathf構造体のstaticメソッド)。6行目のdotは $\cos T$に等しいので、7行目の Acos(dot) によって返される値は角度$T$である。しかし、ここで注意することがある。Acos(..)から返される角度は弧度法の値($\pi / 2$、$\pi$ などで単位はラジアン)になっているという点である。
8行目では7行目で算出された radian に Mathf.Rad2Deg を掛けているが、これによって弧度法の値から度数法の値($30$°、$60$° など)に変換されるのである (Mathf.Rad2Degは、弧度法の値から度数法の値に変換するときに、弧度法の値に掛ける定数)。
実行結果(図42)では 60.23... と出力されているが、これは $\angle T$が約$60$°であることを示している。
© 2020-2024 Redpoll's 60 (All rights reserved)