Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-15
第2章 2D空間におけるオブジェクトの運動
$§$2-15 衝突判定 3
前節までの衝突判定では対象となるオブジェクトは円盤や長方形といった最も単純な形状のものであり、衝突判定の内容も円盤中心からの距離や、長方形の2つの頂点の各成分との大小比較といった単純なものであった。
本節では衝突判定の対象をより一般のオブジェクトにまで広げる。一般のオブジェクトまでを衝突判定の対象とする場合には、衝突判定の内容は円盤や長方形の場合のように単純なものにはならない。
一般のオブジェクトの場合、衝突判定においては三角形が重要な役割を担うことになるがまずはその点について解説しよう。
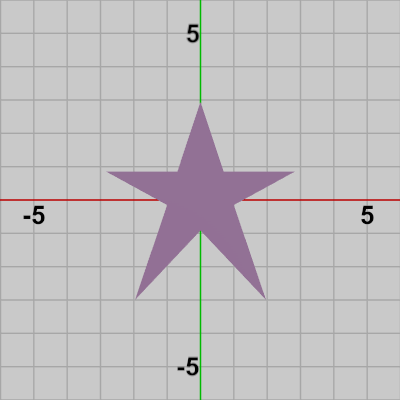
図1 Star 初期状態 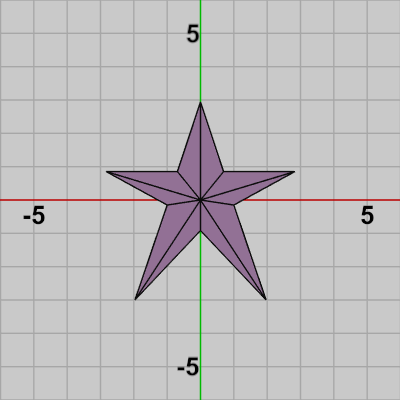
図2 Starを構成する三角形の集合
今、2D空間内を進んできたShellが図3に示されるように、Starのある位置に衝突したとしよう。これは別の見方をすれば図4に示されるように、Starを構成する三角形の1つに Shellが衝突したことと同じである。
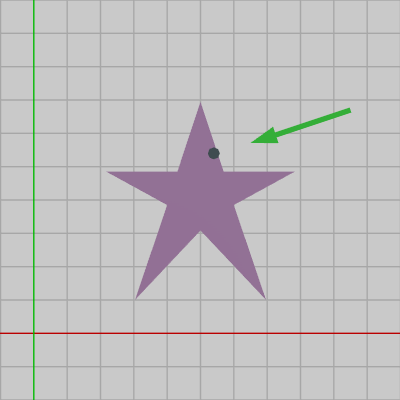
図3 StarにShellが衝突したときの様子 
図4 ShellはStarを構成する三角形の1つに衝突している
したがって、Shellが Starに衝突したかどうかの判定は、Shellが Starを構成する三角形のどれか1つと衝突したかを判定すればよいわけである。このことは Starだけでなく他の2Dオブジェクトにも言えることで、あるオブジェクトを三角形に分割し、そのオブジェクトを複数の三角形の集合とみなすと、Shellがオブジェクトに衝突したかどうかの判定は、Shellがそのオブジェクトを構成する複数の三角形のいずれか1つと衝突したかを調べることに帰着するのである。
そこで当然次に考えるべき問題として、Shellと三角形の衝突判定はどのように行えばよいかという問題が生じてくるわけである。
(以下では便宜上 三角形の集合として表されるオブジェクトを「TriMesh」と表記する)
Shellと三角形オブジェクトTriangleとの間に起こった衝突の検出には、以下のメソッドが使用される。
(注 : 点と三角形の集合との衝突判定用として使われる以下のメソッドは、長い間 for文内の3つのif文において、いずれも「$0$ より下」である場合に衝突として扱う実装であった。しかし一般には3つのif文判定では、いずれも「$0$ より上」である場合に衝突として扱う実装の方が多いため、そのように変更されている。もちろん以前のコードが誤りというわけではない。 2023.9 )
[CollisionTest_Point_TriMesh(..)]
3行目のfor文内の処理が先程述べた Edge Function の実装であるが、ここではメソッドの使用方法について解説しよう。
第1引数の P は Shellの位置である。メソッドの第2引数 crds はオブジェクトを構成する全ての三角形の頂点座標である。1次元配列であり、オブジェクトが三角形1つで構成されている場合(ただの三角形オブジェクトの場合)、crdsの内容はその三角形オブジェクトの3つの頂点座標のみであり、配列の要素数は $3$ である。オブジェクトが三角形2つで構成されている場合(四角形オブジェクトの場合)、crdsの内容は2つの三角形の全頂点の座標となり、配列の要素数は $3\times2 = 6$ である。同様に、オブジェクトが三角形10個で構成されているならば crds の内容は10個の三角形の全頂点の座標となり、配列の要素数は $3\times10 = 30$ である。
CollisionTest_Point_TriMesh(..) は Shellの位置 P (正確にはShellの中心座標)が、オブジェクトを構成する複数の三角形のいずれか1つに含まれている場合に true を返す。
つまり、三角形との衝突判定は Shell(の中心座標)が三角形に含まれているかどうかを調査するものであり、含まれている場合に衝突とみなされる。
3行目のforループは1回のループで1つの三角形との衝突判定を行うので、オブジェクトが10個の三角形によって構成されている場合、forループは最大10回繰り返される (途中で衝突が検出された場合はそこでtrueが返され、ループが終了する)。
2-14節から2-17節で使われる2Dオブジェクトはカスタムライブラリの THAlphaObject2D クラスのインスタンスであるが、そのうちで、円盤や長方形でないオブジェクトは複数の三角形の集合(TriMesh)として構成されている (正確には1つ以上の三角形の集合)。そして、そのようなオブジェクトを構成する全ての三角形の頂点座標は以下のプロパティによって取得することができる。
initTriangleCoords から返される座標配列はオブジェクトの初期状態における座標である。この initTriangleCoords と上記の CollisionTest_Point_TriMesh(..) を用いることで、Shellと三角形との衝突判定は次のように行われる。
図5は三角形オブジェクトTriangleの初期状態であり、ここでは各頂点に $A$、$B$、$C$ とラベルが付けられている。図6の Triangleには、$130$°の回転、$(-3.3,\ 2.2)$ だけの平行移動がこの順序で実行されており、このTriangleに向かって Shellが進んでいる。図7は図6から一定時間が経過したときのもので、Shellが Triangleに衝突したときの様子である。
Triangleに実行された回転、平行移動を表す変換行列を $R$、$T$ とし、その積を $M = TR$ とする。そして、図7の状態の Triangle、Shellの両者に対して、変換行列 $M$ の逆行列 $M^{-1}$ を実行する。\[ M^{-1} = (TR)^{-1} = R^{-1}T^{-1} \]であるから、逆行列 $M^{-1}$ の内容は、$(3.3, -2.2)$ だけの平行移動、$-130^\circ$ の回転をこの順序で実行するものである。以下の図8は図7の状態から $(3.3, -2.2)$ だけの平行移動を実行した結果であり、図9は さらに続けて $-130^\circ$ の回転を実行した結果である。
図9では Triangleが初期状態に戻っており、Shellは初期状態のTriangleに衝突した状態になっている。そして、Shellと Triangleとの衝突判定はこの状態において行うが、それはプログラムでは次のような記述になる。
1行目の shell_pos はShellの現在位置のことで、図7におけるShellの位置を表すものである。2行目の mtx は、Triangleに実行された変換行列のことで上の文章中における $M$ と同じものである。3行目の mtx.inverse は文章中における $M^{-1}$ と同じものであり、mtx.inverse と同次座標化された shell_pos との積を求め P にセットしているが、この P が表す位置は、図9におけるShellの位置 $P$ である。4行目の衝突判定メソッド CollisionTest_Point_TriMesh(..) は上で述べたように、(1つ以上の)三角形の集合の中に Shellの位置 P が含まれるかを判定するものである。Triangle.initTriangleCoords によって 初期状態におけるTriangleの各頂点の座標が配列の形で返され、その座標配列と P を用いて衝突判定が行われる。今回の例では4行目の initTriangleCoords で返される配列の内容は図5、図9に示される初期状態のTriangleの各頂点 $A$、$B$、$C$ の座標である。
繰り返しになるが、この衝突判定では図7の状態から Triangleに対して、現在実行されている変換行列の逆行列を実行して Triangleを初期状態に戻すが、このとき同時に Shellに対しても同じ逆行列を実行しているので、両者に逆行列を実行した結果は図9に示されるように、Shellが初期状態のTriangleに衝突した状態になる。そして、この状態で衝突判定を行うが、そのときに使われるメソッド CollisionTest_Point_TriMesh(..) で必要なデータは、Shellの位置と三角形の各頂点の座標(配列)である。「初期状態のTriangleに衝突した状態」でのShellの位置は上記のように Triangleの逆行列との積によって求める必要があるが、三角形の各頂点の座標については計算する必要はない。衝突判定は初期状態のTriangleを使って行われるので、initTriangleCoords が返す配列をそのまま使えばよいのである。衝突判定をオブジェクトの初期状態に戻して考えるのはそのためである。
衝突判定を初期状態で行わずに現在位置で行う場合、すなわち図9の状態ではなく図7の状態で衝突判定を行う場合には、図7の状態のTriangleの各頂点の座標を計算する必要がある。そのためには初期状態の各頂点のそれぞれに現在Triangleに実行されている変換行列を掛ける必要がある。Triangleならば頂点数は3個であるから変換行列との積は3回で済むが、もし 衝突判定対象のオブジェクトが複数の三角形で構成されている場合、それらの三角形の(初期状態の)全頂点と変換行列との積を計算しなければならない。三角形10個で構成されていれば30回の計算であり、三角形100個で構成されていれば300回の計算になる (オブジェクトが運動している場合にはその計算は毎フレーム行わなければならない)。逆行列によって初期状態のオブジェクトに戻して衝突判定を考える場合には、Shellの位置を算出するだけであり1回の計算で済むのである。
先程使用した星形オブジェクト Starを例にとって話を進める。

図10 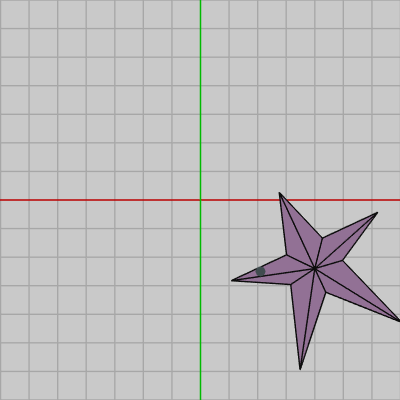
図11
図10は、Starに何らかの変換行列が実行されており、そのStarに対して Shellが衝突したときの様子である。図11はその状態において、Starを三角形に分割して表示したものである。
このときの Shellと Starの衝突判定のプログラムは次のようなものになる。
このプログラムは上で見た三角形との衝突判定プログラムとほとんど同じである。上のプログラムとの違いは、2行目、4行目で Triangle となっていた部分がここでは Star となっている点のみである。
1行目のローカル変数 shell_pos は Shellの現在位置の座標である。2行目の mtx は Starに実行された変換行列であり、3行目の計算は Starの逆行列 mtx.inverse と shell_pos との積によって、「初期状態のStarに衝突した状態」でのShellの位置を計算している。4行目の initTriangleCoords によって、Starを構成する全ての三角形の(初期状態の)頂点座標が配列の形で返されるが、Starは10個の三角形によって構成されているのでその要素数は $3\times10 = 30$ である。
下の図でいえば、1行目の shell_pos は図11における Shellの位置を表している。下図12は図11の状態から、Starに実行された変換行列の逆行列を Star及び Shellの両者に実行した結果であるが、これによって Starは初期状態に戻り、Shellは初期状態のStarに衝突した状態になっている。上のプログラム 3行目の P は図12における Shellの位置 $P$ を表している。4行目の initTriangleCoords は Starを構成する三角形の頂点座標配列が返されるが、それは図12の初期状態における全三角形の頂点座標配列である。したがって、4行目の CollisionTest_Point_TriMesh(..) では図12におけるShellの位置 $P$ が、図12のStarを構成する三角形のどれか1つに含まれているかどうかを調べることになる。

図11 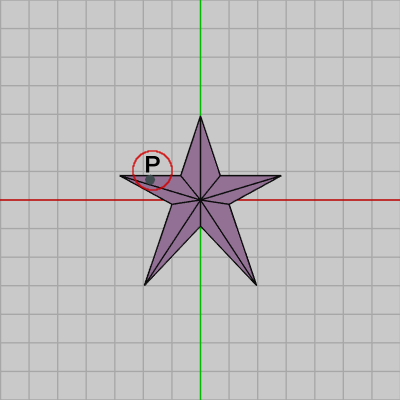
図12
繰り返しになるが、一般のオブジェクトとの衝突は単一の三角形との衝突判定と内容的には同じものである。それは一般のオブジェクトが複数の三角形で構成されているためである。そして、衝突判定はそのオブジェクトを初期状態に戻した状態で考えるため、衝突判定の際に必要となるのは オブジェクトを初期状態に戻した際のShellの位置、及びそのオブジェクトを構成する全ての三角形の初期状態における頂点座標の配列である。その2つのデータを取得した後は一般オブジェクト用の衝突判定メソッド CollisionTest_Point_TriMesh(..) へそれらを引数として渡すだけである。
ここからは本節の内容に関連したプログラムを作成する。
前節と同様に本節においても、Shellは飛行機オブジェクト Planeから発射され、シーン内に配置されているオブジェクトとの間において衝突判定が行われる。
また、本節での Planeの運動及び、Planeから発射される Shellの運動については前節 Code2 と同じ内容になるため、ここでもそれを利用する。すなわち、次のコードである。
[2-14節 Code2]
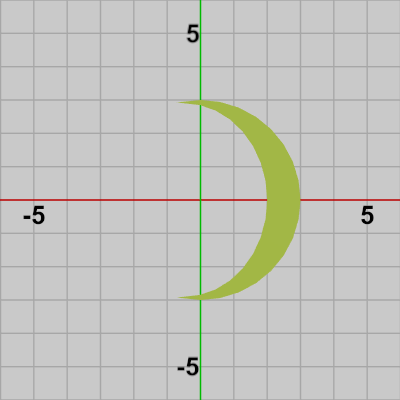
図13 Moon 初期状態 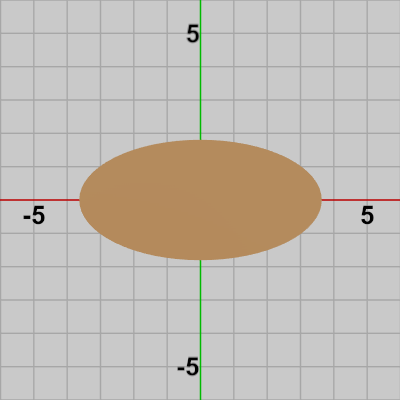
図14 Ellipse 初期状態
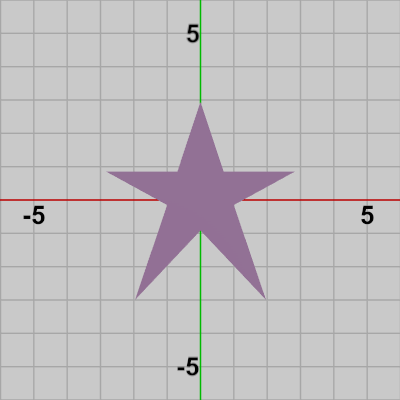
図15 Star 初期状態 
図16 Letter 初期状態
これらのオブジェクトはいずれも以下に示されるように、三角形の集合として構成されている (図18のEllipseは$64$個の三角形で構成されており、全ての三角形の先端が原点にあるため原点付近が黒つぶれした表示になってしまっている)。
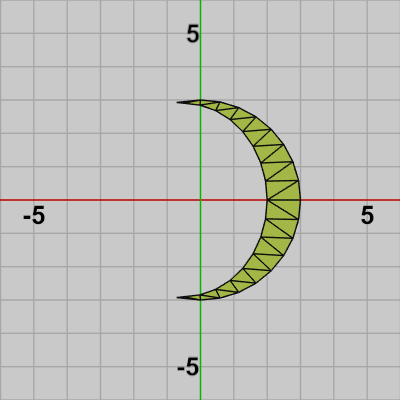
図17 Moonを構成する三角形の集合 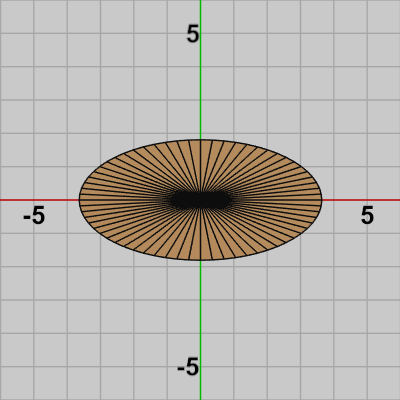
図18 Ellipseを構成する三角形の集合
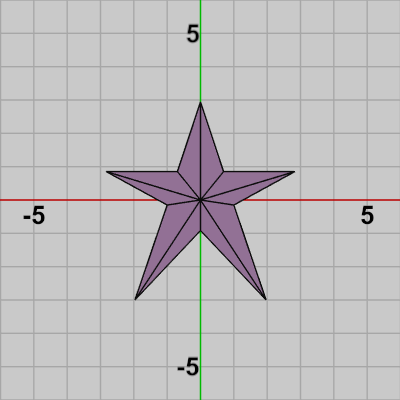
図19 Starを構成する三角形の集合 
図20 Letterを構成する三角形の集合
これら4つのオブジェクトを2D空間内の適当な位置に配置して、Shellとこれらのオブジェクトとの間における衝突判定を実装しよう。
実際のプログラムは次のとおり。
[Code1] (実行結果 図21)

図21 Code1 実行結果 先程述べたように、Plane運動及び Planeから発射されるShellの運動についての記述は 2-14節 Code2 と同じである (上記プログラム44行目まで)。Shellについても発射のたびにキーを押す単発の発射であり、プログラム内では「OneShell」の名前で使われている。
47行目から57行目で 4つのオブジェクトを適当な位置に配置している。ここで使われている c_posMoon、c_posEllipse、c_posStar、c_posLetter はそれぞれのオブジェクトが配置される位置を表す Vector2型の定数である。
59行目以降が衝突判定処理である。今回は衝突判定の対象となるオブジェクトが4つであるため、62行目の foreachループ内でその1つ1つと、Shellが衝突したかどうかを調べている。62行目の i_collisionObjects は衝突判定の対象となる4つのオブジェクトがセットされている配列(インスタンス変数)であり、以下のようにセットされている。衝突判定はオブジェクトが複数になったために foreach文が使われているが、その内容は本節の解説で見てきたものと特に変わるところはない。
[Code2] (実行結果 図22)

図22 Code2 実行結果 47行目から64行目までがオブジェクトの運動の記述であり、各オブジェクトが指定の位置で回転を行うようにするだけの処理である。67行目以降が衝突判定処理であるが、Code1と全く同じである。
オブジェクトが静止していても運動をしていても、そのオブジェクトに実行されている逆行列によって、オブジェクトを初期状態に戻した状態で衝突判定を行うという処理は変わらない。ただし繰り返しになるが、実際にオブジェクトの逆行列が使われるのは、オブジェクトを初期状態に戻した際のShellの位置を求めるときのみである (プログラム72行目)。
なお、1点追記しておこう。
本節で使われたMoonやStarは、以下の図に示されるように先の尖った部分を持っている。こういったオブジェクトについては、場合によっては本節の方法では衝突が検出されないことがある。言い換えれば、オブジェクトが細い部分を持っている場合には、そういったオブジェクトの衝突判定には注意が必要である。

図23 Moon先端の細い部分 
図24 Star先端の細い部分
以下では Starを例にとって話を進める。

図25 図25のアニメーションは、本節で見てきたような衝突判定プログラムの実行結果である。Planeが Starに向けて Shellを発射するものであり、このアニメーションにおいては Shellは Star上部に衝突しているように見える。しかし、特に衝突したことを示すような変化(たとえば、Starの色の変化)が発生せず、Shellは Star上部を何事もなく通過していく。実行しているプログラムの衝突判定メソッドは本節のものと同じものであり、衝突判定をオフにしているわけでもない。
本節で解説した三角形との衝突判定や、2-13節で解説した円盤及び長方形との衝突判定のアルゴリズムはいわゆる内外判定に属すものである。内外判定とは、ある点がオブジェクトに含まれていれば衝突として扱うが、含まれていない場合には衝突とはみなさない。衝突の判定方法がこのような基準であると、次のようなケースでは衝突は検出されなくなる。以下に示す例は図25のアニメーションのある時点での様子である。

図26 
図27
図26は Planeから発射されたShellが、ある時点において図に示される位置$P$に進んだときのものである。ここでは、Shellの進行速度が1フレーム当たり $0.5$ であるとする。図27は図26からちょうど1フレーム後の様子であり、そのときの Shellの位置を $P'$ とする。図26から1フレーム経過したときのものなので図27の Shellの位置$P'$は図26の位置$P$から $0.5$ だけ離れているわけである。

図28 P、P' はStarの極めて近い位置あるが、Starに含まれているわけではない (2つの黄色い点は1フレーム分の距離 0.5 だけ離れている)。 図28はこの1フレーム分の移動の様子を拡大して表示したものである。$P$、$P'$ はShellの座標であるが、正確にはその中心座標のことで、図28の小さな黄色い点の位置のことである。図から明らかなように $P$ も $P'$ もStarの極めて近い位置にあるが、Starに含まれているわけではないので「オブジェクトに点が含まれているか」が基準となる内外判定では、$P$ も $P'$ もStarと衝突としたとはみなされない。
しかし、図25のアニメーションでは Shellは Starに衝突しているように見える。これは、フレームを連続的に表示したときにそう見えているだけで、フレームを1枚1枚見ていくと あるフレームにおいて Starの上部付近で Shellが位置$P$まで進んだとき、その次のフレームで Shellは位置$P'$に進んでいるのである。Shellがこのような進み方をする場合、フレームを連続的に表示したもの(図25のアニメーション)を見る限りでは衝突しているように見えるが、実際には Shellはその進行中に Starの近傍に来ることはあっても、Starに含まれることはないのである。このような理由で、図25では衝突が検出されていないのである。
つまり、オブジェクトのある部分がとても細く、Shellの1フレームあたりの移動距離よりも小さいときには、Shellがオブジェクトのその部分の近傍に進み、その次の移動で Shellがその部分を通り越した位置に移動することが起こり得るわけである。このような場合には、内外判定では衝突は検出されずに、Shellは何事なくオブジェクト上を通過していってしまう。
最後に一点。
本節のプログラムでは、Plane及び Shellの運動に関する記述は 2-14節のCode2と同じものであった。以降の衝突判定のプログラムにおいても、それは同様であるので、2-14節 Code2における Planeの運動に関する部分を UserMotion() という名前のメソッドとして以下のように独立させる。
[UserMotion()]
プログラムの記述量が増えてきたため、同じような記述はメソッド化してプログラムの可読性を保持していくための便宜的な措置である。
本節では衝突判定の対象をより一般のオブジェクトにまで広げる。一般のオブジェクトまでを衝突判定の対象とする場合には、衝突判定の内容は円盤や長方形の場合のように単純なものにはならない。
一般のオブジェクトの場合、衝突判定においては三角形が重要な役割を担うことになるがまずはその点について解説しよう。
A) オブジェクトの分割
一般に 2Dオブジェクトであれ、3Dオブジェクトであれ任意のオブジェクトは三角形に分割して三角形の集合として考えることができる。例えば下図1の2DオブジェクトStarは三角形に分割すると図2のように表示されるが、図2のStarは10個の三角形で構成されたオブジェクトとして考えることができる。

今、2D空間内を進んできたShellが図3に示されるように、Starのある位置に衝突したとしよう。これは別の見方をすれば図4に示されるように、Starを構成する三角形の1つに Shellが衝突したことと同じである。


したがって、Shellが Starに衝突したかどうかの判定は、Shellが Starを構成する三角形のどれか1つと衝突したかを判定すればよいわけである。このことは Starだけでなく他の2Dオブジェクトにも言えることで、あるオブジェクトを三角形に分割し、そのオブジェクトを複数の三角形の集合とみなすと、Shellがオブジェクトに衝突したかどうかの判定は、Shellがそのオブジェクトを構成する複数の三角形のいずれか1つと衝突したかを調べることに帰着するのである。
そこで当然次に考えるべき問題として、Shellと三角形の衝突判定はどのように行えばよいかという問題が生じてくるわけである。
(以下では便宜上 三角形の集合として表されるオブジェクトを「TriMesh」と表記する)
B) 点 対 三角形 (Point vs Triangle)
順序的にはここで三角形との衝突判定に関する解説が行われるべきであるが、現時点では三角形との衝突判定の具体的な手法、いわゆるアルゴリズムについては解説しない。本節及び次節において三角形との衝突判定で使われるアルゴリズムは Edge Function と呼ばれるもので、正確にはある座標が三角形に含まれるかどうかを判定するものである。Edge Function はベクトルの外積という3D空間の概念を必要とするため、その詳細についてはベクトルの外積の導入後の段階で解説する。Shellと三角形オブジェクトTriangleとの間に起こった衝突の検出には、以下のメソッドが使用される。
(注 : 点と三角形の集合との衝突判定用として使われる以下のメソッドは、長い間 for文内の3つのif文において、いずれも「$0$ より下」である場合に衝突として扱う実装であった。しかし一般には3つのif文判定では、いずれも「$0$ より上」である場合に衝突として扱う実装の方が多いため、そのように変更されている。もちろん以前のコードが誤りというわけではない。 2023.9 )
[CollisionTest_Point_TriMesh(..)]
bool CollisionTest_Point_TriMesh(Vector2 P, Vector2[] crds)
{
for (int idx = 0; idx < crds.Length; idx += 3)
{
Vector2 A = crds[idx];
Vector2 B = crds[idx + 1];
Vector2 C = crds[idx + 2];
Vector2 a = (P - A);
Vector2 b = (B - A);
if (a.x * b.y - a.y * b.x < 0.0f) { continue; }
a = (P - B);
b = (C - B);
if (a.x * b.y - a.y * b.x < 0.0f) { continue; }
a = (P - C);
b = (A - C);
if (a.x * b.y - a.y * b.x < 0.0f) { continue; }
return true;
}
return false;
}
3行目のfor文内の処理が先程述べた Edge Function の実装であるが、ここではメソッドの使用方法について解説しよう。
第1引数の P は Shellの位置である。メソッドの第2引数 crds はオブジェクトを構成する全ての三角形の頂点座標である。1次元配列であり、オブジェクトが三角形1つで構成されている場合(ただの三角形オブジェクトの場合)、crdsの内容はその三角形オブジェクトの3つの頂点座標のみであり、配列の要素数は $3$ である。オブジェクトが三角形2つで構成されている場合(四角形オブジェクトの場合)、crdsの内容は2つの三角形の全頂点の座標となり、配列の要素数は $3\times2 = 6$ である。同様に、オブジェクトが三角形10個で構成されているならば crds の内容は10個の三角形の全頂点の座標となり、配列の要素数は $3\times10 = 30$ である。
CollisionTest_Point_TriMesh(..) は Shellの位置 P (正確にはShellの中心座標)が、オブジェクトを構成する複数の三角形のいずれか1つに含まれている場合に true を返す。
つまり、三角形との衝突判定は Shell(の中心座標)が三角形に含まれているかどうかを調査するものであり、含まれている場合に衝突とみなされる。
3行目のforループは1回のループで1つの三角形との衝突判定を行うので、オブジェクトが10個の三角形によって構成されている場合、forループは最大10回繰り返される (途中で衝突が検出された場合はそこでtrueが返され、ループが終了する)。
2-14節から2-17節で使われる2Dオブジェクトはカスタムライブラリの THAlphaObject2D クラスのインスタンスであるが、そのうちで、円盤や長方形でないオブジェクトは複数の三角形の集合(TriMesh)として構成されている (正確には1つ以上の三角形の集合)。そして、そのようなオブジェクトを構成する全ての三角形の頂点座標は以下のプロパティによって取得することができる。
Vector2[] initTriangleCoords
: オブジェクトを構成する全ての三角形の頂点座標を1次元配列の形で取得する (返される座標は、そのオブジェクトの初期状態におけるものである)。initTriangleCoords から返される座標配列はオブジェクトの初期状態における座標である。この initTriangleCoords と上記の CollisionTest_Point_TriMesh(..) を用いることで、Shellと三角形との衝突判定は次のように行われる。
-
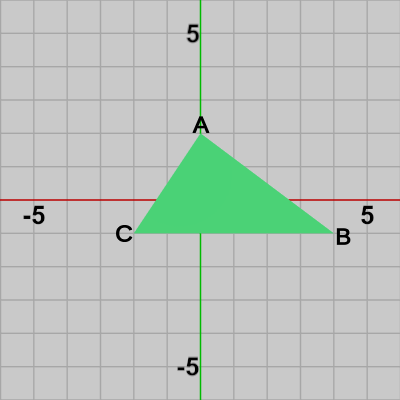 図5 Triangle 初期状態
図5 Triangle 初期状態 -
 図6 Triangleに向かってShellが進んでいる
図6 Triangleに向かってShellが進んでいる -
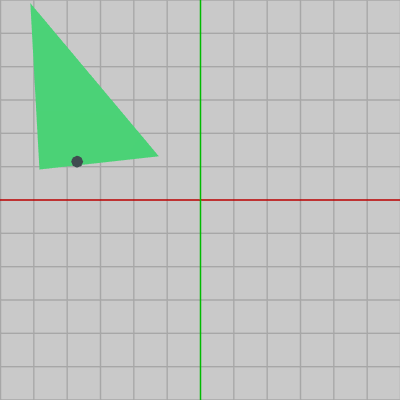 図7 ShellがTriangleに衝突したときの様子
図7 ShellがTriangleに衝突したときの様子
図5は三角形オブジェクトTriangleの初期状態であり、ここでは各頂点に $A$、$B$、$C$ とラベルが付けられている。図6の Triangleには、$130$°の回転、$(-3.3,\ 2.2)$ だけの平行移動がこの順序で実行されており、このTriangleに向かって Shellが進んでいる。図7は図6から一定時間が経過したときのもので、Shellが Triangleに衝突したときの様子である。
Triangleに実行された回転、平行移動を表す変換行列を $R$、$T$ とし、その積を $M = TR$ とする。そして、図7の状態の Triangle、Shellの両者に対して、変換行列 $M$ の逆行列 $M^{-1}$ を実行する。\[ M^{-1} = (TR)^{-1} = R^{-1}T^{-1} \]であるから、逆行列 $M^{-1}$ の内容は、$(3.3, -2.2)$ だけの平行移動、$-130^\circ$ の回転をこの順序で実行するものである。以下の図8は図7の状態から $(3.3, -2.2)$ だけの平行移動を実行した結果であり、図9は さらに続けて $-130^\circ$ の回転を実行した結果である。
-
 図7
図7 -
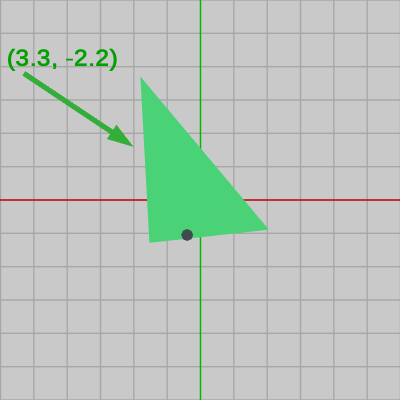 図8
図8 -
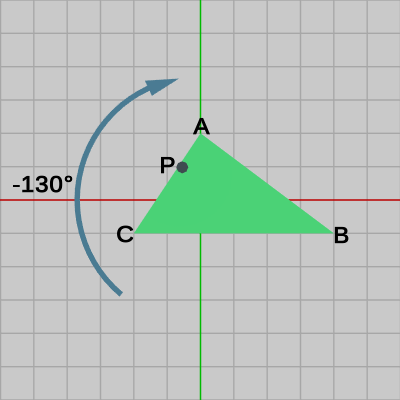 図9
図9
図9では Triangleが初期状態に戻っており、Shellは初期状態のTriangleに衝突した状態になっている。そして、Shellと Triangleとの衝突判定はこの状態において行うが、それはプログラムでは次のような記述になる。
Vector2 shell_pos = Shell.GetPosition(); THMatrix3x3 mtx = Triangle.GetMatrix(); Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos); bool bColl = CollisionTest_Point_TriMesh(P, Triangle.initTriangleCoords);
1行目の shell_pos はShellの現在位置のことで、図7におけるShellの位置を表すものである。2行目の mtx は、Triangleに実行された変換行列のことで上の文章中における $M$ と同じものである。3行目の mtx.inverse は文章中における $M^{-1}$ と同じものであり、mtx.inverse と同次座標化された shell_pos との積を求め P にセットしているが、この P が表す位置は、図9におけるShellの位置 $P$ である。4行目の衝突判定メソッド CollisionTest_Point_TriMesh(..) は上で述べたように、(1つ以上の)三角形の集合の中に Shellの位置 P が含まれるかを判定するものである。Triangle.initTriangleCoords によって 初期状態におけるTriangleの各頂点の座標が配列の形で返され、その座標配列と P を用いて衝突判定が行われる。今回の例では4行目の initTriangleCoords で返される配列の内容は図5、図9に示される初期状態のTriangleの各頂点 $A$、$B$、$C$ の座標である。
繰り返しになるが、この衝突判定では図7の状態から Triangleに対して、現在実行されている変換行列の逆行列を実行して Triangleを初期状態に戻すが、このとき同時に Shellに対しても同じ逆行列を実行しているので、両者に逆行列を実行した結果は図9に示されるように、Shellが初期状態のTriangleに衝突した状態になる。そして、この状態で衝突判定を行うが、そのときに使われるメソッド CollisionTest_Point_TriMesh(..) で必要なデータは、Shellの位置と三角形の各頂点の座標(配列)である。「初期状態のTriangleに衝突した状態」でのShellの位置は上記のように Triangleの逆行列との積によって求める必要があるが、三角形の各頂点の座標については計算する必要はない。衝突判定は初期状態のTriangleを使って行われるので、initTriangleCoords が返す配列をそのまま使えばよいのである。衝突判定をオブジェクトの初期状態に戻して考えるのはそのためである。
衝突判定を初期状態で行わずに現在位置で行う場合、すなわち図9の状態ではなく図7の状態で衝突判定を行う場合には、図7の状態のTriangleの各頂点の座標を計算する必要がある。そのためには初期状態の各頂点のそれぞれに現在Triangleに実行されている変換行列を掛ける必要がある。Triangleならば頂点数は3個であるから変換行列との積は3回で済むが、もし 衝突判定対象のオブジェクトが複数の三角形で構成されている場合、それらの三角形の(初期状態の)全頂点と変換行列との積を計算しなければならない。三角形10個で構成されていれば30回の計算であり、三角形100個で構成されていれば300回の計算になる (オブジェクトが運動している場合にはその計算は毎フレーム行わなければならない)。逆行列によって初期状態のオブジェクトに戻して衝突判定を考える場合には、Shellの位置を算出するだけであり1回の計算で済むのである。
C) 一般のオブジェクトとの衝突 (Point vs TriMesh)
一般のオブジェクトとの衝突についても、三角形との衝突の場合と事情は変わらない。それは、上でも述べたように一般のオブジェクトは複数の三角形の集合(TriMesh)として構成されているためである。先程使用した星形オブジェクト Starを例にとって話を進める。


図10は、Starに何らかの変換行列が実行されており、そのStarに対して Shellが衝突したときの様子である。図11はその状態において、Starを三角形に分割して表示したものである。
このときの Shellと Starの衝突判定のプログラムは次のようなものになる。
Vector2 shell_pos = Shell.GetPosition(); THMatrix3x3 mtx = Star.GetMatrix(); Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos); bool bColl = CollisionTest_Point_TriMesh(P, Star.initTriangleCoords);
このプログラムは上で見た三角形との衝突判定プログラムとほとんど同じである。上のプログラムとの違いは、2行目、4行目で Triangle となっていた部分がここでは Star となっている点のみである。
1行目のローカル変数 shell_pos は Shellの現在位置の座標である。2行目の mtx は Starに実行された変換行列であり、3行目の計算は Starの逆行列 mtx.inverse と shell_pos との積によって、「初期状態のStarに衝突した状態」でのShellの位置を計算している。4行目の initTriangleCoords によって、Starを構成する全ての三角形の(初期状態の)頂点座標が配列の形で返されるが、Starは10個の三角形によって構成されているのでその要素数は $3\times10 = 30$ である。
下の図でいえば、1行目の shell_pos は図11における Shellの位置を表している。下図12は図11の状態から、Starに実行された変換行列の逆行列を Star及び Shellの両者に実行した結果であるが、これによって Starは初期状態に戻り、Shellは初期状態のStarに衝突した状態になっている。上のプログラム 3行目の P は図12における Shellの位置 $P$ を表している。4行目の initTriangleCoords は Starを構成する三角形の頂点座標配列が返されるが、それは図12の初期状態における全三角形の頂点座標配列である。したがって、4行目の CollisionTest_Point_TriMesh(..) では図12におけるShellの位置 $P$ が、図12のStarを構成する三角形のどれか1つに含まれているかどうかを調べることになる。


繰り返しになるが、一般のオブジェクトとの衝突は単一の三角形との衝突判定と内容的には同じものである。それは一般のオブジェクトが複数の三角形で構成されているためである。そして、衝突判定はそのオブジェクトを初期状態に戻した状態で考えるため、衝突判定の際に必要となるのは オブジェクトを初期状態に戻した際のShellの位置、及びそのオブジェクトを構成する全ての三角形の初期状態における頂点座標の配列である。その2つのデータを取得した後は一般オブジェクト用の衝突判定メソッド CollisionTest_Point_TriMesh(..) へそれらを引数として渡すだけである。
ここからは本節の内容に関連したプログラムを作成する。
前節と同様に本節においても、Shellは飛行機オブジェクト Planeから発射され、シーン内に配置されているオブジェクトとの間において衝突判定が行われる。
また、本節での Planeの運動及び、Planeから発射される Shellの運動については前節 Code2 と同じ内容になるため、ここでもそれを利用する。すなわち、次のコードである。
[2-14節 Code2]
if (!i_INITIALIZED)
{
Plane.initShootPosition = new Vector2(0.0f, 2.1f);
Plane.initShootDirection = new Vector2(0.0f, 1.0f);
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Vector2 curP = Plane.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.12f * forwardDir : curP;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Plane.SetMatrix(M);
// Shell
if (Input.GetKeyDown(KeyCode.A))
{
Vector2 startPos = M * Plane.initShootPosition;
OneShell.SetPosition(startPos);
OneShell.direction = (M * Plane.initShootDirection).normalized;
}
else
{
Vector2 newShellPos = OneShell.GetPosition() + 0.50f * OneShell.direction;
OneShell.SetPosition(newShellPos);
}
# Code1
以下の図は4つのオブジェクト Moon、Ellipse、Star、Letter の初期状態である。



これらのオブジェクトはいずれも以下に示されるように、三角形の集合として構成されている (図18のEllipseは$64$個の三角形で構成されており、全ての三角形の先端が原点にあるため原点付近が黒つぶれした表示になってしまっている)。




これら4つのオブジェクトを2D空間内の適当な位置に配置して、Shellとこれらのオブジェクトとの間における衝突判定を実装しよう。
実際のプログラムは次のとおり。
[Code1] (実行結果 図21)
// ..
// 44行目までは 2-14節 Code2 と同じ
// ..
// Object Motion
T = TH2DMath.GetTranslation3x3(c_posMoon);
Moon.SetMatrix(T);
T = TH2DMath.GetTranslation3x3(c_posEllipse);
Ellipse.SetMatrix(T);
T = TH2DMath.GetTranslation3x3(c_posStar);
Star.SetMatrix(T);
T = TH2DMath.GetTranslation3x3(c_posLetter);
Letter.SetMatrix(T);
// Collision Test
Vector2 shell_pos = OneShell.GetPosition();
foreach(var obj in i_collisionObjects)
{
THMatrix3x3 mtx = obj.GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos);
bool bColl = CollisionTest_Point_TriMesh(P, obj.initTriangleCoords);
if (bColl)
{
Hit(obj);
break;
}
}

47行目から57行目で 4つのオブジェクトを適当な位置に配置している。ここで使われている c_posMoon、c_posEllipse、c_posStar、c_posLetter はそれぞれのオブジェクトが配置される位置を表す Vector2型の定数である。
59行目以降が衝突判定処理である。今回は衝突判定の対象となるオブジェクトが4つであるため、62行目の foreachループ内でその1つ1つと、Shellが衝突したかどうかを調べている。62行目の i_collisionObjects は衝突判定の対象となる4つのオブジェクトがセットされている配列(インスタンス変数)であり、以下のようにセットされている。衝突判定はオブジェクトが複数になったために foreach文が使われているが、その内容は本節の解説で見てきたものと特に変わるところはない。
// 衝突判定対象となるオブジェクト
i_collisionObjects = new THAlphaObject2D[] { Moon, Ellipse, Star, Letter };
# Code2
Code1では4つのオブジェクトは静止したままであったが、今回はオブジェクトが指定の位置において回転をしている。その状況においての衝突判定を行うが、オブジェクトが運動をしている場合であっても、衝突判定のコード自体は何ら変わることはない。[Code2] (実行結果 図22)
// ..
// 44行目までは 2-14節 Code2 と同じ
// ..
// Object Motion
i_deg += 1.0f;
R = TH2DMath.GetRotation3x3(i_deg);
T = TH2DMath.GetTranslation3x3(c_posMoon);
M = T * R;
Moon.SetMatrix(M);
T = TH2DMath.GetTranslation3x3(c_posEllipse);
M = T * R;
Ellipse.SetMatrix(M);
T = TH2DMath.GetTranslation3x3(c_posStar);
M = T * R;
Star.SetMatrix(M);
T = TH2DMath.GetTranslation3x3(c_posLetter);
M = T * R;
Letter.SetMatrix(M);
// Collision Test
Vector2 shell_pos = OneShell.GetPosition();
foreach(var obj in i_collisionObjects)
{
THMatrix3x3 mtx = obj.GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos);
bool bColl = CollisionTest_Point_TriMesh(P, obj.initTriangleCoords);
if (bColl)
{
Hit(obj);
break;
}
}

オブジェクトが静止していても運動をしていても、そのオブジェクトに実行されている逆行列によって、オブジェクトを初期状態に戻した状態で衝突判定を行うという処理は変わらない。ただし繰り返しになるが、実際にオブジェクトの逆行列が使われるのは、オブジェクトを初期状態に戻した際のShellの位置を求めるときのみである (プログラム72行目)。
なお、1点追記しておこう。
本節で使われたMoonやStarは、以下の図に示されるように先の尖った部分を持っている。こういったオブジェクトについては、場合によっては本節の方法では衝突が検出されないことがある。言い換えれば、オブジェクトが細い部分を持っている場合には、そういったオブジェクトの衝突判定には注意が必要である。


以下では Starを例にとって話を進める。

本節で解説した三角形との衝突判定や、2-13節で解説した円盤及び長方形との衝突判定のアルゴリズムはいわゆる内外判定に属すものである。内外判定とは、ある点がオブジェクトに含まれていれば衝突として扱うが、含まれていない場合には衝突とはみなさない。衝突の判定方法がこのような基準であると、次のようなケースでは衝突は検出されなくなる。以下に示す例は図25のアニメーションのある時点での様子である。


図26は Planeから発射されたShellが、ある時点において図に示される位置$P$に進んだときのものである。ここでは、Shellの進行速度が1フレーム当たり $0.5$ であるとする。図27は図26からちょうど1フレーム後の様子であり、そのときの Shellの位置を $P'$ とする。図26から1フレーム経過したときのものなので図27の Shellの位置$P'$は図26の位置$P$から $0.5$ だけ離れているわけである。

しかし、図25のアニメーションでは Shellは Starに衝突しているように見える。これは、フレームを連続的に表示したときにそう見えているだけで、フレームを1枚1枚見ていくと あるフレームにおいて Starの上部付近で Shellが位置$P$まで進んだとき、その次のフレームで Shellは位置$P'$に進んでいるのである。Shellがこのような進み方をする場合、フレームを連続的に表示したもの(図25のアニメーション)を見る限りでは衝突しているように見えるが、実際には Shellはその進行中に Starの近傍に来ることはあっても、Starに含まれることはないのである。このような理由で、図25では衝突が検出されていないのである。
つまり、オブジェクトのある部分がとても細く、Shellの1フレームあたりの移動距離よりも小さいときには、Shellがオブジェクトのその部分の近傍に進み、その次の移動で Shellがその部分を通り越した位置に移動することが起こり得るわけである。このような場合には、内外判定では衝突は検出されずに、Shellは何事なくオブジェクト上を通過していってしまう。
最後に一点。
本節のプログラムでは、Plane及び Shellの運動に関する記述は 2-14節のCode2と同じものであった。以降の衝突判定のプログラムにおいても、それは同様であるので、2-14節 Code2における Planeの運動に関する部分を UserMotion() という名前のメソッドとして以下のように独立させる。
[UserMotion()]
void UserMotion()
{
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Vector2 curP = Plane.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.20f * forwardDir : curP;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Plane.SetMatrix(M);
}
プログラムの記述量が増えてきたため、同じような記述はメソッド化してプログラムの可読性を保持していくための便宜的な措置である。
© 2020-2025 Redpoll's 60 (All rights reserved)