Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-19
第2章 2D空間におけるオブジェクトの運動
$§$2-19 衝突判定 6 (軸平行な長方形同士の衝突)
本節から2-21節までは円盤や長方形のような単純形状のオブジェクトを用いて、オブジェクト同士の衝突判定について見ていく。
2-17節までに扱ってきた衝突判定は、点を表すShellというオブジェクトが他のオブジェクトに含まれているかどうかを調べる、いわゆる内外判定であった。オブジェクト同士の衝突判定は、2つのオブジェクトの間に重なりがあるかを調べることによって行われる。つまり、2つのオブジェクトの間に重なりがあれば、その2つのオブジェクトは衝突しているものとみなされる。
以下の図1は2つの円盤が重なっている状態、すなわち2つの円盤が衝突しているときの状態であり、図2は2つの円盤が衝突していないときの状態である。
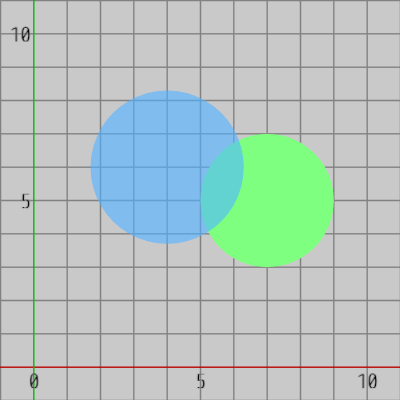
図1 2つの円盤が衝突している状態 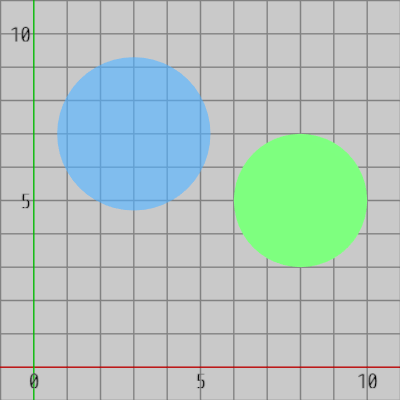
図2 2つの円盤が衝突していない状態
一方の円盤の中心を $C_1$、半径を $r_1$ とし、もう一方の円盤の中心を $C_2$、半径を $r_2$ とする。そして、2つの円盤の中心 $C_1$ と $C_2$ の間の距離を $l$ とする。
このとき、以下の条件が満たされるならば2つの円盤は重なっている状態であり、すなわち衝突している。
\[ r_1 + r_2\ \geq\ l \]
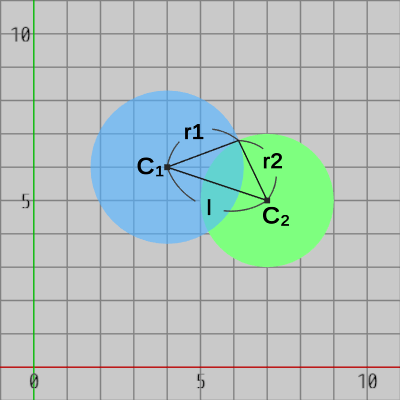
図3 r1 + r2 >= l 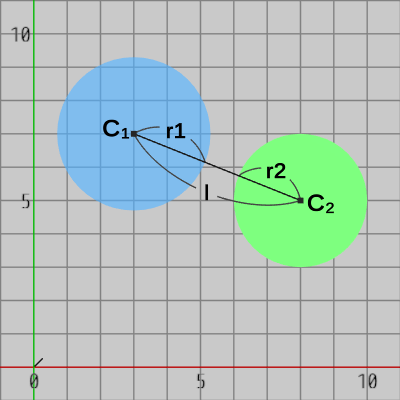
図4 r1 + r2 < l
図3は2つの円盤が衝突している状態であるが、確かに $r_1 + r_2 \geq l$ である。
図4は衝突していない状態であり、この場合は明らかに $r_1 + r_2 < l$ である。
以下の CollisionTest_Disk_Disk(..) は、今述べてきたことをメソッドにしたものである。
[CollisionTest_Disk_Disk(..)]
なお、軸平行な長方形や直方体は「AABB (Axis Aligned Bounding Box)」という略称で表記されることが多いが、ここでもそれを使用する。
1-3節で既に見てきたが、ある点からある直線上へ垂線を下すことを「直交する方向への射影」(詳しくは「正射影」)というのであった。以下では「直交する方向」と書かれていなくても「射影」といえば「直交する方向への射影」を意味するものとする。図5は点$P$から直線$l$への射影を表している。
射影に関連して1つの用語を定義する。
ある図形をある直線上に、その直線に対して直交する方向に射影したときにできる領域のことを 射影区間 と定義する (ここで扱う図形は’単純な’もののみであり、途切れているとか穴が開いている、あるいは無限の大きさであるとか開集合といった面倒な場合はもちろん除外する)。
図6は(軸平行な)長方形の各頂点を x軸上に射影したときのものであるが、このときの像(射影された点)の最小値と最大値の間の範囲がこの長方形の射影区間であり、射影区間は x軸上の $2$ から $8$ である (青い太線の範囲)。
また、図7は黒い直線上へ長方形を射影したときのものであるが、このときの射影区間は $P$ から $Q$ である (緑色の太線の範囲)。
以下に示されるように、凹型の図形であっても射影区間は存在する。

図8 射影区間はAからB 
図9 射影区間はCからD
図8は青い図形を x軸上に射影したときのものであるが、射影区間は x軸上の $A$ から $B$である (青い図形の各頂点をx軸上に射影したときの最小値と最大値が$A$と$B$)。また、図9は緑の図形を黒い直線上に射影したときのものであるが、射影区間は黒い直線上の $C$ から $D$ である。
下図には2つの軸平行な長方形が衝突した状態で置かれている。
図11はこの2つの長方形を x軸上に射影したときのものであり、図12は2つの長方形を y軸上に射影したときのものである。
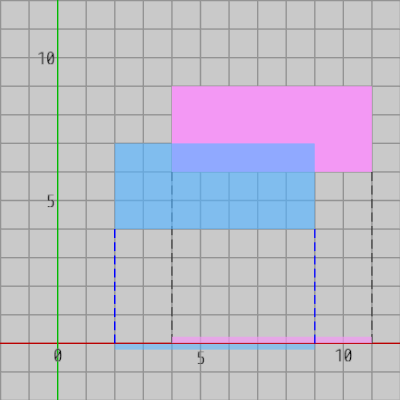
図10 x軸上へ射影(2つの射影区間は4から9の間で重なっている) 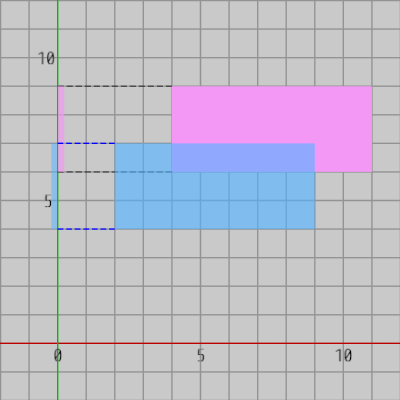
図11 y軸上へ射影(2つの射影区間は6から7の間で重なっている)
図10から分かるように x軸上に射影したときの2つの長方形の射影区間は重なっている状態である ($4$から$9$の範囲が重なっている)。同様に図11における y軸上の両者の射影区間も重なっている状態である ($6$から$7$の範囲が重なっている)。
つまり、2つの軸平行な長方形が衝突している場合、その2つの長方形を x軸上に射影したとき、及び y軸上に射影したときの両者の射影区間には重なりが生じるのである。
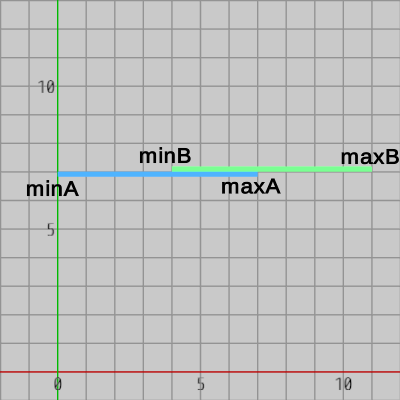
図12 2つの線分の重なり 右図は2つの線分が重なっている状態を示している。青い線分を $A$、緑色の線分を $B$ とし、2つの線分の最小値、最大値をそれぞれ $minA$、$maxA$、$minB$、$maxB$ とする。 2つの線分に重なりがあることを数式で表すと以下のようになる (以下の $\&\&$ はプログラム言語における論理積と同じ意味である)。
\[ minA < maxB\ \ \&\&\ \ minB < maxA \]
2つの軸平行な長方形が重なっているときには、x軸上の2つの射影区間も重なっており、さらに y軸上の2つの射影区間も重なっている。
先程の2つの長方形を $A$、$B$ とし、それぞれの x軸、y軸上の射影区間の最小値、最大値をそれぞれ $minA.x$、$maxA.x$、$minA.y$、$maxA.y$、$minB.x$、$maxB.x$、$minB.y$、$maxB.y$ とすると、それらは以下の図のように示される。
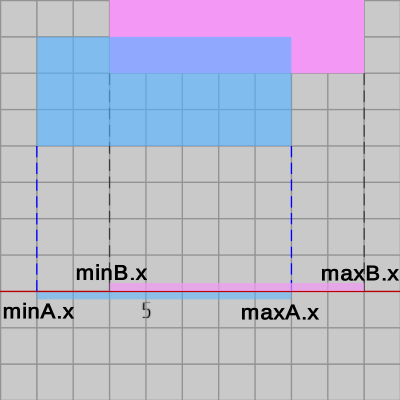
図13 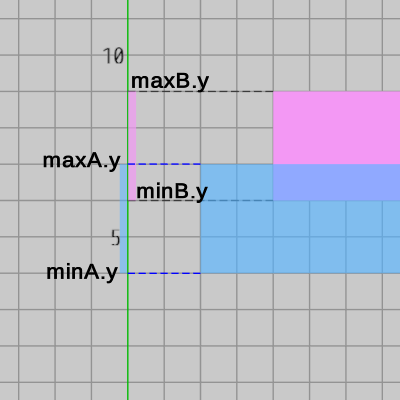
図14
x軸上の2つの射影区間が重なっていることは、次の条件式が成り立つことを意味する。\[ minA.x < maxB.x\ \ \&\&\ \ minB.x < maxA.x \]同様に、y軸上の2つの射影区間が重なっていることは、次の条件式が成り立つことを意味する。\[ minA.y < maxB.y\ \ \&\&\ \ minB.y < maxA.y \]したがって、x軸上の2つの射影区間 及び y軸上の2つの射影区間が重なっていることは上記のx軸とy軸の条件式の両方が成り立つことを意味する。
以下の CollisionTest_AABB_AABB(..) は軸平行な長方形同士が衝突しているかどうかを判定するメソッドであり、今述べてきたことを実装したものである。
[CollisionTest_AABB_AABB(..)]
メソッドの引数には2つの軸平行な長方形$A$、$B$の左下隅、右上隅の頂点座標が送られてくる (minA、maxAは長方形$A$の左下隅、右上隅を表している)。
軸平行な長方形の場合には x軸上の射影区間の最小値、y軸上の射影区間の最小値は その長方形の左下隅頂点の x座標、y座標に等しい。また、x軸上の射影区間の最大値、y軸上の射影区間の最大値は その長方形の右上隅頂点の x座標、y座標に等しい。
ここで、衝突判定において重要な概念を導入するために以下では軸平行な長方形同士が衝突していない場合について見ていくことにする。
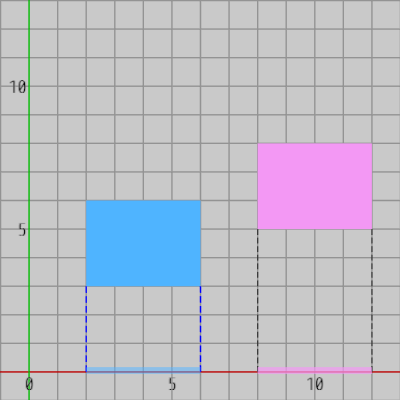
図15 x軸上への射影(2つの射影区間の間に間隔が存在する) 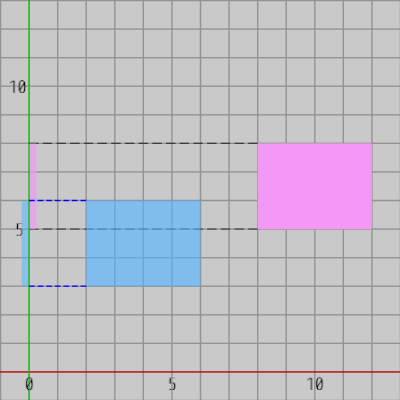
図16 y軸上への射影(2つの射影区間は重なっている)
上の2つの図には、2つの軸平行な長方形が重なっていない状態(衝突していない状態)で置かれている。図15はその2つの長方形を x軸上に射影したときのものであり、図16は両者を y軸上に射影したときのものである。図16のy軸上の2つの射影区間は重なっているが、図15のx軸上の2つの射影区間には重なりが見られず、x軸上の2つの射影区間の間には間隔が存在している。

図17 分離軸と分離直線 図15に見られるように、2つの図形をある直線上に射影したときに、2つの射影区間の間に間隔が存在する場合(2つの射影区間が分離している場合)、この直線のことを分離軸(separating axis)という。したがって 図15のx軸は分離軸であるが、図16のy軸は2つの射影区間の間に間隔が存在しないので分離軸ではない。
また、便宜上 分離軸上の2つの射影区間の間に存在する間隔を以降 ギャップ(gap) と呼ぶことにする。
分離軸上のギャップを通り、分離軸に直交する直線は明らかに2つの図形とは交わらない。この直線のことを分離直線という (図17)。
長方形同士の衝突判定は、この分離軸を使って以下のうちどちらが該当するかを調べることに帰着する (長方形は傾きがあっても構わない)。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
しかし、一番重要な問題である「どのような直線が分離軸となるのか」についてはまだ解決されていない。
上で扱ったように、2つの長方形が x軸、y軸に平行であれば分離軸は x軸か y軸である。したがって、この2つの軸に関して射影区間の比較を行えばよい。しかし、どちらかの長方形に傾きがある場合は単純にx軸、y軸を比較するだけでは正しい結果になるとは限らない。
この問題については、傾きのある長方形同士の衝突を扱う 2-21節において解説する。
しかし「ある直線が分離軸になる」ならば、なぜ「2つの長方形は重なっていない」ことがいえるのか、あるいは「どのような直線も分離軸にならない」ならば、なぜ「2つの長方形は重なっている」ことがいえるのかについては上記では触れてはいない。
以下ではこの点について若干の数学的な補足をする。
(以下の内容は長方形同士の衝突判定プログラムを作成する際に必須というわけではないので、特に興味がなければとばしても構わない)

図18 白い領域には2つの図形は含まれない(白い領域はギャップと直交している) まず、分離軸と分離直線については一方が存在するならば必ずもう一方も存在することに注意しておこう。
実際、分離軸が存在するとき分離軸上の2つの射影区間の間にはギャップが存在することになるが、このとき 図18に示されるようなギャップと直交する白い領域にはどちらの図形も含まれていない。したがって、この白い領域から外に出ないような直線は2つの図形と交わることのない直線であるから、この領域内に分離軸と直交する直線を引けばそれが分離直線である。
逆に2つの図形の間に分離直線を引けるならば、明らかにその直線の近傍にその直線に平行な領域、図18に示されるような白い領域が存在する。
そして、分離直線上の任意の位置において分離直線に直交する直線を引くことができるが、その直線もまたその白い領域を含んでいる。2つの図形は白い領域を挟んで両側に置かれているため、2つの図形を 分離直線に直交するその直線に射影したときには、2つの射影区間もまた白い領域を挟んで両側に位置することになる。
これはこの直線上にギャップが存在することを意味するから、この直線が分離軸になる。
すなわち、分離軸が存在するならば分離直線も存在し、分離直線が存在するならば分離軸も存在するのである (分離軸と分離直線の同値性は図形に依存しない。ここでは長方形を対象としているが、通常の凸図形、凹図形でも一方が存在するならばもう一方も存在する)。
以下、上記の2つの命題について簡単に補足する。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
この命題はほとんど明らかである。今述べたように、分離軸が存在するならば分離直線が存在するので2つの長方形は重なっていない (この命題は長方形でなくても通常の凸図形、凹図形でも成り立つ)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
ある命題を考えることは、その命題の対偶を考ても同じである。(2)の対偶は「2つの長方形が重なっていないならば、ある直線が分離軸になる」である。これは(1)の逆であるが、この命題は成り立つ。詳しくは、2-21節で解説するが長方形の場合には、2つの長方形が重なっていなければそれらの間に分離直線が存在するのである(それは分離軸が存在することを意味する)。
つまり、(2)の待遇が成り立つので(2)も成り立つ。
また これも2-21節で解説するが、2つの長方形が重なっていないならば、2つの長方形のうちのある辺に平行な直線は必ず分離直線になる。この場合、2つの長方形のうちのある辺に平行な直線は必ず分離軸になる (分離直線と分離軸は直交しており、さらに長方形の各辺も直交しているので)。
言い換えれば、2つの長方形の各辺に平行な直線がいずれも分離軸にならないならば、2つの長方形は重なっているということである。
したがって 長方形同士の衝突判定では、2つの長方形の各辺に平行な直線上において両者の射影区間の比較を行えばよいわけである。長方形は2組の平行な辺によって構成されているので「2つの長方形の各辺に平行な直線」は多くて4つである。この4つの直線が分離軸の候補となる直線であり、このいずれもが分離軸にならないのであれば2つの長方形は重なっているのである。
では最後に、本節で述べた内容に関するプログラムを作成する。
以下のプログラムを実行すると緑の円盤が適当な運動をおこなっている。青い円盤はキー操作によって動かすことができ、両者が衝突すると両者は赤い色に変わる。
青い円盤を動かすためのキー操作は次のとおり。
H : 左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
また、Sキーによって緑の円盤の運動を 停止/再開 させることができる。
[Code1] (実行結果 図20)
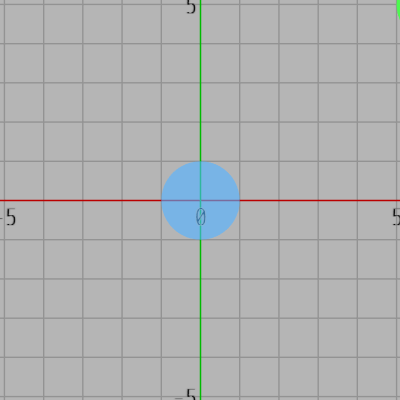
図19 円盤の半径は 1 
図20 Code1 実行結果
プログラム中の Blue、Green は青い円盤、緑の円盤を表す変数である。
1行目のifブロックは初期化ブロックであり、i_radBlue、i_radGreen は2つの円盤の半径を表すインスタンス変数で、今回は両方とも半径は $1$ である (図19)。i_MOVE は Greenの運動のためのスイッチ用のインスタンス変数であり、初期値は true である。このインスタンス変数は、Sキーが押されるたびに11行目のifブロックで値が変わるが、true のときに Greenは運動を行い、false のときには停止している。Greenの運動は18行目で呼ばれるメソッド GreenMotion(..) に記述されている。このメソッドの引数が $0$ のときは単振動、$1$ のときは原点周りの公転運動である。GreenMotion(..) の内容自体は単純なものであり、ここでは特に重要ではないので解説は省略する。
21行目から42行目はキー操作によってBlueを動かす部分である。Blueの現在位置を取得し(21行目)、キーを押した方向に $0.1$ だけ移動させる。
45行目において円盤同士の衝突判定用のメソッド CollisionTest_Disk_Disk(..) を実行している。
このメソッドは上で見たように、引数には2つの円盤の中心位置及び半径をセットするが、ここではBlueの中心位置(posB)、半径(i_radBlue)、Greenの中心位置(posG)、半径(i_radGreen) がセットされている。
このメソッドの結果は bool型で返されるが、その結果を46行目のメソッド Hit(..) にセットすると 衝突していれば自動的に両者は赤い色に変化する。
プログラムを実行すると緑の長方形が適当な運動を行っている。青い長方形はキー操作によって動かすことができ、両者が衝突すると両者は赤い色に変わる。
ここでのキー操作は前回と同様である。
H : (青い長方形を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
S : 緑の長方形の運動の停止/再開
また、Code1と同様に緑の長方形、青い長方形はそれぞれプログラムでは Green、Blue として使われている。
[Code2] (実行結果 図22)
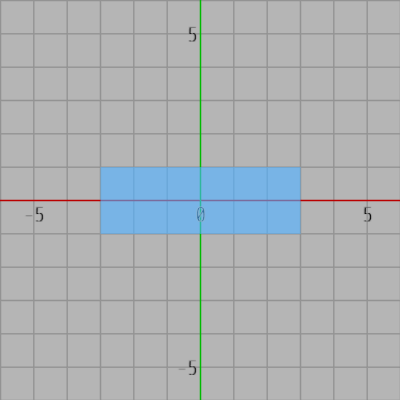
図21 長方形のサイズ 6x2 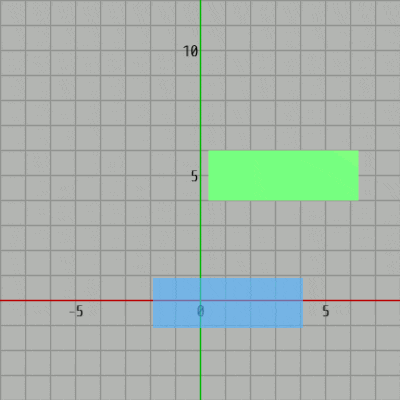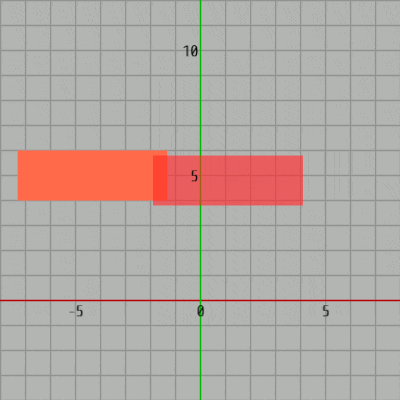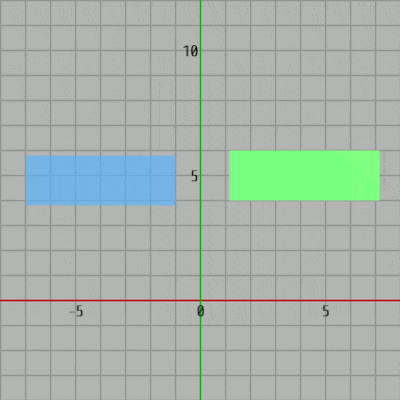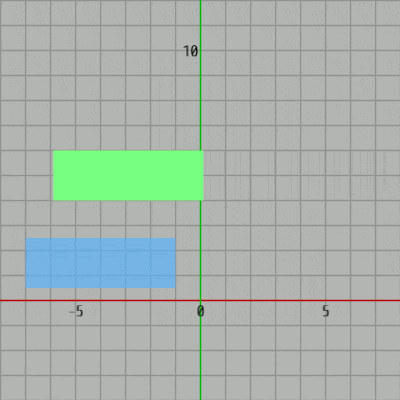
図22 Code2 実行結果
このプログラムで使われている長方形は2つとも同じ大きさであり、横の長さ $6$、縦の長さ $2$ である。また、初期状態においては左下隅、右上隅の頂点の座標は $(-3, -1)$、$(3,\ 1)$ である (図21)。以下、便宜上 長方形の左下隅の頂点を min、右上隅の頂点を max と表記する。
1行目のifブロックは初期化ブロックであり、インスタンス変数 i_initMinMaxGreen、i_initMinMaxBlue にはそれぞれ Green、Blue の初期状態における min、max をセットしている ([0]にmin、[1]にmaxをセットする)。
11行目から42行目は、Code1と全く同じであり Greenの運動の停止/再開やBlueをキー操作によって動かす部分である。18行目の GreenMotion(..) もCode1と同様に、引数が $0$ であればGreenは単振動を行い、$1$ であれば原点周りの公転を行う。
45行目から48行目では、その時点における Green、Blueの min、max を求めている。posG、posB はその時点での Green、Blueの位置(長方形の中心座標)を表すが、この値はそれぞれの長方形が初期状態からどれだけ移動したかを表すものである。i_initMinMaxGreen、i_initMinMaxBlue には初期状態での Green、Blueの min、max がセットされているので、これに posG、posB を加算すればその時点での Green、Blue の min、max が求められるわけである。
50行目の CollisionTest_AABB_AABB(..) は上で解説した軸平行な長方形同士の衝突判定用メソッドであり、両者が衝突していればtrueを返す。その下の Hit(..) はCode1と役割は同じであり、2つの長方形が衝突していれば両者を赤く表示する。
2-17節までに扱ってきた衝突判定は、点を表すShellというオブジェクトが他のオブジェクトに含まれているかどうかを調べる、いわゆる内外判定であった。オブジェクト同士の衝突判定は、2つのオブジェクトの間に重なりがあるかを調べることによって行われる。つまり、2つのオブジェクトの間に重なりがあれば、その2つのオブジェクトは衝突しているものとみなされる。
A) 円盤 対 円盤 (Disk vs Disk)
最も単純なケースである。以下の図1は2つの円盤が重なっている状態、すなわち2つの円盤が衝突しているときの状態であり、図2は2つの円盤が衝突していないときの状態である。


一方の円盤の中心を $C_1$、半径を $r_1$ とし、もう一方の円盤の中心を $C_2$、半径を $r_2$ とする。そして、2つの円盤の中心 $C_1$ と $C_2$ の間の距離を $l$ とする。
このとき、以下の条件が満たされるならば2つの円盤は重なっている状態であり、すなわち衝突している。
\[ r_1 + r_2\ \geq\ l \]


図3は2つの円盤が衝突している状態であるが、確かに $r_1 + r_2 \geq l$ である。
図4は衝突していない状態であり、この場合は明らかに $r_1 + r_2 < l$ である。
以下の CollisionTest_Disk_Disk(..) は、今述べてきたことをメソッドにしたものである。
[CollisionTest_Disk_Disk(..)]
// Disk vs Disk
bool CollisionTest_Disk_Disk(Vector2 C1, float r1, Vector2 C2, float r2)
{
float l = (C1 - C2).magnitude;
if(r1 + r2 >= l)
{
return true;
}
return false;
}
B) 軸平行な長方形 対 軸平行な長方形 (AABB vs AABB)
次に各辺が x軸、y軸に平行な長方形、すなわち軸平行な長方形同士の衝突判定について考える。なお、軸平行な長方形や直方体は「AABB (Axis Aligned Bounding Box)」という略称で表記されることが多いが、ここでもそれを使用する。
1-3節で既に見てきたが、ある点からある直線上へ垂線を下すことを「直交する方向への射影」(詳しくは「正射影」)というのであった。以下では「直交する方向」と書かれていなくても「射影」といえば「直交する方向への射影」を意味するものとする。図5は点$P$から直線$l$への射影を表している。
-
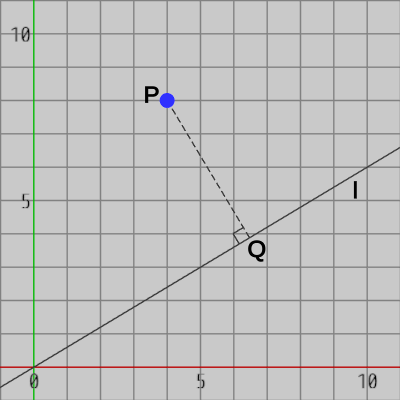 図5 点Pから直線 l への射影
図5 点Pから直線 l への射影 -
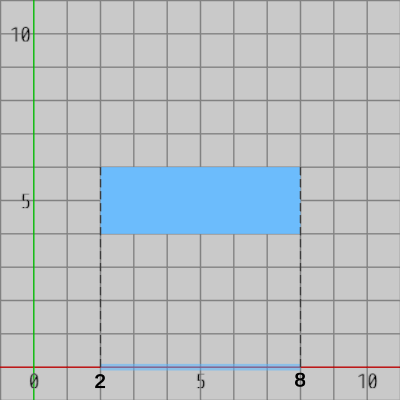 図6 長方形(の各頂点)をx軸上へ射影
図6 長方形(の各頂点)をx軸上へ射影 -
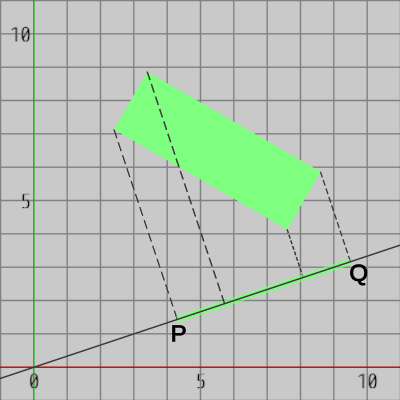 図7 長方形(の各頂点)を黒い直線上へ射影
図7 長方形(の各頂点)を黒い直線上へ射影
射影に関連して1つの用語を定義する。
ある図形をある直線上に、その直線に対して直交する方向に射影したときにできる領域のことを 射影区間 と定義する (ここで扱う図形は’単純な’もののみであり、途切れているとか穴が開いている、あるいは無限の大きさであるとか開集合といった面倒な場合はもちろん除外する)。
図6は(軸平行な)長方形の各頂点を x軸上に射影したときのものであるが、このときの像(射影された点)の最小値と最大値の間の範囲がこの長方形の射影区間であり、射影区間は x軸上の $2$ から $8$ である (青い太線の範囲)。
また、図7は黒い直線上へ長方形を射影したときのものであるが、このときの射影区間は $P$ から $Q$ である (緑色の太線の範囲)。
以下に示されるように、凹型の図形であっても射影区間は存在する。


図8は青い図形を x軸上に射影したときのものであるが、射影区間は x軸上の $A$ から $B$である (青い図形の各頂点をx軸上に射影したときの最小値と最大値が$A$と$B$)。また、図9は緑の図形を黒い直線上に射影したときのものであるが、射影区間は黒い直線上の $C$ から $D$ である。
下図には2つの軸平行な長方形が衝突した状態で置かれている。
図11はこの2つの長方形を x軸上に射影したときのものであり、図12は2つの長方形を y軸上に射影したときのものである。


図10から分かるように x軸上に射影したときの2つの長方形の射影区間は重なっている状態である ($4$から$9$の範囲が重なっている)。同様に図11における y軸上の両者の射影区間も重なっている状態である ($6$から$7$の範囲が重なっている)。
つまり、2つの軸平行な長方形が衝突している場合、その2つの長方形を x軸上に射影したとき、及び y軸上に射影したときの両者の射影区間には重なりが生じるのである。

\[ minA < maxB\ \ \&\&\ \ minB < maxA \]
2つの軸平行な長方形が重なっているときには、x軸上の2つの射影区間も重なっており、さらに y軸上の2つの射影区間も重なっている。
先程の2つの長方形を $A$、$B$ とし、それぞれの x軸、y軸上の射影区間の最小値、最大値をそれぞれ $minA.x$、$maxA.x$、$minA.y$、$maxA.y$、$minB.x$、$maxB.x$、$minB.y$、$maxB.y$ とすると、それらは以下の図のように示される。

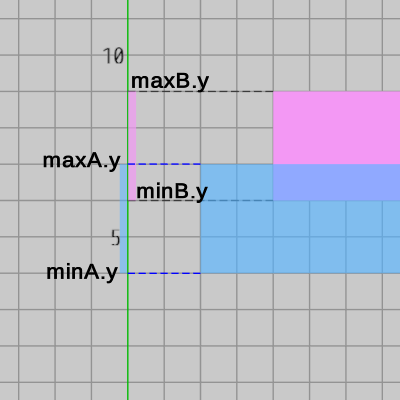
x軸上の2つの射影区間が重なっていることは、次の条件式が成り立つことを意味する。\[ minA.x < maxB.x\ \ \&\&\ \ minB.x < maxA.x \]同様に、y軸上の2つの射影区間が重なっていることは、次の条件式が成り立つことを意味する。\[ minA.y < maxB.y\ \ \&\&\ \ minB.y < maxA.y \]したがって、x軸上の2つの射影区間 及び y軸上の2つの射影区間が重なっていることは上記のx軸とy軸の条件式の両方が成り立つことを意味する。
以下の CollisionTest_AABB_AABB(..) は軸平行な長方形同士が衝突しているかどうかを判定するメソッドであり、今述べてきたことを実装したものである。
[CollisionTest_AABB_AABB(..)]
// AABB vs AABB
bool CollisionTest_AABB_AABB(Vector2 minA, Vector2 maxA, Vector2 minB, Vector2 maxB)
{
if(minA.x < maxB.x && minA.y < maxB.y &&
minB.x < maxA.x && minB.y < maxA.y)
{
return true;
}
return false;
}
メソッドの引数には2つの軸平行な長方形$A$、$B$の左下隅、右上隅の頂点座標が送られてくる (minA、maxAは長方形$A$の左下隅、右上隅を表している)。
軸平行な長方形の場合には x軸上の射影区間の最小値、y軸上の射影区間の最小値は その長方形の左下隅頂点の x座標、y座標に等しい。また、x軸上の射影区間の最大値、y軸上の射影区間の最大値は その長方形の右上隅頂点の x座標、y座標に等しい。
ここで、衝突判定において重要な概念を導入するために以下では軸平行な長方形同士が衝突していない場合について見ていくことにする。


上の2つの図には、2つの軸平行な長方形が重なっていない状態(衝突していない状態)で置かれている。図15はその2つの長方形を x軸上に射影したときのものであり、図16は両者を y軸上に射影したときのものである。図16のy軸上の2つの射影区間は重なっているが、図15のx軸上の2つの射影区間には重なりが見られず、x軸上の2つの射影区間の間には間隔が存在している。

また、便宜上 分離軸上の2つの射影区間の間に存在する間隔を以降 ギャップ(gap) と呼ぶことにする。
分離軸上のギャップを通り、分離軸に直交する直線は明らかに2つの図形とは交わらない。この直線のことを分離直線という (図17)。
長方形同士の衝突判定は、この分離軸を使って以下のうちどちらが該当するかを調べることに帰着する (長方形は傾きがあっても構わない)。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
しかし、一番重要な問題である「どのような直線が分離軸となるのか」についてはまだ解決されていない。
上で扱ったように、2つの長方形が x軸、y軸に平行であれば分離軸は x軸か y軸である。したがって、この2つの軸に関して射影区間の比較を行えばよい。しかし、どちらかの長方形に傾きがある場合は単純にx軸、y軸を比較するだけでは正しい結果になるとは限らない。
この問題については、傾きのある長方形同士の衝突を扱う 2-21節において解説する。
C) 分離軸判定に関する数学的背景
上で述べたように、2つの長方形の衝突判定は分離軸を使って「ある直線が分離軸になるか」あるいは「どのような直線も分離軸にならないか」を調べることによって行われる。しかし「ある直線が分離軸になる」ならば、なぜ「2つの長方形は重なっていない」ことがいえるのか、あるいは「どのような直線も分離軸にならない」ならば、なぜ「2つの長方形は重なっている」ことがいえるのかについては上記では触れてはいない。
以下ではこの点について若干の数学的な補足をする。
(以下の内容は長方形同士の衝突判定プログラムを作成する際に必須というわけではないので、特に興味がなければとばしても構わない)

実際、分離軸が存在するとき分離軸上の2つの射影区間の間にはギャップが存在することになるが、このとき 図18に示されるようなギャップと直交する白い領域にはどちらの図形も含まれていない。したがって、この白い領域から外に出ないような直線は2つの図形と交わることのない直線であるから、この領域内に分離軸と直交する直線を引けばそれが分離直線である。
逆に2つの図形の間に分離直線を引けるならば、明らかにその直線の近傍にその直線に平行な領域、図18に示されるような白い領域が存在する。
そして、分離直線上の任意の位置において分離直線に直交する直線を引くことができるが、その直線もまたその白い領域を含んでいる。2つの図形は白い領域を挟んで両側に置かれているため、2つの図形を 分離直線に直交するその直線に射影したときには、2つの射影区間もまた白い領域を挟んで両側に位置することになる。
これはこの直線上にギャップが存在することを意味するから、この直線が分離軸になる。
すなわち、分離軸が存在するならば分離直線も存在し、分離直線が存在するならば分離軸も存在するのである (分離軸と分離直線の同値性は図形に依存しない。ここでは長方形を対象としているが、通常の凸図形、凹図形でも一方が存在するならばもう一方も存在する)。
以下、上記の2つの命題について簡単に補足する。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
この命題はほとんど明らかである。今述べたように、分離軸が存在するならば分離直線が存在するので2つの長方形は重なっていない (この命題は長方形でなくても通常の凸図形、凹図形でも成り立つ)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
ある命題を考えることは、その命題の対偶を考ても同じである。(2)の対偶は「2つの長方形が重なっていないならば、ある直線が分離軸になる」である。これは(1)の逆であるが、この命題は成り立つ。詳しくは、2-21節で解説するが長方形の場合には、2つの長方形が重なっていなければそれらの間に分離直線が存在するのである(それは分離軸が存在することを意味する)。
つまり、(2)の待遇が成り立つので(2)も成り立つ。
また これも2-21節で解説するが、2つの長方形が重なっていないならば、2つの長方形のうちのある辺に平行な直線は必ず分離直線になる。この場合、2つの長方形のうちのある辺に平行な直線は必ず分離軸になる (分離直線と分離軸は直交しており、さらに長方形の各辺も直交しているので)。
言い換えれば、2つの長方形の各辺に平行な直線がいずれも分離軸にならないならば、2つの長方形は重なっているということである。
したがって 長方形同士の衝突判定では、2つの長方形の各辺に平行な直線上において両者の射影区間の比較を行えばよいわけである。長方形は2組の平行な辺によって構成されているので「2つの長方形の各辺に平行な直線」は多くて4つである。この4つの直線が分離軸の候補となる直線であり、このいずれもが分離軸にならないのであれば2つの長方形は重なっているのである。
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
第1のプログラムは円盤同士の衝突判定である。以下のプログラムを実行すると緑の円盤が適当な運動をおこなっている。青い円盤はキー操作によって動かすことができ、両者が衝突すると両者は赤い色に変わる。
青い円盤を動かすためのキー操作は次のとおり。
H : 左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
また、Sキーによって緑の円盤の運動を 停止/再開 させることができる。
[Code1] (実行結果 図20)
if (!i_INITIALIZED)
{
i_radBlue = 1.0f;
i_radGreen = 1.0f;
i_MOVE = true;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S)) // Greenの運動の停止/再開
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
GreenMotion(1); // Greenの運動 (0 単振動 ; 1 公転)
}
Vector2 posB = Blue.GetPosition();
float speed = 0.10f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
Blue.SetPosition(posB);
Vector2 posG = Green.GetPosition();
bool bColl = CollisionTest_Disk_Disk(posB, i_radBlue, posG, i_radGreen);
Hit(bColl);


プログラム中の Blue、Green は青い円盤、緑の円盤を表す変数である。
1行目のifブロックは初期化ブロックであり、i_radBlue、i_radGreen は2つの円盤の半径を表すインスタンス変数で、今回は両方とも半径は $1$ である (図19)。i_MOVE は Greenの運動のためのスイッチ用のインスタンス変数であり、初期値は true である。このインスタンス変数は、Sキーが押されるたびに11行目のifブロックで値が変わるが、true のときに Greenは運動を行い、false のときには停止している。Greenの運動は18行目で呼ばれるメソッド GreenMotion(..) に記述されている。このメソッドの引数が $0$ のときは単振動、$1$ のときは原点周りの公転運動である。GreenMotion(..) の内容自体は単純なものであり、ここでは特に重要ではないので解説は省略する。
21行目から42行目はキー操作によってBlueを動かす部分である。Blueの現在位置を取得し(21行目)、キーを押した方向に $0.1$ だけ移動させる。
45行目において円盤同士の衝突判定用のメソッド CollisionTest_Disk_Disk(..) を実行している。
このメソッドは上で見たように、引数には2つの円盤の中心位置及び半径をセットするが、ここではBlueの中心位置(posB)、半径(i_radBlue)、Greenの中心位置(posG)、半径(i_radGreen) がセットされている。
このメソッドの結果は bool型で返されるが、その結果を46行目のメソッド Hit(..) にセットすると 衝突していれば自動的に両者は赤い色に変化する。
# Code2
次のプログラムは軸平行な長方形同士の衝突であるが、使用するオブジェクトが円盤から長方形に変わっただけで、その内容については先程のCode1と変わらない。プログラムを実行すると緑の長方形が適当な運動を行っている。青い長方形はキー操作によって動かすことができ、両者が衝突すると両者は赤い色に変わる。
ここでのキー操作は前回と同様である。
H : (青い長方形を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
S : 緑の長方形の運動の停止/再開
また、Code1と同様に緑の長方形、青い長方形はそれぞれプログラムでは Green、Blue として使われている。
[Code2] (実行結果 図22)
if (!i_INITIALIZED)
{
i_initMinMaxGreen = new Vector2[] { new Vector2(-3, -1), new Vector2(3, 1) };
i_initMinMaxBlue = new Vector2[] { new Vector2(-3, -1), new Vector2(3, 1) };
i_MOVE = true;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S)) // Greenの運動の停止/再開
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
GreenMotion(1); // Greenの運動 (0 単振動 ; 1 公転)
}
Vector2 posB = Blue.GetPosition();
float speed = 0.1f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
Blue.SetPosition(posB);
Vector2 posG = Green.GetPosition();
Vector2 minG = posG + i_initMinMaxGreen[0];
Vector2 maxG = posG + i_initMinMaxGreen[1];
Vector2 minB = posB + i_initMinMaxBlue[0];
Vector2 maxB = posB + i_initMinMaxBlue[1];
bool bColl = CollisionTest_AABB_AABB(minG, maxG, minB, maxB);
Hit(bColl);


このプログラムで使われている長方形は2つとも同じ大きさであり、横の長さ $6$、縦の長さ $2$ である。また、初期状態においては左下隅、右上隅の頂点の座標は $(-3, -1)$、$(3,\ 1)$ である (図21)。以下、便宜上 長方形の左下隅の頂点を min、右上隅の頂点を max と表記する。
1行目のifブロックは初期化ブロックであり、インスタンス変数 i_initMinMaxGreen、i_initMinMaxBlue にはそれぞれ Green、Blue の初期状態における min、max をセットしている ([0]にmin、[1]にmaxをセットする)。
11行目から42行目は、Code1と全く同じであり Greenの運動の停止/再開やBlueをキー操作によって動かす部分である。18行目の GreenMotion(..) もCode1と同様に、引数が $0$ であればGreenは単振動を行い、$1$ であれば原点周りの公転を行う。
45行目から48行目では、その時点における Green、Blueの min、max を求めている。posG、posB はその時点での Green、Blueの位置(長方形の中心座標)を表すが、この値はそれぞれの長方形が初期状態からどれだけ移動したかを表すものである。i_initMinMaxGreen、i_initMinMaxBlue には初期状態での Green、Blueの min、max がセットされているので、これに posG、posB を加算すればその時点での Green、Blue の min、max が求められるわけである。
50行目の CollisionTest_AABB_AABB(..) は上で解説した軸平行な長方形同士の衝突判定用メソッドであり、両者が衝突していればtrueを返す。その下の Hit(..) はCode1と役割は同じであり、2つの長方形が衝突していれば両者を赤く表示する。
© 2020-2025 Redpoll's 60 (All rights reserved)