Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-8
第2章 2D空間におけるオブジェクトの運動
$§$2-8 指定方向へのオブジェクトの移動 1
今までの節で扱ったプログラムはすべて、実行後にオブジェクトが決められた運動を繰り返し行うものであって、実行後の段階でオブジェクトを操作することはできなかった。この節からは、プログラム実行後にキー操作によってオブジェクトを操作できるようなプログラムを扱っていく。
何らかのキーを押した際には、次のメソッドがtrueを返す。
アルファベットを押したかどうかを判定するには引数の#の部分にAからZのアルファベットを指定する。キーボードの数字(テンキーではなく)を押したかどうかを判定するには#の部分にAlpha0からAlpha9を指定する。
例えば、Aを押したかどうかの判定は、とすれば、Aが押された場合にif文の中身が実行される。
キーボードの1を押したかどうかの判定は、とすれば、キーボードの1が押された場合にif文の中身が実行される。
次のプログラムはアルファベットのH、J、K、L、数字の1、2、3が押された際に該当するif文の中身が実行される(Unityのコンソール上に "PRESSED : #" と表示される)。
[Code1] (実行結果 図1)
実行結果を図1に示す。 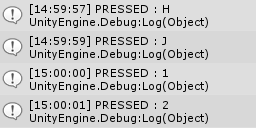
図1 Code1 実行結果
何らかのキーを押し続けている状態であるとき、次のメソッドがtrueを返す。
例えば、Aを押し続けているかどうかの判定は、とすれば、Aを押し続けている状態においてif文の中身が実行される。
次のプログラムはアルファベットのH、J、K、Lを押し続けている状態において該当するif文の中身が実行される(Unityのコンソール上に連続して "pressing : #" と表示される)。
[Code2] (実行結果 図2)
実行結果を図2に示す。 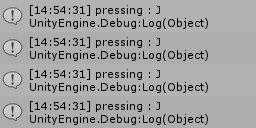
図2 Code2 実行結果
最後に、プログラム実行後から何フレーム目であるかをカウントするint型インスタンス変数 i_frameCount を使って、この2つのメソッドの動作を確認しよう (i_frameCountの初期値は $0$)。
[Beta2] (実行結果 図3)
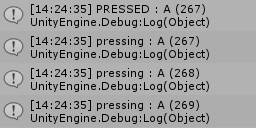
図3 Beta2 実行結果 プログラム実行後に、Aキーを押して、その後に少しの間だけ押し続けた場合の実行結果が図3である。
図では分かりずらいが、Unityのコンソール画面上の表示結果を要約すると以下のようになる。
PRESSED : A (267)
pressing : A (267)
pressing : A (268)
pressing : A (269)
... ...
pressing : A (287)
pressing : A (288)
この結果の意味することは、「プログラム実行後の267フレーム目で、Aキーが押されたことが2つのメソッドInput.GetKeyDown(..)、Input.GetKey(..)によって検出された。その後の288フレーム目までAキーは押され続けていた。」ということである。
Input.GetKeyDown(..)は押されたフレームにおいてのみtrueを返し、Input.GetKey(..)は押されたフレーム、及びその後押され続けている間のフレームにおいてtrueを返すのである。
図4は、オブジェクトPointの初期状態である。この Pointを、指定したキーを押すことによって上下左右に移動させるプログラムを作成しよう。
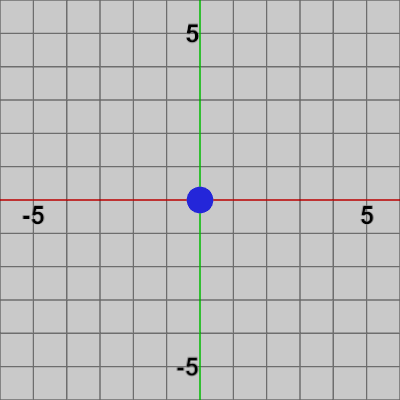
図4 Point 初期状態 
図5 Code3 実行結果
次のキー操作を実装する。
H : x軸方向に$-1$移動(左に$1$移動)
J : y軸方向に$-1$移動(下に$1$移動)
K : y軸方向に$+1$移動(上に$1$移動)
L : x軸方向に$+1$移動(右に$1$移動)
(Pointの移動量は、いずれのキーの場合でも$1$ずつの移動となる)
また、カスタムライブラリからオブジェクトの現在位置を取得するためのメソッドして次のメソッドを利用する。
このメソッドの戻り値は Vector2型で、その時点でのオブジェクトの位置座標が返される。Pointの現在位置を取得する場合は、Point.GetPosition() と記述すればよい。
手順は次の通り。
(1) Pointの現在位置を取得し、ローカル変数curPosへセット (プログラム1行目 ; Pointの初期位置は原点であるので、プログラム実行後の最初の GetPosition() の戻り値は(0, 0)である)。
(2) 押されたキーに対応する移動を curPos に加算して、現在の位置を表すデータを更新(3~18行目)。
(3) curPosだけ移動する行列を取得して、Pointに実行する(20~21行目)。
[Code3] (実行結果 図5)
20行目で算出される平行移動行列Tは、curPosだけの平行移動を行うものであるが、Pointの場合は初期状態の位置が原点であるので、このTを実行することにより結果的には curPosに移動することになる (座標で表せば (curPos.x, curPos.y) へ移動することになる)。
図6 Code4 実行結果 Code3ではキーを1回1回押さなければ、Pointを動かすことはできない。ここでは、キーを押し続けることで、そのキーに対応する移動を連続して行うプログラムを作成する。
今回も、H、J、K、Lキーによって Pointを動かすが、各キーに対応する移動の方向はCode3と同じである。
Code3からの変更点は、Input.GetKeyDown(..) を連続押しに対応する Input.GetKey(..) に変更し、1回1回の移動量を $1$ から $0.05$ に変えるだけである。
実行結果(図6)に見られるように、キーの長押しに対応させているので Pointの移動が連続的なものになっている (キーの長押しによる連続的な移動の場合は、押し続けている限り毎フレーム移動が発生するので、1フレームあたりの移動量の設定には注意する必要がある)。
[Code4] (実行結果 図6)
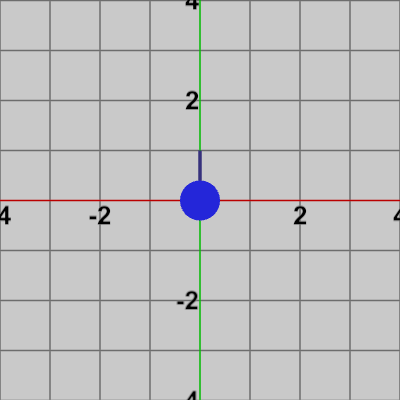
図7 Pointと進行線 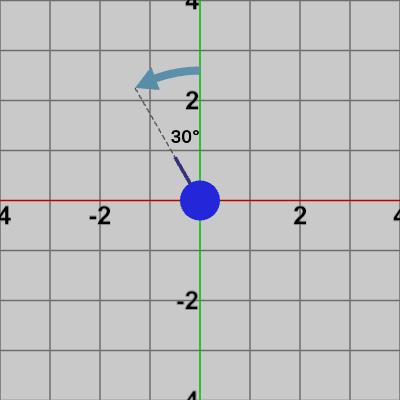
図8 30°回転した進行線
図7には Pointの他に、青色の細い線が Pointからy軸のプラス方向に出ている (今までの図よりも、やや拡大して表示してある)。この青色の細い線をここでは進行線と呼ぶことにする。この進行線は Pointの進む方向を表しており、次のインスタンス変数と重要な関わりがある。
進行線は初期の状態でy軸のプラス方向を向いている、すなわち 進行線の初期方向は $(0, 1)$ である。i_forwardDegree は進行線の現在の回転角度のことで、初期の方向である $(0, 1)$ から何度回転したかを表す (初期値は$0$)。例えば進行線が$30$°回転した状態は図8のようになる (このときの i_forwardDegreeの値は$30$である)。進行線は補助的な道具であり、今までのプログラムにおけるオブジェクトとは違ってプログラムから直接アクセスする必要はない。
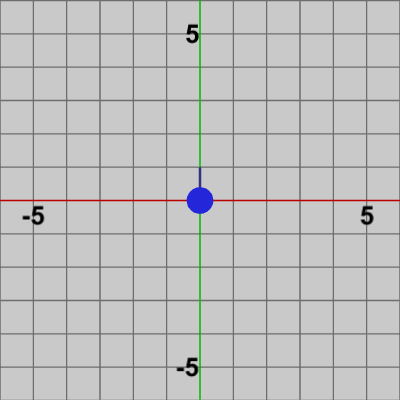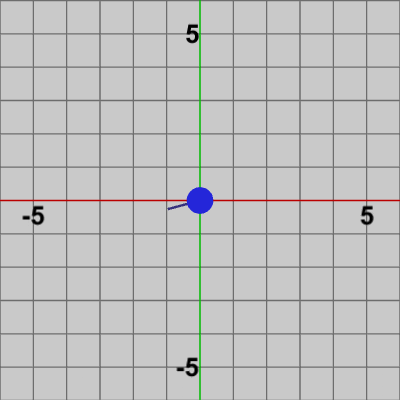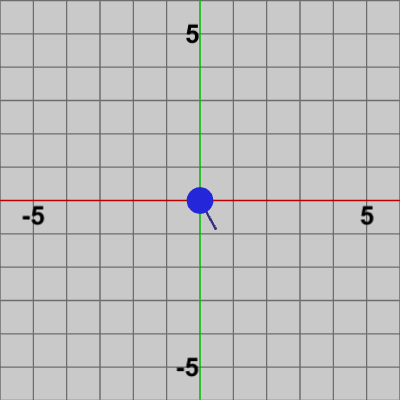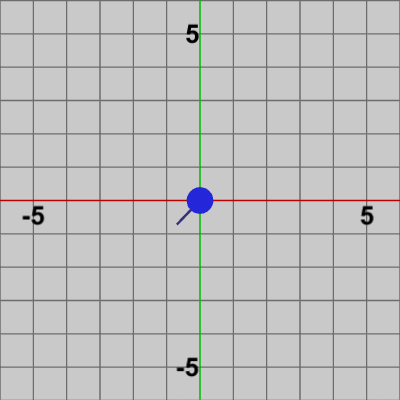
図9 Code5 実行結果 つまり、進行線を動かすために obj.SetMatrix(M) のような記述は必要ない。進行線は i_forwardDegree を更新すれば、その値に応じた回転を自動的に行う。
実際に、次のキー操作によって進行線を回転させてみよう。
H : 進行線が反時計周りに$1$°回転 (i_forwardDegreeに$1$を足す)。
L : 進行線が時計周りに$1$°回転 (i_forwardDegreeから$1$を引く)。
なお、これらの操作は Input.GetKey(..) を通して行うので長押しに対応する。
[Code5] (実行結果 図9)
11行目の forwardDir は進行線の現在の向きを表す Vector2型のローカル変数である。10行目で i_forwardDegreeだけ回転させる行列Rを取得する。11行目の計算は、進行線の初期方向である $(0, 1)$ を i_forwardDegreeだけ回転させて、回転後の方向を forwardDirにセットするものである (ただし、このプログラムでは計算結果がセットされるだけでそれ以降では使われない)。数式で表すと以下のようになる。\[forwardDir = R\begin{pmatrix}0 \\1 \\ 1\end{pmatrix}\] これは回転行列とベクトルの積を同次座標化して表したものである (1-6節参照)。プログラムや上の数式においても $(0, 1)$ の同次座標である $(0, 1, 1)$ が使われている。また、forwardDirは Vector2型、すなわち 2次元ベクトルであるが、$R$と $(0, 1, 1)$ の積は3次元ベクトルである。しかし、11行目において次のように記述されている。
こうした記述は今までにも何度か使われてきたが、これは計算結果である Vector3型の値を Vector2型の forwardDirにセットすることなるが、Unityではこういった記述は問題なく通る。この場合はVector3型のx座標、y座標のみが i_forwardDirectionにセットされ、z座標は切り捨てられる。
例えば、次のようなコードの場合は、
Unityでは、v3のx座標、y座標である $(1, 2)$ が、v2にセットされ、z座標の$3$は切り捨てられるのである(この事情は Vector3型と Vector4型の間でも成り立つ)。平行移動、回転、スケールを表す変換行列とベクトルの積を同次座標化して計算した結果は、2D空間の場合は3次元ベクトルであるが、この計算結果を2次元ベクトルに戻す際にはこういった自動的な切り捨ては効率的なのである。
$(0, 1)$ は大きさ$1$の単位ベクトルであり、それを回転させた結果も大きさ$1$の単位ベクトルであるから、forwardDirは常に単位ベクトルである。進行線の大きさも$1$であり(図7)、forwardDirは進行線の現在の方向を表すから、進行線は forwardDirを可視化したものであるといえる。
このプログラムでは、Pointは初期状態のまま動かさないので14行目で
となっている。
次のキー操作を追加する。
S : Pointを進行線の方向に一定の距離だけ移動させる(長押し非対応)。
1-3節で見たように、ある方向に、指定された距離だけ移動させる場合には単位ベクトルを使う。
例えば点$P$を、単位ベクトル$\boldsymbol{u}$が示す方向に、距離$d$だけ移動させる場合の位置は次のように求められる(移動後の位置を$P'$とする)。\[ P + d\boldsymbol{u} = P'\]
ここで移動の対象となっているのはPointであるが、Code3、Code4においては Pointの位置はローカル変数curPosによって表されていた。また、Code5では進行線の方向は単位ベクトル forwardDirによって表されていた。この2つの変数を使用した場合には、Pointを進行線の方向に距離$d$だけ移動させる計算は以下のようになる(移動後の位置を $newPos$ とする)。\[ curPos + d*forwardDir = newPos \]この計算は以下のプログラムの18行目で行われている (ただし $newPos$という変数は使われてはいない)。
では実際のプログラムを見てみよう。
[Code6] (実行結果 図10, 図11)
1行目で現在位置を取得していることを除けば、このプログラムの13行目まではCode5と特に変わるところはない。15行目から19行目の ifブロックは Sキーが押されたときのみ処理される。このブロックでは18行目において、現在の位置から進行線の方向に距離dだけ移動した位置を計算し、curPosを更新する。Sキーが押されければ、この ifブロックに入ることはないので curPosの更新も行われず、したがって Pointの位置は変化しない。
21行目で curPosに移動する平行移動行列Tを取得し、Pointに実行する。
以下の2つの図は、このプログラムの実行結果であるが、Sキーを押した際の Pointの移動距離を表す変数dを、左側は d = 0.5、右側は d = 1.0にした場合である。左の図では Pointは$0.5$ずつ移動しており、右の図では$1$ずつ移動している。

図10 Code6 実行結果 (d = 0.5) 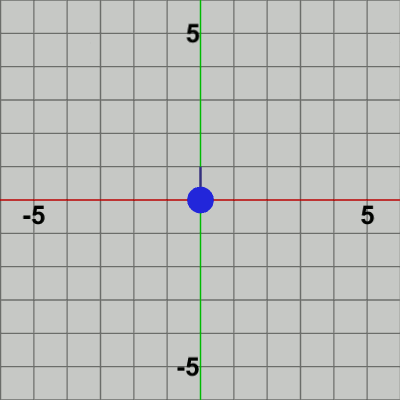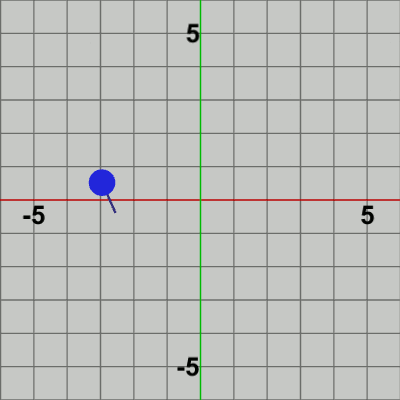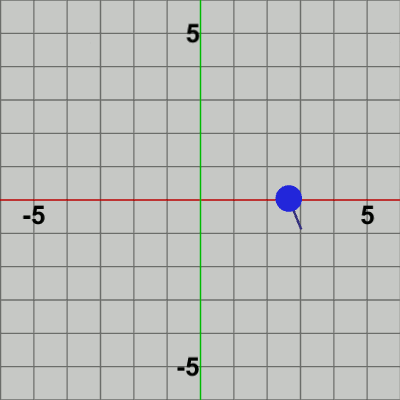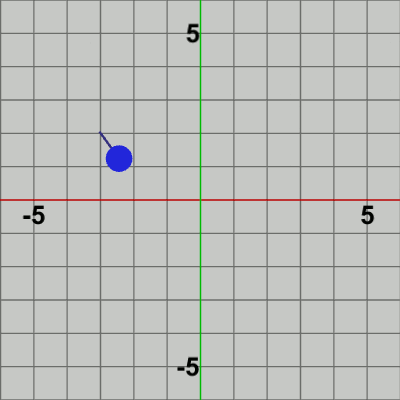
図11 Code6 実行結果 (d = 1.0)
しかし、Code6からの変更点はほとんどない。Sキーの長押しに対応させるために、Input.GetKeyDown(..) をInput.GetKey(..) に変更することと、1回あたりの移動量を表す変数dの値をもっと小さな値にすることである。
ただ1点、このプログラムではSキーが押されたときの記述を前回のプログラムとは変えてある。Code6では Sキーが押されたときの処理は、次のように ifブロックで記述されていた。
この ifブロックによる記述を三項演算子を使用して次のように表すことができる。
三項演算子を使用した場合も処理内容は同じである。Sキーが押されていれば curPosから forwardDirの方向へ dだけ進んだ位置を返し、押されていなければ curPosを返す (つまり、押されていない場合の位置の変化はない)。
この三項演算子による変更は、あくまでプログラムの'見た目'に関するものであり、本質的に必要なものではない (ただし、この記述は後のプログラムでも多用されるのでしっかりと理解しておいてほしい)。
実際のプログラムは以下のようになる。
[Code7] (実行結果 図12, 図13)
実行結果を図12、図13に示す。
図12では1回あたりの移動量を表す変数dの値が d = 0.03、図13では d = 0.12である。連続的な移動の場合は、1回あたりの移動量を少しでも大きくすると図13のように、運動が'かなり'速くなってしまうのである。

図12 Code7 実行結果 (d = 0.03) 
図13 Code7 実行結果 (d = 0.12)
# Code1
しかし、まずその前にUnityにおける基本的なキー操作の実装を簡単に解説する。何らかのキーを押した際には、次のメソッドがtrueを返す。
Input.GetKeyDown(KeyCode.#)
アルファベットを押したかどうかを判定するには引数の#の部分にAからZのアルファベットを指定する。キーボードの数字(テンキーではなく)を押したかどうかを判定するには#の部分にAlpha0からAlpha9を指定する。
例えば、Aを押したかどうかの判定は、
if(Input.GetKeyDown(KeyCode.A)){ ... }
キーボードの1を押したかどうかの判定は、
if(Input.GetKeyDown(KeyCode.Alpha1)){ ... }
次のプログラムはアルファベットのH、J、K、L、数字の1、2、3が押された際に該当するif文の中身が実行される(Unityのコンソール上に "PRESSED : #" と表示される)。
[Code1] (実行結果 図1)
if (Input.GetKeyDown(KeyCode.H))
{
Debug.Log("PRESSED : H");
}
else if (Input.GetKeyDown(KeyCode.J))
{
Debug.Log("PRESSED : J");
}
else if (Input.GetKeyDown(KeyCode.K))
{
Debug.Log("PRESSED : K");
}
else if (Input.GetKeyDown(KeyCode.L))
{
Debug.Log("PRESSED : L");
}
else if (Input.GetKeyDown(KeyCode.Alpha1))
{
Debug.Log("PRESSED : 1");
}
else if (Input.GetKeyDown(KeyCode.Alpha2))
{
Debug.Log("PRESSED : 2");
}
else if (Input.GetKeyDown(KeyCode.Alpha3))
{
Debug.Log("PRESSED : 3");
}
実行結果を図1に示す。

# Code2
Input.GetKeyDown(KeyCode.#)は、キーを押した際にはtrueを返すが、キーを押し続けている状態で返されるのはfalseである。つまり、あるキーが押しっぱなしであるかどうかを判定する場合には使うことができない。キーを押し続けているかどうかの判定には次のメソッドを使用する。何らかのキーを押し続けている状態であるとき、次のメソッドがtrueを返す。
Input.GetKey(KeyCode.#)
例えば、Aを押し続けているかどうかの判定は、
if(Input.GetKey(KeyCode.A)){ ... }
次のプログラムはアルファベットのH、J、K、Lを押し続けている状態において該当するif文の中身が実行される(Unityのコンソール上に連続して "pressing : #" と表示される)。
[Code2] (実行結果 図2)
if (Input.GetKey(KeyCode.H))
{
Debug.Log("pressing : H");
}
else if (Input.GetKey(KeyCode.J))
{
Debug.Log("pressing : J");
}
else if (Input.GetKey(KeyCode.K))
{
Debug.Log("pressing : K");
}
else if (Input.GetKey(KeyCode.L))
{
Debug.Log("pressing : L");
}
実行結果を図2に示す。

最後に、プログラム実行後から何フレーム目であるかをカウントするint型インスタンス変数 i_frameCount を使って、この2つのメソッドの動作を確認しよう (i_frameCountの初期値は $0$)。
[Beta2] (実行結果 図3)
i_frameCount++;
if (Input.GetKeyDown(KeyCode.A))
{
Debug.Log("PRESSED : A ("+i_frameCount+")");
}
if (Input.GetKey(KeyCode.A))
{
Debug.Log("pressing : A ("+i_frameCount+")");
}

図では分かりずらいが、Unityのコンソール画面上の表示結果を要約すると以下のようになる。
PRESSED : A (267)
pressing : A (267)
pressing : A (268)
pressing : A (269)
... ...
pressing : A (287)
pressing : A (288)
この結果の意味することは、「プログラム実行後の267フレーム目で、Aキーが押されたことが2つのメソッドInput.GetKeyDown(..)、Input.GetKey(..)によって検出された。その後の288フレーム目までAキーは押され続けていた。」ということである。
Input.GetKeyDown(..)は押されたフレームにおいてのみtrueを返し、Input.GetKey(..)は押されたフレーム、及びその後押され続けている間のフレームにおいてtrueを返すのである。
# Code3
ここから本題に戻る。図4は、オブジェクトPointの初期状態である。この Pointを、指定したキーを押すことによって上下左右に移動させるプログラムを作成しよう。


次のキー操作を実装する。
H : x軸方向に$-1$移動(左に$1$移動)
J : y軸方向に$-1$移動(下に$1$移動)
K : y軸方向に$+1$移動(上に$1$移動)
L : x軸方向に$+1$移動(右に$1$移動)
(Pointの移動量は、いずれのキーの場合でも$1$ずつの移動となる)
また、カスタムライブラリからオブジェクトの現在位置を取得するためのメソッドして次のメソッドを利用する。
// オブジェクトの現在の位置を取得 (戻り値は Vector2型) Vector2 GetPosition()
手順は次の通り。
(1) Pointの現在位置を取得し、ローカル変数curPosへセット (プログラム1行目 ; Pointの初期位置は原点であるので、プログラム実行後の最初の GetPosition() の戻り値は(0, 0)である)。
(2) 押されたキーに対応する移動を curPos に加算して、現在の位置を表すデータを更新(3~18行目)。
(3) curPosだけ移動する行列を取得して、Pointに実行する(20~21行目)。
[Code3] (実行結果 図5)
Vector2 curPos = Point.GetPosition();
if (Input.GetKeyDown(KeyCode.H))
{
curPos.x -= 1.0f;
}
else if (Input.GetKeyDown(KeyCode.J))
{
curPos.y -= 1.0f;
}
else if (Input.GetKeyDown(KeyCode.K))
{
curPos.y += 1.0f;
}
else if (Input.GetKeyDown(KeyCode.L))
{
curPos.x += 1.0f;
}
THMatrix3x3 T = TH2DMath.GetTranslation3x3(curPos);
Point.SetMatrix(T);
20行目で算出される平行移動行列Tは、curPosだけの平行移動を行うものであるが、Pointの場合は初期状態の位置が原点であるので、このTを実行することにより結果的には curPosに移動することになる (座標で表せば (curPos.x, curPos.y) へ移動することになる)。
# Code4

今回も、H、J、K、Lキーによって Pointを動かすが、各キーに対応する移動の方向はCode3と同じである。
Code3からの変更点は、Input.GetKeyDown(..) を連続押しに対応する Input.GetKey(..) に変更し、1回1回の移動量を $1$ から $0.05$ に変えるだけである。
実行結果(図6)に見られるように、キーの長押しに対応させているので Pointの移動が連続的なものになっている (キーの長押しによる連続的な移動の場合は、押し続けている限り毎フレーム移動が発生するので、1フレームあたりの移動量の設定には注意する必要がある)。
[Code4] (実行結果 図6)
Vector2 curPos = Point.GetPosition();
if (Input.GetKey(KeyCode.H))
{
curPos.x -= 0.05f;
}
else if (Input.GetKey(KeyCode.L))
{
curPos.x += 0.05f;
}
if (Input.GetKey(KeyCode.J))
{
curPos.y -= 0.05f;
}
else if (Input.GetKey(KeyCode.K))
{
curPos.y += 0.05f;
}
THMatrix3x3 T = TH2DMath.GetTranslation3x3(curPos);
Point.SetMatrix(T);
# Code5
次に、オブジェクト Pointが上下左右だけでなく、$360$°任意の方向に移動できるプログラムを作成しよう。そのために補助的な道具をここで用意する。

図7には Pointの他に、青色の細い線が Pointからy軸のプラス方向に出ている (今までの図よりも、やや拡大して表示してある)。この青色の細い線をここでは進行線と呼ぶことにする。この進行線は Pointの進む方向を表しており、次のインスタンス変数と重要な関わりがある。
// 進行線の現在の回転角度 (y軸プラス方向から何度回転しているか) int i_forwardDegree = 0;

実際に、次のキー操作によって進行線を回転させてみよう。
H : 進行線が反時計周りに$1$°回転 (i_forwardDegreeに$1$を足す)。
L : 進行線が時計周りに$1$°回転 (i_forwardDegreeから$1$を引く)。
なお、これらの操作は Input.GetKey(..) を通して行うので長押しに対応する。
[Code5] (実行結果 図9)
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 1;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Point.SetMatrix(THMatrix3x3.identity);
11行目の forwardDir は進行線の現在の向きを表す Vector2型のローカル変数である。10行目で i_forwardDegreeだけ回転させる行列Rを取得する。11行目の計算は、進行線の初期方向である $(0, 1)$ を i_forwardDegreeだけ回転させて、回転後の方向を forwardDirにセットするものである (ただし、このプログラムでは計算結果がセットされるだけでそれ以降では使われない)。数式で表すと以下のようになる。\[forwardDir = R\begin{pmatrix}0 \\1 \\ 1\end{pmatrix}\] これは回転行列とベクトルの積を同次座標化して表したものである (1-6節参照)。プログラムや上の数式においても $(0, 1)$ の同次座標である $(0, 1, 1)$ が使われている。また、forwardDirは Vector2型、すなわち 2次元ベクトルであるが、$R$と $(0, 1, 1)$ の積は3次元ベクトルである。しかし、11行目において次のように記述されている。
Vector2 forwardDir = R * new Vector3(0, 1, 1);
例えば、次のようなコードの場合は、
Vector3 v3 = new Vector3(1, 2, 3); Vector2 v2 = v3;
$(0, 1)$ は大きさ$1$の単位ベクトルであり、それを回転させた結果も大きさ$1$の単位ベクトルであるから、forwardDirは常に単位ベクトルである。進行線の大きさも$1$であり(図7)、forwardDirは進行線の現在の方向を表すから、進行線は forwardDirを可視化したものであるといえる。
このプログラムでは、Pointは初期状態のまま動かさないので14行目で
Point.SetMatrix(THMatrix3x3.identity);
# Code6
では実際に Pointを進行線の方向に動かしてみよう。次のキー操作を追加する。
S : Pointを進行線の方向に一定の距離だけ移動させる(長押し非対応)。
1-3節で見たように、ある方向に、指定された距離だけ移動させる場合には単位ベクトルを使う。
例えば点$P$を、単位ベクトル$\boldsymbol{u}$が示す方向に、距離$d$だけ移動させる場合の位置は次のように求められる(移動後の位置を$P'$とする)。\[ P + d\boldsymbol{u} = P'\]
ここで移動の対象となっているのはPointであるが、Code3、Code4においては Pointの位置はローカル変数curPosによって表されていた。また、Code5では進行線の方向は単位ベクトル forwardDirによって表されていた。この2つの変数を使用した場合には、Pointを進行線の方向に距離$d$だけ移動させる計算は以下のようになる(移動後の位置を $newPos$ とする)。\[ curPos + d*forwardDir = newPos \]この計算は以下のプログラムの18行目で行われている (ただし $newPos$という変数は使われてはいない)。
では実際のプログラムを見てみよう。
[Code6] (実行結果 図10, 図11)
Vector2 curPos = Point.GetPosition();
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
if (Input.GetKeyDown(KeyCode.S))
{
float d = 0.5f;
curPos += d * forwardDir;
}
THMatrix3x3 T = TH2DMath.GetTranslation3x3(curPos);
Point.SetMatrix(T);
1行目で現在位置を取得していることを除けば、このプログラムの13行目まではCode5と特に変わるところはない。15行目から19行目の ifブロックは Sキーが押されたときのみ処理される。このブロックでは18行目において、現在の位置から進行線の方向に距離dだけ移動した位置を計算し、curPosを更新する。Sキーが押されければ、この ifブロックに入ることはないので curPosの更新も行われず、したがって Pointの位置は変化しない。
21行目で curPosに移動する平行移動行列Tを取得し、Pointに実行する。
以下の2つの図は、このプログラムの実行結果であるが、Sキーを押した際の Pointの移動距離を表す変数dを、左側は d = 0.5、右側は d = 1.0にした場合である。左の図では Pointは$0.5$ずつ移動しており、右の図では$1$ずつ移動している。


# Code7
Code6では Pointを移動させるためには、Sキーを1回1回押さなければならなかった。今回は、それを変更してSキーを押し続けることによって、Pointが連続的に移動できるようにしてみよう。しかし、Code6からの変更点はほとんどない。Sキーの長押しに対応させるために、Input.GetKeyDown(..) をInput.GetKey(..) に変更することと、1回あたりの移動量を表す変数dの値をもっと小さな値にすることである。
ただ1点、このプログラムではSキーが押されたときの記述を前回のプログラムとは変えてある。Code6では Sキーが押されたときの処理は、次のように ifブロックで記述されていた。
if (Input.GetKeyDown(KeyCode.S))
{
float d = 0.5f;
curPos += d * forwardDir;
}
この ifブロックによる記述を三項演算子を使用して次のように表すことができる。
float d = 0.5f; Vector2 newPos = (Input.GetKeyDown(KeyCode.S)) ? curPos + d * forwardDir : curPos;
三項演算子を使用した場合も処理内容は同じである。Sキーが押されていれば curPosから forwardDirの方向へ dだけ進んだ位置を返し、押されていなければ curPosを返す (つまり、押されていない場合の位置の変化はない)。
この三項演算子による変更は、あくまでプログラムの'見た目'に関するものであり、本質的に必要なものではない (ただし、この記述は後のプログラムでも多用されるのでしっかりと理解しておいてほしい)。
実際のプログラムは以下のようになる。
[Code7] (実行結果 図12, 図13)
Vector2 curPos = Point.GetPosition();
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
float d = 0.03f;
Vector2 newPos = (Input.GetKey(KeyCode.S)) ? curPos + d * forwardDir : curPos;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newPos);
Point.SetMatrix(T);
実行結果を図12、図13に示す。
図12では1回あたりの移動量を表す変数dの値が d = 0.03、図13では d = 0.12である。連続的な移動の場合は、1回あたりの移動量を少しでも大きくすると図13のように、運動が'かなり'速くなってしまうのである。


© 2020-2025 Redpoll's 60 (All rights reserved)